Cara Alternatif Untuk Menghafal Nilai Sudut Istimewa Perbandingan Trigonometri

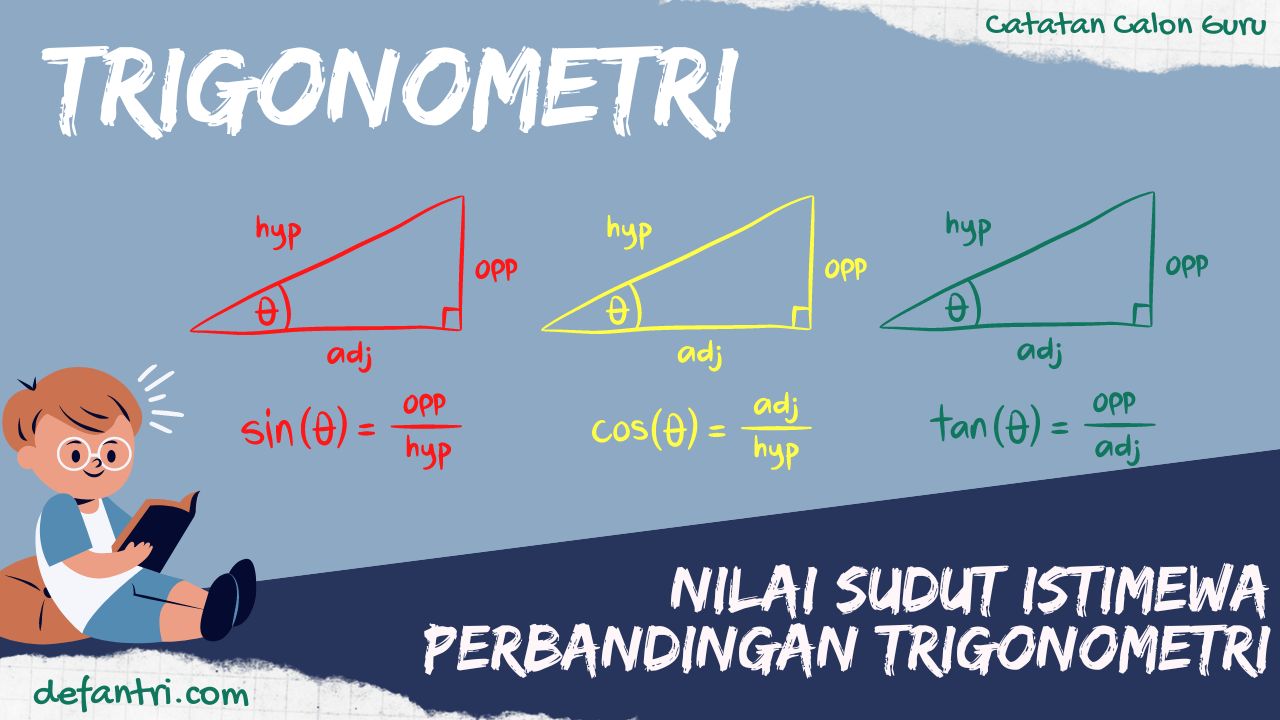
Catatan calon guru kali ini coba berdiskusi tentang Cara Alternatif dan Sangat Kreatif Untuk Menghafal Nilai Sudut -sudut Istimewa pada Perbandingan Trigonometri.

Sebelumnya kita sudah mengenal dan setidaknya tahu yang dimaksud dengan Perbandingan Trigonometri. Dalam mempelajari perbandingan trigonometri, kita tidak bisa lepas dari yang namanya sudut dan terkhusus sudut istimewa. Istilah sudut istimewa ini sering juga dikatakan dengan 'sudut khusus'.

Dikatakan sudut istimewa atau sudut khusus, karena sudut ini nilai perbandingan trigonometrinya dapat ditentukan tanpa menggunakan alat hitung seperti kalkulator atau tabel trigonometri.

Sebagai dasar, kita coba menghafal sudut istimewa perbandingan trigonometri untuk sudut $ 0^{\circ},\ 30^{\circ},\ 45^{\circ},\ 60^{\circ},\ dan\ 90^{\circ} $.

Jika sudah bisa mengingat sudut istimewa $ 0^{\circ},\ 30^{\circ},\ 45^{\circ},\ 60^{\circ},\ dan\ 90^{\circ} $ secara berurut dari yang terkecil sampai yang terbesar, maka nilai perbandingan trigonometri pada sudut-sudut ini dapat dengan mudah kita tentukan. Bagaimana cara menemukan nilainya mari kita mulai💗

Nilai Sudut Istimewa Untuk Sinus

Untuk menghafal nilai perbandingan trigonemetri pada sinus, coba perhatikan bilangan berikut:
$ \frac{1}{2}\sqrt{0}$, $\frac{1}{2}\sqrt{1},$ $\frac{1}{2}\sqrt{2},$ $\frac{1}{2}\sqrt{3},$ $\frac{1}{2}\sqrt{4}$
Bilangan di atas mempunyai pola yang berurut naik, dan bilangan di atas kita pindahkan pada tabel perbandingan trigonometri untuk sinus, menjadi seperti berikut ini:

Nilai Sudut Istimewa Sinus
$\alpha$	$0^{\circ}$	$30^{\circ}$	$45^{\circ}$	$60^{\circ}$	$90^{\circ}$
$sin\ \alpha$	$\frac{1}{2}\sqrt{0}$	$\frac{1}{2}\sqrt{1}$	$\frac{1}{2}\sqrt{2}$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{2}\sqrt{4}$
$sin\ \alpha$	$0$	$\frac{1}{2}$	$\frac{1}{2}\sqrt{2}$	$\frac{1}{2}\sqrt{3}$	$1$

Dari tabel di atas kita peroleh, $sin\ 0^{\circ} = 0$, $sin\ 30^{\circ} = \frac{1}{2}$, $sin\ 45^{\circ} = \frac{1}{2}\sqrt{2}$, $sin\ 60^{\circ} = \frac{1}{2}\sqrt{3}$, dan $sin\ 90^{\circ} = 1$.

Nilai Sudut Istimewa Untuk Cosinus

Untuk menghafal nilai perbandingan trigonemetri pada sinus, coba perhatikan bilangan berikut:
$ \frac{1}{2}\sqrt{4},$ $\frac{1}{2}\sqrt{3},$ $\frac{1}{2}\sqrt{2},$ $\frac{1}{2}\sqrt{1},$ $\frac{1}{2}\sqrt{0}$
Bilangan di atas mempunyai pola yang berurut turun, dan bilangan di atas kita pindahkan pada tabel perbandingan trigonometri untuk cosinus, menjadi seperti berikut ini:

Nilai Sudut Istimewa Cosinus
$\alpha$	$0^{\circ}$	$30^{\circ}$	$45^{\circ}$	$60^{\circ}$	$90^{\circ}$
$cos\ \alpha$	$\frac{1}{2}\sqrt{4}$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{2}\sqrt{2}$	$\frac{1}{2}\sqrt{1}$	$\frac{1}{2}\sqrt{0}$
$cos\ \alpha$	$1$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{2}\sqrt{2}$	$\frac{1}{2}$	$0$

Dari tabel di atas kita peroleh, $cos\ 0^{\circ} = 1$, $cos\ 30^{\circ} = \frac{1}{2}\sqrt{3}$, $cos\ 45^{\circ} = \frac{1}{2}\sqrt{2}$, $cos\ 60^{\circ} = \frac{1}{2} $, dan $cos\ 90^{\circ} = 0$.

Nilai Sudut Istimewa Untuk tangen

Untuk mengetahui nilai tan kita hanya perlu melakukan hitungan sederhana yaitu:

1. $ tan\ 0^{\circ} = \dfrac{sin\ 0^{\circ}}{cos\ 0^{\circ}}=\dfrac{0}{1}= 0 $
2. $ tan\ 30^{\circ} = \dfrac{sin\ 30^{\circ}}{cos\ 30^{\circ}}=\dfrac{\frac{1}{2}}{\frac{1}{2}\sqrt{3}}=\dfrac{1}{3}\sqrt{3}$
3. $ tan\ 45^{\circ}= \dfrac{sin\ 45^{\circ}}{cos\ 45^{\circ}} = \dfrac{\frac{1}{2}\sqrt{2}}{\frac{1}{2}\sqrt{2}}= 1 $
4. $ tan\ 60^{\circ}= \dfrac{sin\ 60^{\circ}}{cos\ 60^{\circ}} = \dfrac{\frac{1}{2}\sqrt{3}}{\frac{1}{2}}= \sqrt{3} $
5. $ tan\ 90^{\circ}= \dfrac{sin\ 90^{\circ}}{cos\ 90^{\circ}} = -\ \text{(tidak terdefenisi)}$

Setelah nilai $sin\ \alpha$, $cos\ \alpha$ dan $tan\ \alpha$ kita gabung dalam satu tabel menjadi seperti tabel berikut:

Nilai Trigonometri Sudut Istimewa
$\alpha$	$0^{\circ}$	$30^{\circ}$	$45^{\circ}$	$60^{\circ}$	$90^{\circ}$
$sin\ \alpha$	$0$	$\frac{1}{2}$	$\frac{1}{2}\sqrt{2}$	$\frac{1}{2}\sqrt{3}$	$1$
$cos\ \alpha$	$1$	$\frac{1}{2}\sqrt{3}$	$\frac{1}{2}\sqrt{2}$	$\frac{1}{2}$	$0$
$tan\ \alpha$	$0$	$\frac{1}{3}\sqrt{3}$	$1$	$\sqrt{3}$	$-$ (tidak terdefenisi)

Nilai perbandingan trigonometri sudut istimewa untuk cosecan, secan dan cotangen kita lakukan seperti mendapatkan nilai tangen, kita lakukan sedikit perhitungan.

• Menghitung nilai $cosecan\ \alpha$ dapat dihitung dengan $cosec\ \alpha= \dfrac{1}{sin\ \alpha}$.
  Misal $cosec\ 30^{\circ}= \dfrac{1}{sin\ 30^{\circ}}= \dfrac{1}{\dfrac{1}{2}}=2$
• Menghitung nilai $secan\ \alpha$ dapat dihitung dengan $sec\ \alpha= \dfrac{1}{cos\ \alpha}$.
  Misal $sec\ 45^{\circ}= \dfrac{1}{cos\ 45^{\circ}}= \dfrac{1}{\frac{1}{2}\sqrt{2}}=\sqrt{2}$
• Menghitung nilai $cotangen\ \alpha$ dapat dihitung dengan $cotan\ \alpha= \dfrac{1}{tan\ \alpha}$, atau $\dfrac{sin\ \alpha}{cos\ \alpha}$.
  Misal $cotan\ 60^{\circ}= \dfrac{1}{tan\ 60^{\circ}}= \dfrac{1}{\sqrt{3}}=\dfrac{1}{3}\sqrt{3}$

Nilai Perbandingan Trigonometri Untuk di Kuadran Dua, Tiga dan Empat

Untuk mengingat nilai perbandingan trigonometri pada kuadran dua, tiga dan empat dapat kita gunakan trik di atas.

Langkah-langkah diatas akan semakin mudah jika langsung dicoba, sebagai latihan kita lihat beberapa contoh soal berikut ini, selamat bermatematika🙏

1. Nilai dari $5 \cdot sin\ 45^{\circ} + 5 \cdot cos\ 30^{\circ} + 2 \cdot tan\ 60^{\circ}$ adalah...

Alternatif Pembahasan:

Show

$\begin{align}
& 5 \cdot sin\ 60^{\circ} + 4 \cdot cos\ 30^{\circ} + 2 \cdot tan\ 60^{\circ} \\
&=5 \cdot \dfrac{1}{2}\sqrt{3} + 4 \cdot \dfrac{1}{2}\sqrt{3} + 2 \cdot \sqrt{3} \\
&= \dfrac{5}{2}\sqrt{3} + 2 \sqrt{3} + 2 \sqrt{3} \\
&= \dfrac{5}{2}\sqrt{3} + 4 \sqrt{3} \\
&= \dfrac{5}{2}\sqrt{3} + \dfrac{8}{2}\sqrt{3} \\
&= \dfrac{13}{2}\sqrt{3}
\end{align}$

2. Nilai dari $6 \cdot sin\ 60^{\circ} \cdot 2 \cdot cos\ 45^{\circ} \cdot tan\ 45^{\circ}$ adalah...

Alternatif Pembahasan:

Show

$\begin{align}
& 6 \cdot sin\ 60^{\circ} \cdot 2 \cdot cos\ 45^{\circ} \cdot tan\ 45^{\circ} \\
&= 6 \cdot \dfrac{1}{2}\sqrt{3} \cdot 2 \cdot \dfrac{1}{2}\sqrt{2} \cdot 1 \\
&= 3 \sqrt{3} \cdot \sqrt{2} \cdot 1 \\
&= 3 \sqrt{3 \cdot 2} \\
&= 3 \sqrt{6}
\end{align}$

3. Nilai dari $6 \cdot sin\ 60^{\circ} \cdot 2 \cdot cos\ 45^{\circ} \cdot tan\ 45^{\circ}$ adalah...

Alternatif Pembahasan:

Show

$\begin{align}
& 4 \cdot sin\ 45^{\circ} + 2 \cdot \dfrac{cos\ 45^{\circ}}{tan\ 45^{\circ}} \\
&= 4 \cdot \dfrac{1}{2}\sqrt{2} + 2 \cdot \dfrac{\dfrac{1}{2}\sqrt{2}}{1} \\
&= 2 \sqrt{2} + 2 \cdot \dfrac{1}{2}\sqrt{2} \\
&= 2 \sqrt{2} + \sqrt{2} \\
&= 3 \sqrt{2}
\end{align}$

4. Hitunglah nilai dari $\dfrac{cos\ 30^{\circ} + sin\ 45^{\circ}}{sec\ 0^{\circ}}=\cdots$

Alternatif Pembahasan:

Show

$\begin{align}
& \dfrac{cos\ 30^{\circ} + sin\ 45^{\circ}}{sec\ 0^{\circ}} \\
&= \dfrac{\dfrac{1}{2}\sqrt{3} + \dfrac{1}{2}\sqrt{2}}{\dfrac{1}{cos\ 0^{\circ}}} \\
&= \dfrac{\dfrac{1}{2}\sqrt{3} + \dfrac{1}{2}\sqrt{2}}{\dfrac{1}{1}} \\
&= \dfrac{\dfrac{1}{2}\sqrt{3} + \dfrac{1}{2}\sqrt{2}}{1} \\
&= \dfrac{1}{2}\sqrt{3} + \dfrac{1}{2}\sqrt{2} \\
&= \dfrac{1}{2} \left( \sqrt{3} + \sqrt{2} \right)
\end{align}$

5. Tentukan nilai dari $sin\ 150^{\circ} \cdot cos\ 225^{\circ} \cdot tan\ 300^{\circ}=\cdots$

Alternatif Pembahasan:

Show

#$\begin{align}
sin\ 150^{\circ} &= sin\ \left( 180^{\circ}-30^{\circ} \right) \\
&= sin\ 30^{\circ} = \dfrac{1}{2}\\
\hline
sin\ 150^{\circ} &= sin\ \left( 90^{\circ}+60^{\circ} \right) \\
&= cos\ 30^{\circ} = \dfrac{1}{2}\\
\end{align}$

#$\begin{align}
cos\ 225^{\circ} &= cos\ \left( 180^{\circ}+45^{\circ} \right) \\
&=- cos\ 45^{\circ} = -\dfrac{1}{2}\sqrt{2}\\
\hline
cos\ 225^{\circ} &= cos\ \left( 270^{\circ}-45^{\circ} \right) \\
&=- sin\ 45^{\circ} = -\dfrac{1}{2}\sqrt{2}\\
\end{align}$

#$\begin{align}
tan\ 300^{\circ} &= tan\ \left( 360^{\circ}-60^{\circ} \right) \\
&=- tan\ 60^{\circ} = - \sqrt{3}\\
\hline
tan\ 300^{\circ} &= tan\ \left( 270^{\circ}+30^{\circ} \right) \\
&=- cotan\ 30^{\circ} = -\sqrt{3}\\
\end{align}$

$\begin{align}
& sin\ 150^{\circ} \cdot cos\ 225^{\circ} \cdot tan\ 300^{\circ} \\
&= \left(\dfrac{1}{2}\right) \left( -\dfrac{1}{2}\sqrt{2} \right)\left(-\sqrt{3}\right) \\
&= \dfrac{1}{4} \sqrt{6}
\end{align}$

6. Hitunglah nilai dari sudut $(a).\ sin\ 120^{\circ}$, $(b).\ cos\ 135^{\circ}$, $(c).\ sin\ 240^{\circ}$, $(d).\ tan\ 150^{\circ}$, $(e).\ cos\ 315^{\circ}$, $(f).\ tan\ 330^{\circ}$, $(g).\ sec\ 210^{\circ}$, $(h).\ cot\ 120^{\circ}$, $(i).\ cos\ -60^{\circ}$

Alternatif Pembahasan:

Show

$(a).$ Sudut $120^{\circ}$ berada pada kuadran kedua sehingga $sin\ 120^{\circ}$ dapat kita pastikan bernilai positif.
$\begin{align}
sin\ 120^{\circ} &= sin\ \left( 90^{\circ}+30^{\circ} \right) \\
&= cos\ 30^{\circ} = \dfrac{1}{2}\sqrt{3} \\
\hline
sin\ 120^{\circ} &= sin\ \left( 180^{\circ}-60^{\circ} \right) \\
&= sin\ 60^{\circ} = \dfrac{1}{2}\sqrt{3}
\end{align}$

$(b).$ Sudut $135^{\circ}$ berada pada kuadran kedua sehingga $cos\ 135^{\circ}$ dapat kita pastikan bernilai negatif.
$\begin{align}
cos\ 135^{\circ} &= cos\ \left( 90^{\circ}+45^{\circ} \right) \\
&= -sin\ 45^{\circ} = -\dfrac{1}{2}\sqrt{2} \\
\hline
cos\ 135^{\circ} &= cos\ \left( 180^{\circ}-45^{\circ} \right) \\
&= -sin\ 45^{\circ} = -\dfrac{1}{2}\sqrt{2}
\end{align}$

$(c).$ Sudut $240^{\circ}$ berada pada kuadran ketiga sehingga $sin\ 240^{\circ}$ dapat kita pastikan bernilai negatif.
$\begin{align}
sin\ 240^{\circ} &= sin\ \left( 180^{\circ}+60^{\circ} \right) \\
&= -sin\ 60^{\circ} = -\dfrac{1}{2}\sqrt{3} \\
\hline
sin\ 240^{\circ} &= sin\ \left( 270^{\circ}-30^{\circ} \right) \\
&= -cos\ 30^{\circ} = -\dfrac{1}{2}\sqrt{3}
\end{align}$

$(d).$ Sudut $150^{\circ}$ berada pada kuadran kedua sehingga $tan\ 150^{\circ}$ dapat kita pastikan bernilai negatif.
$\begin{align}
tan\ 150^{\circ} &= tan\ \left( 90^{\circ}+60^{\circ} \right) \\
&=- cotan\ 60^{\circ} = - \dfrac{1}{3}\sqrt{3} \\
\hline
tan\ 150^{\circ} &= tan\ \left( 180^{\circ}-30^{\circ} \right) \\
&=- tan\ 30^{\circ} = \dfrac{1}{3}\sqrt{3}
\end{align}$

$(e).$ Sudut $315^{\circ}$ berada pada kuadran keempat sehingga $cos\ 315^{\circ}$ dapat kita pastikan bernilai positif.
$\begin{align}
cos\ 315^{\circ} &= cos\ \left( 270^{\circ}+45^{\circ} \right) \\
&= sin\ 45^{\circ} = \dfrac{1}{2}\sqrt{2} \\
\hline
cos\ 315^{\circ} &= cos\ \left( 360^{\circ}-45^{\circ} \right) \\
&= cos\ 45^{\circ} = \dfrac{1}{2}\sqrt{2}
\end{align}$

$(f).$ Sudut $330^{\circ}$ berada pada kuadran keempat sehingga $tan\ 330^{\circ}$ dapat kita pastikan bernilai negatif.
$\begin{align}
tan\ 330^{\circ} &= tan\ \left( 270^{\circ}+60^{\circ} \right) \\
&= -cot\ 60^{\circ} = -\dfrac{1}{3}\sqrt{3} \\
\hline
tan\ 330^{\circ} &= tan\ \left( 360^{\circ}-30^{\circ} \right) \\
&= tan\ 30^{\circ} = -\dfrac{1}{3}\sqrt{3}
\end{align}$

$(g).$ Sudut $210^{\circ}$ berada pada kuadran ketiga sehingga $sec\ 210^{\circ}$ dapat kita pastikan bernilai negatif.
$\begin{align}
sec\ 210^{\circ} &= sec\ \left( 180^{\circ}+30^{\circ} \right) \\
&= - sec\ 30^{\circ} = - \dfrac{1}{cos\ 30^{\circ}} \\
&= - \dfrac{1}{\dfrac{1}{2}\sqrt{3}} = - \dfrac{2}{3}\sqrt{3} \\
\hline
sec\ 210^{\circ} &= sec\ \left( 270^{\circ}-60^{\circ} \right) \\
&= - cosec\ 60^{\circ} = - \dfrac{1}{sin\ 60^{\circ}} \\
&= - \dfrac{1}{\dfrac{1}{2}\sqrt{3}} = - \dfrac{2}{3}\sqrt{3} \\
\end{align}$

$(h).$ Sudut $120^{\circ}$ berada pada kuadran kedua sehingga $cot\ 120^{\circ}$ dapat kita pastikan bernilai negatif.
$\begin{align}
cot\ 120^{\circ} &= cot\ \left( 90^{\circ}+30^{\circ} \right) \\
&= - tan\ 30^{\circ} = - \dfrac{1}{3}\sqrt{3} \\
\hline
cot\ 120^{\circ} &= cot\ \left( 180^{\circ}-60^{\circ} \right) \\
&= - cot\ 60^{\circ} = - \dfrac{1}{3}\sqrt{3} \\
\end{align}$

$(i).$ Sudut $-60^{\circ}$ sebenarnya adalah $360^{\circ}-60^{\circ}=300^{\circ}$ sehingga berada pada kuadran keempat sehingga $cos\ -60^{\circ}=cos\ 300^{\circ}$ dapat kita pastikan bernilai positif.
$\begin{align}
cos\ -60^{\circ} &= cos\ \left( 0^{\circ}-60^{\circ} \right) \\
&= cos\ 60^{\circ} = \dfrac{1}{2} \\
\hline
cos\ 300^{\circ} &= cos\ \left( 360^{\circ}-60^{\circ} \right) \\
&= cos\ 60^{\circ} = \dfrac{1}{2} \\
\hline
cos\ 300^{\circ} &= cos\ \left( 270^{\circ}+30^{\circ} \right) \\
&= sin\ 30^{\circ} = \dfrac{1}{2} \\
\end{align}$

7. Seorang anak berdiri $20$ meter dari sebuah tiang seperti gambar berikut,

Perkirakan ketinggian tiang dari titik $A$. Apabila diperlukan gunakan nilai pendekatan $\sqrt{2}=1,4$ dan $\sqrt{3}=1,7$.

Alternatif Pembahasan:

Show

Dari informasi pada gambar dan $tan\ 60^{\circ}$ dapat kita simpulkan:
$\begin{aligned}
tan\ 60^{circ} &= \dfrac{AB}{20} \quad && \left[ \dfrac{de}{sa} \right] \\
\sqrt{3} &= \dfrac{AB}{20} \\
1,7 \cdot 20 &= AB \\
34 &= AB
\end{aligned}$

$\therefore$ Tinggi tiang dari titik $A$ adalah $34\ m$

8. Diketahui titik $A$ tepat pada pohon cemara, dan pohon cemara dilihat dari titik $B$ yang berjarak $20$ dengan sudut elevasi $30^{\circ}$, ilustrasinya seperi gambar berikut:

Jika pohon cemara membentuk sudut $90^{\circ}$ dengan tanah, tentukan tingg pohon cemara...

Alternatif Pembahasan:

Show

Dari informasi pada gambar dan $tan\ 30^{\circ}$ dapat kita simpulkan:
$\begin{aligned}
tan\ 30^{circ} &= \dfrac{\text{tingggi pohon}}{20} \quad && \left[ \dfrac{de}{sa} \right] \\
\dfrac{1}{3}\sqrt{3} &= \dfrac{\text{tingggi pohon}}{20} \\
\dfrac{1}{3}\sqrt{3} \cdot 20 &= tingggi pohon \\
\dfrac{20}{3}\sqrt{3} &= tingggi pohon
\end{aligned}$

9. Diberikan sebuah segitiga sama sisi $ABC$ seperti gambar berikut:

Jika panjang TC adalah $12\ cm$, maka panjang sisi segitiga tersebut adalah...

Alternatif Pembahasan:

Show

Segitiga $ABC$ adalah sama sisi sehingga besar ketiga sudutnya adalah $60^{\circ}$, sehingga dapat kita simpulkan:
$\begin{aligned}
tan\ 60^{circ} &= \dfrac{CT}{BT} \quad && \left[ \dfrac{de}{sa} \right] \\
\sqrt{3} &= \dfrac{12}{BT} \\
BT &= \dfrac{12}{\sqrt{3}} \\
BT &= 4 \sqrt{3}
\end{aligned}$
Segitiga $ABC$ adalah sama sisi, $CT$ yang merupakan garis tinggi pada $AB$ juga merupakan garis berat sehingga $AT=TB$.

Panjang sisi segitiga $ABC$ adalah:
$\begin{aligned}
AB &= AT+TB \\
&= 4 \sqrt{3}+4 \sqrt{3} \\
&= 8 \sqrt{3}
\end{aligned}$

10. Perhatikan trapesium sama kaki berikut ini:

Hitunglah panjang $CD$

Alternatif Pembahasan:

Show

Trapesium coba kita gambarkan menjadi seperti berikut ini:

Dari gambar di atas, kita peroleh $sin\ 30^{\circ}$ dan $AB=2x+CD$:
$\begin{aligned}
sin\ 30^{circ} &= \dfrac{x}{10} \quad && \left[ \dfrac{de}{mi} \right] \\
\dfrac{1}{2} &= \dfrac{x}{10} \\
x &= 5
\end{aligned}$

Untuk $x=5$ dimana $AB=2x+CD$ maka $18=CD+2(5)$ atau $CD=8$.

Saran, Kritik atau Masukan yang sifatnya membangun terkait Cara Alternatif Untuk Menghafal Nilai Sudut Istimewa Perbandingan Trigonometri silahkan disampaikan😊CMIIW

Jangan Lupa Untuk Berbagi 🙏Share is Caring 👀 dan JADIKAN HARI INI LUAR BIASA! - WITH GOD ALL THINGS ARE POSSIBLE😊

Video pilihan khusus untuk Anda 💗 Cara Cepat Menghafal Menghafal Nilai Sudut Istimewa Perbandingan Trigonometri;