Belajar matematika bukanlah permainan anak-anak dan bukan suatu hal yang mudah. Ini adalah tugas yang menakutkan terutama ketika menyangkut integrasi pembelajaran. kalkulator integral dengan langkah-langkah sangat penting dan membantu meningkatkan pengetahuan siswa sambil mempelajari integrasi. Anda mengetahui berbagai langkah yang terlibat dalam proses integrasi. Integral merupakan salah satu konsep matematika yang krusial dan wajib dipelajari oleh mahasiswa teknik.
Pada artikel ini, kita membahas apa itu integral dan pentingnya integral.
Apa itu Integral?
Integrasi dan fungsi integral terbukti menjadi operasi fundamental. Kalkulator integral kompleks membantu memecahkan pemecah masalah matematika dan fisika dalam waktu singkat.
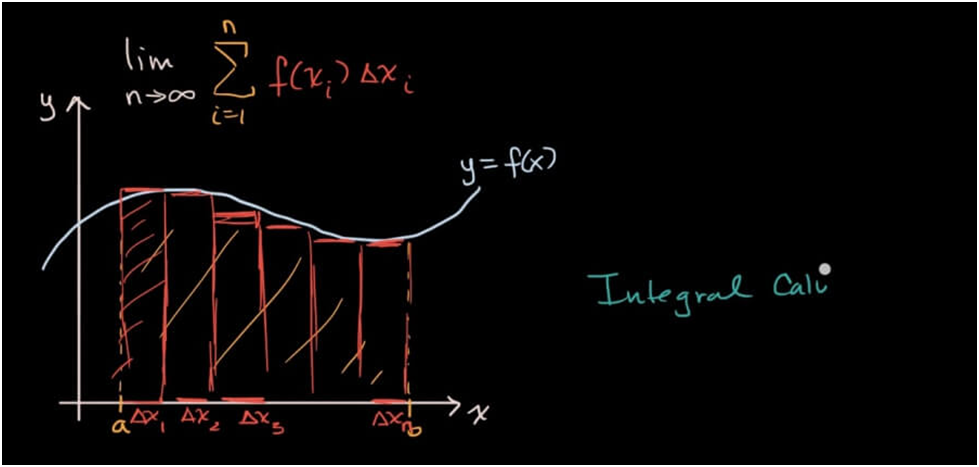
Contoh praktis:
Mari kita perhatikan integral tertentu dari $\int \limits_{2}^{3} x^{3}\ dx$,
integral di atas adalah integral dari $x^{3}$ dengan batas atas $x=3$ dan batas bawah $x=2$.
$ \begin{align} \int \limits_{2}^{3} x^{3}\ dx & = \left [\frac{1}{3+1}x^{3+1} \right ]_{2}^{3} \\ & = \left [\frac{1}{4}x^{4} \right ]_{2}^{3} \\ & = \left [\frac{1}{4}(3)^{4} \right ] - \left [\frac{1}{4}(2)^{4} \right ] \\ & = \left [\frac{1}{4}(81) \right ] - \left [\frac{1}{4}(16) \right ] \\ & = \frac{81}{4}- \frac{16}{4} \\ & = \frac{65}{4} \end{align} $
(Kalkulator Integral) menyelesaikan integral tertentu dan integral tak tentu. Siswa dapat mempelajari kedua jenis integral yang melibatkan perbandingan aljabar dan trigonometri seperti Sin, Cos, Tan, dll.
Bagaimana cara menyelesaikan integral?
- Langkah-langkah yang dilakukan dalam menyelesaikan integral adalah:
- Menyelesaikan integral adalah penentuan fungsi.
- Setelah menentukan f(x), pertimbangkan langkah antiturunan dari fungsi ini.
- Amati batas fungsi bawah dan atas, hitung dengan tepat dan terapkan batas tersebut pada integral tertentu
- Sekarang selesaikan limit dan selisih antara batas bawah dan batas atas.
- Temukan perbedaan antara penerapan dan jawaban integral.

Pentingnya integrasi
Ada berbagai pentingnya integrasi dan arti penting integrasi adalah:
- Luas di Bawah Kurva:
Penerapan utama integrasi adalah mencari luas di bawah kurva. Dan mengetahui luas grafik berbagai bentuk trigonometri. - Antiturunan:
Integrasi digunakan untuk mencari antiturunan dari perbandingan aljabar dan trigonometri integral tak tentu dan integral tertentu suatu fungsi. - Menyelesaikan Persamaan Diferensial:
Hubungan variabel bebas dan variabel terikat ditentukan oleh integrasi. Hal ini penting untuk menyelesaikan persamaan diferensial, yang menggambarkan bagaimana suatu fungsi berubah terhadap variabel independen. - Probabilitas dan Statistik:
Integral digunakan untuk menghitung probabilitas dan estimasi, proyeksi, dan berbagai properti statistik. Kalkulator integral sangat penting dalam statistik dan probabilitas
Kesimpulan:
Integrasi adalah alat utama untuk probabilitas, statistik, dan proyeksi. Kalkulator Integral digunakan untuk mencari hubungan antara variabel terikat dan bebas. Hal ini penting untuk mengetahui sifat hubungan antara variabel terikat dan bebas. Integrasi sangat penting dalam bidang teknik dan kalkulus.
Catatan Visualisai Integral dan Siginifikansi Pendidikannya di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.
Ayo Share (Berbagi) Satu Hal Baik.
Di waktu senggang saya melakukan kalkulus diferensial dan integral.

com.png)