
The good student, Calon Guru belajar matematika dasar SMA dari Cara Menentukan Fungsi Naik, Fungsi Turun dan Titik Stasioner Pada Fungsi Aljabar dan pada catatan ini kita berikan 30+ soal latihan yang dilengkapi dengan pembahasan.
Pada catatan sebelumnya kita sudah dapatkan hubungan turunan fungsi ajabar dengan gradien garis singgung kurva. Catatan berikut ini akan menggambarkan bagaimana hubungan turunan fungsi terhadap nilai fungsi yang naik atau turun.
FUNGSI NAIK DAN FUNGSI TURUN
Sebuah fungsi $f(x)$ naik atau turun dapat kita perhatikan dari nilai fungsi $f(x)$ untuk setiap nilai $x$ atau dengan memperhatikan grafik dari fungsi $f(x)$. Misal, coba kita perhatikan grafik dari fungsi $f(x)$ di bawah ini.

Dari gambar di atas kita perhatikan grafik fungsi $f(x)$ jika $x \lt A$ grafik naik, sedangkan untuk $A \lt x \lt B$ grafik fungsi $f(x)$ turun, dan untuk $x \gt B$ grafik fungsi $f(x)$ naik.
Jika untuk menentukan naik atau turunnya sebuah fungsi $f(x)$ kita ketahui dengan menganalisa gambar maka diperlukan banyak waktu, karena untuk menggambar grafik fungsi $f(x)$ berpangkat $3,4,5$ atau grafik fungsi $f(x)$ bentuk pecahan itu tingkat kesulitannya tinggi.
Untuk mengetahui naik atau turunnya sebuah fungsi $f(x)$ dapat kita gunakan bantuan turunan fungsi $f(x)$.
- Jika $f'(x) \gt 0$ maka fungsi $y=f(x)$ naik atau sebaliknya jika $y=f(x)$ naik maka $f'(x) \gt 0$
- Jika $f'(x) \lt 0$ maka fungsi $y=f(x)$ turun atau sebaliknya jika $y=f(x)$ turun maka $f'(x) \lt 0$
TITIK STASIONER
Titik stasioner terjadi saat $f'(x) = 0$ dengan kata lain pada suatu titik dimana fungsi tidak naik dan tidak turun maka titik itu disebut titik stasioner.
Titik stasioner ada dua, yaitu titik balik atau titik belok. Titik balik adalah titik dimana fungsi sebelum dan sesudah titik tersebut fungsi mengalami perubahan, dari fungsi naik menjadi fungsi turun atau dari fungsi turun menjadi fungsi naik.
Sedangkan titik belok adalah titik dimana sebelum dan sesudah titik tersebut fungsi tidak mengalami perubahan dari naik menjadi turun atau dari turun menjadi naik. Atau sebelum dan sesudah titik tersebut fungsi dari fungsi naik tetap fungsi naik atau dari fungsi turun tetap fungsi turun.
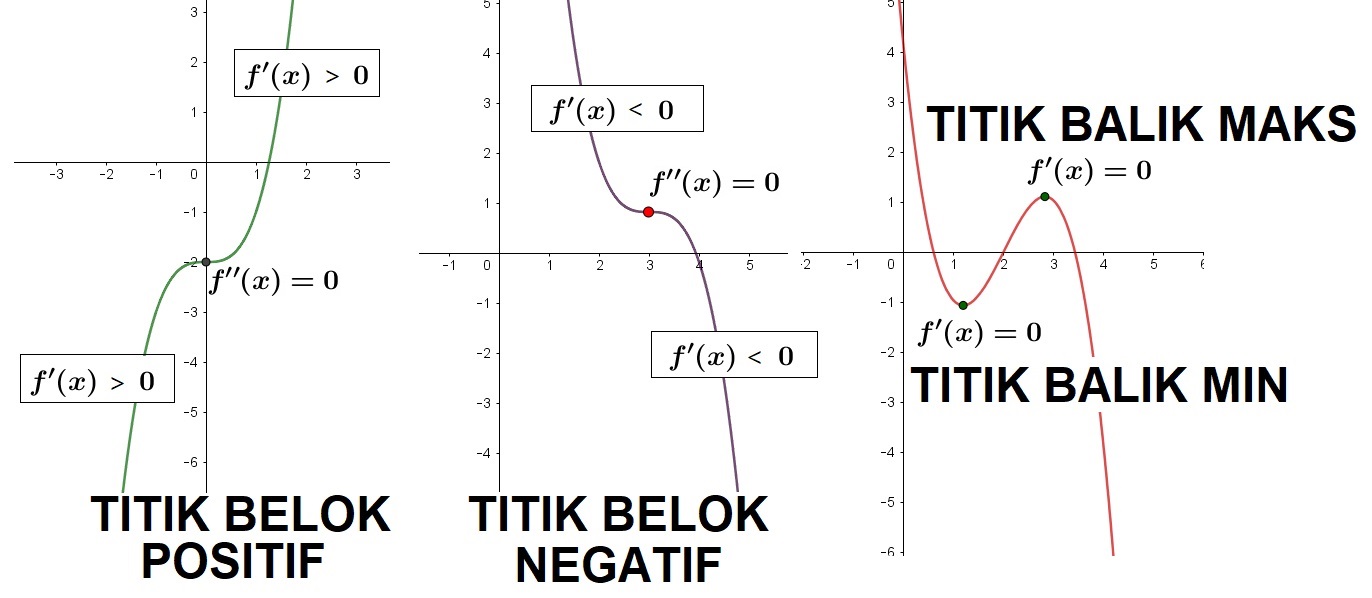
FUNGSI CEKUNG KE ATAS dan CEKUNG KE BAWAH
- Fungsi $f(x)$ dikatakan cekung ke atas dalam interval $A$ jika $f''(x) \gt 0$, untuk setiap $x \in A$.
- Fungsi $f(x)$ dikatakan cekung ke bawah dalam interval $A$ jika $f''(x) \lt 0$, untuk setiap $x \in A$.
- Saat $f''(x) = 0$ untuk $x=a$ maka titik belok adalah $\left(a, f(a) \right)$ dengan syarat:
- untuk $x \lt a$ fungsi cekung ke atas dan untuk $x \gt a$ fungsi cekung ke bawah, atau
- untuk $x \lt a$ fungsi cekung ke bawah dan untuk $x \gt a$ fungsi cekung ke atas.
SOAL LATIHAN dan PEMBAHASAN FUNGSI NAIK, FUNGSI TURUN, dan TITIK STASIONER
Untuk menambah pemahaman kita terkait Fungsi Naik, Fungsi Turun dan Titik Stasioner Pada Fungsi Aljabar mari kta coba berlatih dari beberapa soal latihan berikut. Soal latihan kita pilih dari soal latihan pada Modul Matematika SMA Fungsi Naik, Fungsi Turun dan Titik Stasioner Pada Fungsi Aljabar atau soal-soal yang ditanyakan pada media sosial.
Silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan Periksa Jawaban dan jika hasilnya belum memuaskan, pilih ⟳ Ulangi Tes untuk tes ulang. Ayo Tunjukkan Kemampuan Terbaikmu!
| Nama Peserta : | |
| Tanggal Tes : | |
| Jumlah Soal : | 32 soal |
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.
1. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)=3x^{2}-6x+5$ naik dalam interval...
Alternatif Pembahasan:
Syarat suatu fungsi $f(x)$ naik adalah saat $f'(x) \gt 0$
$ \begin{align} f(x) &= 3x^{2}-6x+5\\ f'(x) &= 6x-6 \\ \hline f'(x) & \gt 0 \\ 6x-6 & \gt 0 \\ 6x & \gt 6 \\ \dfrac{6x}{6} & \gt \dfrac{6}{6} \\ x & \gt 1 \end{align} $
Kesimpulan: fungsi $f(x)=3x^{2}-6x+5$ akan naik pada interval $x \gt 1$
$\therefore$ Pilihan yang sesuai adalah $(B)\ x \gt 1$
2. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)=-4x^{2}+24x-10$ turun dalam interval...
Alternatif Pembahasan:
Syarat suatu fungsi $f(x)$ turun adalah saat $f'(x) \lt 0$
$ \begin{align} f(x) &= -4x^{2}+24x-10 \\ f'(x) &= -8x+24 \\ \hline f'(x) & \lt 0 \\ -8x+24 & \lt 0 \\ -8x & \lt -24 \\ \dfrac{-8x}{-8} & \gt \dfrac{-24}{-8} \\ x & \gt 3 \end{align} $
Kesimpulan: fungsi $f(x)=-4x^{2}+24x-10$ akan turun pada interval $x \gt 3$
$\therefore$ Pilihan yang sesuai adalah $(E)\ x \gt 3$
3. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)=x^{3} – 9x^{2} + 24x – 12$ naik dalam interval
Alternatif Pembahasan:
Syarat suatu fungsi $f(x)$ naik adalah saat $f'(x) \gt 0$
$ \begin{align} f(x) &= x^{3} – 9x^{2} + 24x – 12 \\ f'(x) &= 3x^{2}-18x+24 \\ \hline f'(x) & \gt 0 \\ 3x^{2}-18x+24 & \gt 0 \\ 3 \left( x-2 \right)\left( x-4 \right) & \gt 0 \\ \hline \text{pembuat nol:}\ & x =2\ \text{atau}\ x =4 \\ \hline x \lt 2\ \text{atau}\ x \gt 4 & \end{align} $
Kesimpulan: fungsi $f(x)=x^{3} – 9x^{2} + 24x – 12$ akan naik pada interval $x \lt 2\ \text{atau}\ x \gt 4$
*Jika masih kesulitan menyelesaikan pertidaksamaan kuadrat dengan cepat silahkan disimak caranya: Cara Kreatif Menentukan HP Pertidaksamaan Kuadrat
$\therefore$ Pilihan yang sesuai adalah $(A)\ x \lt 2\ \text{atau}\ x \gt 4$
4. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)=-x^{3} -3x^{2} + 9x – 5$ naik dalam interval
Alternatif Pembahasan:
Syarat suatu fungsi $f(x)$ naik adalah saat $f'(x) \gt 0$
$ \begin{align} f(x) &= -x^{3} -3x^{2} + 9x – 5 \\ f'(x) &= -3x^{2} -6x+9 \\ \hline f'(x) & \gt 0 \\ -3x^{2} -6x+9 & \gt 0 \\ x^{2} +2x-3 & \lt 0 \\ \left( x+3 \right)\left( x-1 \right) & \lt 0 \\ \hline \text{pembuat nol:}\ & x =-3\ \text{atau}\ x =1 \\ \hline -3 \lt x \lt 1 & \end{align} $
Kesimpulan: fungsi $f(x)=-x^{3} -3x^{2} + 9x – 5$ akan naik pada interval $-3 \lt x \lt 1 $
*Jika masih kesulitan menyelesaikan pertidaksamaan kuadrat dengan cepat silahkan disimak caranya: Cara Kreatif Menentukan HP Pertidaksamaan Kuadrat
$\therefore$ Pilihan yang sesuai adalah $(E)\ -3 \lt x \lt 1 $
5. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)=x^{3} +2x^{2} + 2x – 5$ grafiknya...
Alternatif Pembahasan:
Untuk mengetahui kedudukan grafik suatu fungsi $f(x)$, dapat kita periksa dari turunan pertama fungsi tersebut $f'(x)$
$ \begin{align} f(x) &= x^{3} +2x^{2} + 2x – 5 \\ f'(x) &= 3x^{2}+4x+2 \end{align} $
Turunan pertama $f'(x) = 3x^{2}+4x+2$ selalu bernilai positif, dapat kita periksa dengan menghitung nilai diskriminan $D=b^{2}-4ac=-8$ dan $a=3$ (definit positif).
Karena $f'(x)$ selalu bernilai positif sehingga grafik fungsi $f(x)$ selalu naik.
*Untuk memeriksa fungsi kuadrat $f(x)= ax^{2}+bx+c$ apakah selalu bernilai positif atau negatif, dapat diperiksa dari nilai $D=b^{2}-4ac$ dan $a$.
- Jika $D \lt 0$ dan $a \gt 0$ maka fungsi selalu bernilai positif, disebut definit positif.
- Jika $D \lt 0$ dan $a \lt 0$ maka fungsi selalu bernilai negatif, disebut definit negatif.
$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{Selalu naik} $
6. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)=-x^{3} + x^{2} -4x +3$ grafiknya...
Alternatif Pembahasan:
Untuk mengetahui kedudukan grafik suatu fungsi $f(x)$, dapat kita periksa dari turunan pertama fungsi tersebut $f'(x)$
$ \begin{align} f(x) &= -x^{3} + x^{2} -4x +3 \\ f'(x) &= -3x^{2}+2x-4 \end{align} $
Turunan pertama $f'(x) = -3x^{2}+2x-4$ selalu bernilai negatif, dapat kita periksa dengan menghitung nilai diskriminan $D=b^{2}-4ac=-44$ dan $a=-3$ (definit negatif).
Karena $f'(x)$ selalu bernilai negatif sehingga grafik fungsi $f(x)$ selalu turun.
*Untuk memeriksa fungsi kuadrat $f(x)= ax^{2}+bx+c$ apakah selalu bernilai positif atau negatif, dapat diperiksa dari nilai $D=b^{2}-4ac$ dan $a$.
- Jika $D \lt 0$ dan $a \gt 0$ maka fungsi selalu bernilai positif, disebut definit positif.
- Jika $D \lt 0$ dan $a \lt 0$ maka fungsi selalu bernilai negatif, disebut definit negatif.
$\therefore$ Pilihan yang sesuai adalah $(E)\ \text{Selalu turun}$
7. Soal Latihan Fungsi Naik dan Fungsi Turun
Titik stasioner dari fungsi $f(x)= x^{2} + 4x -3$ adalah...
Alternatif Pembahasan:
Untuk mengetahui jenis titik stasioner dari fungsi $f(x)= x^{2} + 4x -3$ yang merupakan fungsi kuadrat dapat juga kita tentukan dengan aturan pada fungsi kuadrat.
Untuk memantapkan kita menggunakan konsep turunan fungsi, titik stasioner dari fungsi $f(x)= x^{2} + 4x -3$ kita tentukan dengan menggunakan konsep turunan fungsi.
$ \begin{align} f(x) &= x^{2} + 4x -3 \\ f'(x) &= 2x+4 \\ \hline f'(x) &= 0 \\ 2x+4 &= 0 \\ 2x &= -4 \\ x &= -2 \\ y &= f(x) \\ y &= f(-2) \\ &= (-2)^{2} + 4(-2) -3 \\ &= 4 -8 -3 = -7 \end{align} $
Titik stasioner fungsi $f(x)= x^{2} + 4x -3$ adalah $\left( -2,-7 \right)$.
Titik stasioner maksimum atau minimum suatu fungsi dapat kita periksa dari saat kapan fungsi naik atau turun.
Fungsi $f(x)= x^{2} + 4x -3$ turun saat $x \lt -2$ dan naik saat $x \gt -2$ sehingga saat $x=-2$ adalah titik balik minimum karena setelah $x=-2$ atau $x \gt -2$ fungsi naik.
Alternatif lain dapat kita gunakan dengan uji turunan kedua seperti berikut ini:
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \gt 0$ maka $x=a$ adalah pembuat $f(x)$ minimum atau nilai minimum $f(x)$ adalah $f(a)$.
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \lt 0$ maka $x=a$ adalah pembuat $f(x)$ maskimum atau nilai maksimum $f(x)$ adalah $f(a)$.
$ \begin{align} f(x) &= x^{2} + 4x -3 \\ f'(x) &= 2x+4 \\ f''(x) &= 2 \end{align} $
Untuk $x=-2$ kita peroleh $f''(-2) = 2 \gt 0$ sehingga $x=-2$ adalah pembuat $f(x)$ minimum dan nilai minimumnya adalah $f(-2)=-7$.
$\therefore$ Pilihan yang sesuai adalah $(A)\ \text{Titik minimum}\ \left( -2,-7 \right)$
8. Soal Latihan Fungsi Naik dan Fungsi Turun
Titik stasioner dari fungsi $f(x)= -x^{2} -2x +5$ adalah...
Alternatif Pembahasan:
Untuk mengetahui jenis titik stasioner dari fungsi $f(x)= -x^{2} -2x +5$ yang merupakan fungsi kuadrat dapat juga kita tentukan dengan aturan pada fungsi kuadrat.
Untuk memantapkan kita menggunakan konsep turunan fungsi, titik stasioner dari fungsi $f(x)= -x^{2} -2x +5$ kita tentukan dengan menggunakan konsep turunan fungsi.
$ \begin{align} f(x) &= -x^{2} -2x +5 \\ f'(x) &= -2x-2 \\ \hline f'(x) &= 0 \\ -2x-2 &= 0 \\ -2x &= 2 \\ x &= -1 \\ y &= f(x) \\ y &= f(-1) \\ &= -(-1)^{2} -2(-1) +5 \\ &= -1+2+5 = 6 \end{align} $
Titik stasioner fungsi $f(x)= -x^{2} -2x +5$ adalah $\left( -1,6 \right)$.
Titik stasioner maksimum atau minimum suatu fungsi dapat kita periksa dari saat kapan fungsi naik atau turun.
Fungsi $f(x)= -x^{2} -2x +5$ turun saat $x \gt -1$ dan naik saat $x \lt -1$ sehingga saat $x=-1$ adalah titik balik maksimum karena setelah $x=-1$ atau $x \gt -1$ fungsi turun.
Alternatif lain dapat kita gunakan dengan uji turunan kedua seperti berikut ini:
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \gt 0$ maka $x=a$ adalah pembuat $f(x)$ minimum atau nilai minimum $f(x)$ adalah $f(a)$.
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \lt 0$ maka $x=a$ adalah pembuat $f(x)$ maskimum atau nilai maksimum $f(x)$ adalah $f(a)$.
$ \begin{align} f(x) &= -x^{2} -2x +5 \\ f'(x) &= -2x-2 \\ f''(x) &= -2 \end{align} $
Untuk $x=-1$ kita peroleh $f''(-1) = -2 \lt 0$ sehingga $x=-1$ adalah pembuat $f(x)$ maksimum dan nilai maksimumnya adalah $f(-1)=6$.
$\therefore$ Pilihan yang sesuai adalah $(E)\ \text{Titik maksimum}\ \left( -1, 6 \right)$
9. Soal Latihan Fungsi Naik dan Fungsi Turun
Titik stasioner dari fungsi $f(x)= x^{3} – 3x^{2} – 24x$ adalah...
Alternatif Pembahasan:
Untuk mengetahui jenis titik stasioner dari fungsi $f(x)= x^{3} – 3x^{2} – 24x$ dapat kita gunakan dengan uji turunan kedua seperti berikut ini:
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \gt 0$ maka $x=a$ adalah pembuat $f(x)$ minimum atau nilai minimum $f(x)$ adalah $f(a)$.
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \lt 0$ maka $x=a$ adalah pembuat $f(x)$ maskimum atau nilai maksimum $f(x)$ adalah $f(a)$.
$ \begin{align} f(x) &= x^{3} – 3x^{2} – 24x \\ f'(x) &= 3x^{2}-6x-24 \\ \hline f'(x) &= 0 \\ 3x^{2}-6x-24 &= 0 \\ x^{2}-2x-8 &= 0 \\ \left( x-4 \right) \left( x+2 \right) &= 0 \\ x=4\ \text{atau}\ x=-2 & \\ y &= f(x) \\ y &= f(4) \\ &= (4)^{3} – 3(4)^{2} – 24(4) \\ &= 64-48-96 = -80 \\ \hline y &= f(-2) \\ &= (-2)^{3} – 3(-2)^{2} – 24(-2) \\ &= -8-12+48 = 28 \\ \end{align} $
Titik stasioner fungsi $f(x)= x^{3} – 3x^{2} – 24x$ adalah $\left( 4,-80 \right)$ dan $\left( -2,28 \right)$.
$ \begin{align} f(x) &= x^{3} – 3x^{2} – 24x \\ f'(x) &= 3x^{2}-6x-24 \\ f''(x) &= 6x-6 \end{align} $
Untuk $x=-2$ kita peroleh $f''(-2) = 6(-2)-6=-18 \lt 0$ sehingga $x=-2$ adalah pembuat $f(x)$ maksimum dan nilai maksimumnya adalah $f(-2)=28$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{Titik maksimum}\ \left( -2,28 \right)$
10. Soal Latihan Fungsi Naik dan Fungsi Turun
Titik stasioner dari fungsi $f(x)= x^{3} + 6x^{2} – 7$ adalah...
Alternatif Pembahasan:
Untuk mengetahui jenis titik stasioner dari fungsi $f(x)= x^{3} + 6x^{2} – 7$ dapat kita gunakan dengan uji turunan kedua seperti berikut ini:
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \gt 0$ maka $x=a$ adalah pembuat $f(x)$ minimum atau nilai minimum $f(x)$ adalah $f(a)$.
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \lt 0$ maka $x=a$ adalah pembuat $f(x)$ maskimum atau nilai maksimum $f(x)$ adalah $f(a)$.
$ \begin{align} f(x) &= x^{3} + 6x^{2} – 7 \\ f'(x) &= 3x^{2}-12x \\ \hline f'(x) &= 0 \\ 3x^{2}-12x &= 0 \\ x^{2}-4x &= 0 \\ \left( x \right) \left( x-4 \right) &= 0 \\ x=0\ \text{atau}\ x=4 & \\ y &= f(x) \\ y &= f(0) \\ &= (0)^{3} + 6(0)^{2} – 7 \\ &= 0+0-7 = -7 \\ \hline y &= f(4) \\ &= (-4)^{3} + 6(4)^{2} – 7 \\ &= -64+96-7 = 25 \\ \end{align} $
Titik stasioner fungsi $f(x)= x^{3} + 6x^{2} – 7$ adalah $\left( 0,-7 \right)$ dan $\left( -4,25 \right)$.
$ \begin{align} f(x) &= x^{3} + 6x^{2} – 7 \\ f'(x) &= 3x^{2}+12x \\ f''(x) &= 6x+12 \end{align} $
Untuk $x=-4$ kita peroleh $f''(-4) = 6(-4)+12=-12 \lt 0$ sehingga $x=-4$ adalah pembuat $f(x)$ maksimum dan nilai maksimumnya adalah $f(-4)=25$.
$\therefore$ Pilihan yang sesuai adalah $(E)\ \text{Titik maksimum}\ \left( -4, 25 \right)$
11. Soal Latihan Fungsi Naik dan Fungsi Turun
Diketahui fungsi $f(x)= 2x^{3} + 3x^{2} – 12x+10$. Nilai stasioner fungsi tersebut adalah...
Alternatif Pembahasan:
Untuk mengetahui jenis titik stasioner dari fungsi $f(x)= 2x^{3} + 3x^{2} – 12x+10$ dapat kita gunakan dengan uji turunan kedua seperti berikut ini:
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \gt 0$ maka $x=a$ adalah pembuat $f(x)$ minimum atau nilai minimum $f(x)$ adalah $f(a)$.
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \lt 0$ maka $x=a$ adalah pembuat $f(x)$ maskimum atau nilai maksimum $f(x)$ adalah $f(a)$.
$ \begin{align} f(x) &= 2x^{3} + 3x^{2} – 12x+10 \\ f'(x) &= 6x^{2}+6x-12 \\ \hline f'(x) &= 0 \\ 6x^{2}+6x-12 &= 0 \\ x^{2}+ x- 2 &= 0 \\ \left( x+2 \right) \left( x-1 \right) &= 0 \\ x=-2\ \text{atau}\ x=1 & \\ y &= f(x) \\ y &= f(-2) \\ &= 2(-2)^{3} + 3(-2)^{2} – 12(-2)+10 \\ &= -16 +12 + 24+10 = 30 \\ \hline y &= f(1) \\ &= 2(1)^{3} + 3(1)^{2} – 12(1)+10 \\ &= 2 + 3 -12 +10 = 3 \\ \end{align} $
Titik stasioner fungsi $f(x)= 2x^{3} + 3x^{2} – 12x+10$ adalah $\left( 1,3 \right)$ dan $\left( -2,30 \right)$.
$ \begin{align} f(x) &= 2x^{3} + 3x^{2} – 12x+10 \\ f'(x) &= 6x^{2}+6x-12 \\ f''(x) &= 12x + 6 \end{align} $
Untuk $x=1$ kita peroleh $f''(1) = 12(1)+6=18 \gt 0$ sehingga $x=1$ adalah pembuat $f(x)$ minimum dan nilai minimumnya adalah $f(1)=3$.
Sedangkan untuk $x=-2$ kita peroleh $f''(-2) = 12(-2)+6=-18 \lt 0$ sehingga $x=-2$ adalah pembuat $f(x)$ maksimum dan nilai maksimumnya adalah $f(-2)=30$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{Nilai minimum}\ 3$
12. Soal Latihan Fungsi Naik dan Fungsi Turun
Nilai stasioner fungsi $f(x)= x^{3} - 3x^{2} +2$ adalah...
Alternatif Pembahasan:
Untuk mengetahui jenis titik stasioner dari fungsi $f(x)= x^{3} - 3x^{2} +2$ dapat kita gunakan dengan uji turunan kedua seperti berikut ini:
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \gt 0$ maka $x=a$ adalah pembuat $f(x)$ minimum atau nilai minimum $f(x)$ adalah $f(a)$.
- Jika $x=a$ pada $f'(a)=0$ sehingga $f''(a) \lt 0$ maka $x=a$ adalah pembuat $f(x)$ maskimum atau nilai maksimum $f(x)$ adalah $f(a)$.
$ \begin{align} f(x) &= x^{3} - 3x^{2} +2 \\ f'(x) &= 3x^{2}-6x \\ \hline f'(x) &= 0 \\ 3x^{2}-6x &= 0 \\ \left( 3x \right) \left( x-2 \right) &= 0 \\ x=0\ \text{atau}\ x=2 & \\ y &= f(x) \\ y &= f(0) \\ &= (0)^{3} - 3(0)^{2} +2 \\ &= 0 - 0 + 2 = 2 \\ \hline y &= f(2) \\ &= (2)^{3} - 3(2)^{2} +2 \\ &= 8 - 12 + 2 = -2 \\ \end{align} $
Titik stasioner fungsi $f(x)= x^{3} - 3x^{2} +2$ adalah $\left( 0,2 \right)$ dan $\left( 2,-2 \right)$.
$ \begin{align} f(x) &= x^{3} - 3x^{2} +2 \\ f'(x) &= 3x^{2}-6x \\ f''(x) &= 6x - 6 \end{align} $
Untuk $x=0$ kita peroleh $f''(0) = 6(0) - 6 =-6 \lt 0$ sehingga $x=0$ adalah pembuat $f(x)$ maksimum dan nilai maksimumnya adalah $f(0)=2$.
Sedangkan untuk $x=2$ kita peroleh $f''(2) = 6(2)+6=18 \gt 0$ sehingga $x=2$ adalah pembuat $f(x)$ minimum dan nilai minimumnya adalah $f(2)=-2$.
$\therefore$ Pilihan yang sesuai adalah $(A)\ \text{Nilai maksimum}\ 2$
13. Soal Latihan Fungsi Naik dan Fungsi Turun
Nilai maksimum dari $f(x)= x^{2} -6x + 5$ dalam interval $0 \leq x \leq 5$ adalah...
Alternatif Pembahasan:
Untuk menghitung nilai maksimum dari $f(x)= x^{2} -6x + 5$ dalam interval $0 \leq x \leq 5$ dapat kita peroleh dengan menguji beberapa nilai $x$ ke fungsi $f(x)= x^{2} -6x + 5$.
$ \begin{align} f(x) &= x^{2} -6x + 5 \\ \hline f(0) &= (0)^{2} -6(0) + 5 \\ &= 0 -0+5=5 \\ \hline f(1) &= (1)^{2} -6(1) + 5 \\ &= 1 -6+5=0 \\ \hline f(2) &= (2)^{2} -6(2) + 5 \\ &= 4 -12+5=-3 \\ \hline f(3) &= (3)^{2} -6(3) + 5 \\ &= 9 -18+5=-4 \\ \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(A)\ 5$
14. Soal Latihan Fungsi Naik dan Fungsi Turun
Nilai minimum dari $f(x)= 2x^{3} -9x^{2}+12x$ dalam interval $0 \leq x \leq 3$ adalah...
Alternatif Pembahasan:
Untuk menghitung nilai minimum dari $f(x)= 2x^{3} -9x^{2}+12x$ dalam interval $0 \leq x \leq 3$ dapat kita peroleh dengan menguji beberapa nilai $x$ ke fungsi $f(x)= 2x^{3} -9x^{2}+12x$.
$ \begin{align} f(x) &= 2x^{3} -9x^{2}+12x \\ \hline f(0) &= 2(0)^{3} -9(0)^{2}+12(0) \\ &= 0 -0+0=0 \\ \hline f(1) &= 2(1)^{3} -9(1)^{2}+12(1) \\ &= 2 -9+12=5 \\ \hline f(2) &= 2(2)^{3} -9(2)^{2}+12(2) \\ &= 16 -36+24=4 \\ \hline f(3) &= 2(3)^{3} -9(3)^{2}+12(3) \\ &= 54 -81+36=9 \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(A)\ 0$
15. Soal Latihan Fungsi Naik dan Fungsi Turun
Nilai maksimum dari $f(x)= x^{3} -12x^{2}+6$ dalam interval $1 \leq x \leq 3$ adalah...
Alternatif Pembahasan:
Untuk menghitung nilai minimum dari $f(x)= x^{3} -12x^{2}+6$ dalam interval $1 \leq x \leq 3$ dapat kita peroleh dengan menguji beberapa nilai $x$ ke fungsi $f(x)= x^{3} -12x^{2}+6$.
$ \begin{align} f(x) &= x^{3} -12x^{2}+6 \\ \hline f(1) &= (1)^{3} -12(1)^{2}+6 \\ &= 1 -12+6=-5 \\ \hline f(2) &= (2)^{3} -12(2)^{2}+6 \\ &= 8 -48+6=-34 \\ \hline f(3) &= (3)^{3} -12(3)^{2}+6 \\ &= 27 -108+6=-75 \\ \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(B)\ -5$
16. Soal Latihan Fungsi Naik dan Fungsi Turun
Diketahui fungsi $f(x)= \dfrac{x+1}{x^{2}+x+1}$. Salah satu titik stasionernya adalah...
Alternatif Pembahasan:
Untuk mengetahui titik stasioner dari fungsi $f(x)= \dfrac{x+1}{x^{2}+x+1}$ dapat kita gunakan dengan turunan pertama seperti berikut ini:
$ \begin{align} f(x) &= \dfrac{x+1}{x^{2}+x+1} \\ f'(x) &= \dfrac{\left(1 \right)\left( x^{2}+x+1 \right)-\left( x+1\right)\left(2x+1 \right)}{\left(x^{2}+x+1 \right)^{2}} \\ &= \dfrac{x^{2}+x+1 -\left( 2x^{2}+3x+1 \right)}{\left(x^{2}+x+1 \right)^{2}} \\ &= \dfrac{-x^{2}-2x}{\left(x^{2}+x+1 \right)^{2}} \end{align} $
$ \begin{align} f'(x) &= 0 \\ \dfrac{-x^{2}-2x}{\left(x^{2}+x+1 \right)^{2}} &= 0 \\ -x^{2}-2x &= 0 \\ x^{2}+2x &= 0 \\ \left( x \right) \left( x+2 \right) &= 0 \\ x=0\ \text{atau}\ x=-2 & \\ y &= f(x) \\ y &= f(0) \\ &= \dfrac{0+1}{(0)^{2}+(0)+1} \\ &= \dfrac{1}{1} = 1 \\ \hline y &= f(-2) \\ &= \dfrac{-2+1}{(-2)^{2}+(-2)+1} \\ &= \dfrac{-1}{3} \end{align} $
Titik stasioner fungsi $f(x)= \dfrac{x+1}{x^{2}+x+1}$ adalah $\left( 0,1 \right)$ dan $\left( -2,\dfrac{-1}{3} \right)$.
$\therefore$ Pilihan yang sesuai adalah $(B)\ \left( 0, 1 \right) $
17. Soal Latihan Fungsi Naik dan Fungsi Turun
Diketahui fungsi $y= x-\sqrt{2x-p}$. Jika nilai minimum dari fungsi tersebut adalah $2$, maka nilai $p=\cdots$
Alternatif Pembahasan:
Diketahui nilai minimum dari fungsi $y= x-\sqrt{2x-p}$ adalah $2$. Untuk mendapatkan nilai minimum tersebut dapat kita gunakan dengan turunan pertama seperti berikut ini:
$ \begin{align} y &= x-\sqrt{2x-p} \\ y' &= 1- \dfrac{1}{2\sqrt{2x-p}} \cdot \left( 2 \right) \\ &= 1- \dfrac{1}{\sqrt{2x-p}} \end{align} $
$ \begin{align} y' &= 0 \\ 1- \dfrac{1}{\sqrt{2x-p}} &= 0 \\ 1 &= \dfrac{1}{\sqrt{2x-p}} \\ \sqrt{2x-p} &= 1 \\ 2x-p &= 1 \\ 2x & =1+p \\ x & = \dfrac{1+p}{2} \end{align} $
Untuk $x = \dfrac{1+p}{2}$ diketahui nilai minimum $y= x-\sqrt{2x-p}$ adalah $2$ sehingga dapat kita peroleh:
$ \begin{align}
y &= 2 \\
\dfrac{1+p}{2}-\sqrt{2\left(\dfrac{1+p}{2} \right)-p} &= 2 \\
\dfrac{1+p}{2}-\sqrt{ 1+p -p} &= 2 \\
\dfrac{1+p}{2}-1 &= 2 \\
\dfrac{1+p}{2} &= 3 \\
1+p &= 6 \\
p & = 5
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(B)\ 5$
18. Soal Latihan Fungsi Naik dan Fungsi Turun
Jika fungsi $f(x)= x^{3}+px^{2}-9x$ mencapai nilai maksimum stasioner pada $x=-3$, maka nilai $p$ adalah...
Alternatif Pembahasan:
Diketahui nilai maksimum dari fungsi $f(x)= x^{3}+px^{2}-9x$ saat $x=-3$. Untuk mendapatkan nilai maksimum tersebut dapat kita gunakan dengan turunan pertama seperti berikut ini:
$ \begin{align} f(x) &= x^{3}+px^{2}-9x \\ f'(x) &= 3x^{2}+2px -9 \end{align} $
$ \begin{align} f'(x) &= 0 \\ 3x^{2}+2px -9 &= 0 \end{align} $
Diketahui nilai maksimum $y= x^{3}+px^{2}-9x$ saat $x=-3$ sehingga $x=-3$ adalah salah satu akar dari $3x^{2}+2px -9 = 0$.
$ \begin{align}
3x^{2}+2px -9 &= 0 \\
3(-3)^{2}+2p(-3) -9 &= 0 \\
27-6p -9 &= 0 \\
-6p &= -18 \\
p &= 3
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(C)\ 3$
19. Soal Latihan Fungsi Naik dan Fungsi Turun
Grafik fungsi $f(x)= x^{3}-6x^{2}+15x-9$ cekung ke atas dalam interval...
Alternatif Pembahasan:
Untuk mengetahui kecekungan grafik fungsi $f(x)= x^{3}-6x^{2}+15x-9$, dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
- Fungsi $f(x)$ dikatakan cekung ke atas dalam interval $A$ jika $f''(x) \gt 0$, untuk setiap $x \in A$.
- Fungsi $f(x)$ dikatakan cekung ke bawah dalam interval $A$ jika $f''(x) \lt 0$, untuk setiap $x \in A$.
$ \begin{align} f(x) &= x^{3}-6x^{2}+15x-9 \\ f'(x) &= 3x^{2}-12x+15 \\ f''(x) &= 6x -12 \end{align} $
Agar grafik $f(x)$ cekung ke atas maka batasan nilai $x$ adalah:
$ \begin{align} f''(x) & \gt 0 \\ 6x-12 & \gt 0 \\ 6x & \gt 12 \\ x & \gt 2 \\ \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(B)\ x \gt 2$
20. Soal Latihan Fungsi Naik dan Fungsi Turun
Grafik fungsi $f(x)= x^{4}-4x^{3}-18x^{2}+24x-9$ cekung ke bawah dalam interval...
Alternatif Pembahasan:
Untuk mengetahui kecekungan grafik fungsi $f(x)= x^{4}-4x^{3}-18x^{2}+24x-9$, dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
- Fungsi $f(x)$ dikatakan cekung ke atas dalam interval $A$ jika $f''(x) \gt 0$, untuk setiap $x \in A$.
- Fungsi $f(x)$ dikatakan cekung ke bawah dalam interval $A$ jika $f''(x) \lt 0$, untuk setiap $x \in A$.
$ \begin{align} f(x) &= x^{4}-4x^{3}-18x^{2}+24x-9 \\ f'(x) &= 4x^{3}-12x^{2}-36x +24 \\ f''(x) &= 12x^{2}-24x -36 \end{align} $
Agar grafik $f(x)$ cekung ke bawah maka batasan nilai $x$ adalah:
$ \begin{align} f''(x) & \lt 0 \\ 12x^{2}-24x -36 & \lt 0 \\ x^{2}-2x -3 & \lt 0 \\ \left( x-3 \right)\left(x+1 \right) & \lt 0 \\ \hline \text{pembuat nol:}\ & x =3\ \text{atau}\ x =-1 \\ \hline -1 \lt x \lt 3 & \end{align} $
Kesimpulan: fungsi $f(x)= x^{4}-4x^{3}-18x^{2}+24x-9$ cekung ke bawah dalam interval $-1 \lt x \lt 3$
Jika masih kesulitan menyelesaikan pertidaksamaan kuadrat dengan cepat silahkan disimak caranya: Cara Kreatif Menentukan HP Pertidaksamaan Kuadrat
$\therefore$ Pilihan yang sesuai adalah $(D)\ -1 \lt x \lt 3$
21. Soal Latihan Fungsi Naik dan Fungsi Turun
Grafik fungsi $f(x)= x^{4}-12x^{3}+54x^{2}-60x+25$ memenuhi...
Alternatif Pembahasan:
Untuk mengetahui kecekungan grafik fungsi $f(x)= x^{4}-12x^{3}+54x^{2}-60x+25$, dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
- Fungsi $f(x)$ dikatakan cekung ke atas dalam interval $A$ jika $f''(x) \gt 0$, untuk setiap $x \in A$.
- Fungsi $f(x)$ dikatakan cekung ke bawah dalam interval $A$ jika $f''(x) \lt 0$, untuk setiap $x \in A$.
$ \begin{align} f(x) &= x^{4}-12x^{3}+54x^{2}-60x+25 \\ f'(x) &= 4x^{3}-36x^{2}+108x -60 \\ f''(x) &= 12x^{2}-72x +108 \\ &= 12 \left(x^{2}-6x +9 \right) \\ &= 12 \left(x-3 \right)^{2} \end{align} $
Dari hasil di atas kita peroleh $f''(x) = 12 \left(x-3 \right)^{2}$ sehingga $f''(x) \gt 0$ atau $f''(x)$ selalu bernilai positif maka grafik $f(x)= x^{4}-12x^{3}+54x^{2}-60x+25$ Tidak pernah cekung ke bawah.
Untuk pilihan $(E)\ \text{Memiliki titik belok di}\ x=3$ salah, karena setelah dan sebelum $x=3$ kecekungan grafik tidak berubah. Kita ketahui bahwa titik belok adalah titik dimana ada perubahan kecekungan grafik.
$\therefore$ Pilihan yang sesuai adalah $(D)\ \text{Tidak pernah cekung ke bawah}$
22. Soal Latihan Fungsi Naik dan Fungsi Turun
Titik belok fungsi $f(x)= x^{3}+6x^{2}+9x+ 5$ adalah...
Alternatif Pembahasan:
Untuk titik belok $f(x)= x^{3}+6x^{2}+9x+ 5$ dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
$ \begin{align}
f(x) &= x^{3}+6x^{2}+9x+ 5 \\
f'(x) &= 3x^{2}+12x +9 \\
f''(x) &= 6x+12 \\
\hline
f''(x) &= 0 \\
6x+12 &= 0 \\
6x &= -12 \\
x &= -2 \\
\hline
f(x) &= x^{3}+6x^{2}+9x+ 5 \\
f(-2) &= (-2)^{3}+6(-2)^{2}+9(-2)+ 5 \\
&= -8+24-18+ 5 \\
&= 3
\end{align} $
Dari hasil di atas kita periksa $\left( -2,3 \right)$ apakah merupakan titik belok.
Untuk $x \lt -2$ misal $x=-3$ kita peroleh:
$ \begin{align}
f''(x) &= 6x+12 \\
f''(-3) &= 6(-3)+12 \\
f''(-3) &= -6 \lt 0 \\
\text{fungsi}\ f(x)\ & \text{cekung ke bawah}
\end{align} $
Untuk $x \gt -2$ misal $x=0$ kita peroleh:
$ \begin{align}
f''(x) &= 6x+12 \\
f''(0) &= 6(0)+12 \\
f''(0) &= 12 \gt 0 \\
\text{fungsi}\ f(x)\ & \text{cekung ke atas}
\end{align} $
Dari hasil di atas kita peroleh bahwa $\left( -2,3 \right)$ merupakan titik belok.
$\therefore$ Pilihan yang sesuai adalah $(B)\ \left( -2,3 \right)$
23. Soal Latihan Fungsi Naik dan Fungsi Turun
Titik belok fungsi $f(x)= x^{4}-6x^{2}+5x+4$ adalah...
Alternatif Pembahasan:
Untuk titik belok $f(x)= x^{4}-6x^{2}+5x+4$ dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
$ \begin{align}
f(x) &= x^{4}-6x^{2}+5x+4 \\
f'(x) &= 4x^{3}-12x+5 \\
f''(x) &= 12x^{2}-12 \\
\hline
f''(x) &= 0 \\
12x^{2}-12 &= 0 \\
x^{2}-1 &= 0 \\
\left(x-1 \right)\left(x+1 \right) &= 0 \\
x=1\ \text{atau}\ x=-1 & \\
\hline
f(x) &= x^{4}-6x^{2}+5x+4 \\
f(1) &= (1)^{4}-6(1)^{2}+5(1)+4 \\
&= 1-6+5+4=4 \\
\hline
f(x) &= x^{4}-6x^{2}+5x+4 \\
f(-1) &= (-1)^{4}-6(-1)^{2}+5(-1)+4 \\
&= 1-6-5+4=-6
\end{align} $
Dari hasil di atas kita periksa $\left( -1,-6 \right)$ atau $\left( 1,4 \right)$ apakah merupakan titik belok.
Untuk $x \lt -1$ misal $x=-2$ kita peroleh:
$ \begin{align}
f''(x) &= 12x^{2}-12 \\
f''(-2) &= 12(2)^{2}-12 \\
f''(-2) &= 36 \gt 0 \\
\text{fungsi}\ f(x)\ & \text{cekung ke atas}
\end{align} $
Untuk $x \gt -1$ misal $x=0$ kita peroleh:
$ \begin{align}
f''(x) &= 12x^{2}-12 \\
f''(0) &= 12(0)^{2}-12 \\
f''(0) &= -12 \lt 0 \\
\text{fungsi}\ f(x)\ & \text{cekung ke bawah}
\end{align} $
Dari hasil di atas kita peroleh bahwa $\left( -1,-6 \right)$ merupakan titik belok.
$\therefore$ Pilihan yang sesuai adalah $(A)\ \left( -1,-6 \right)$
24. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)= 3x^{5} – 10x^{4} + 10x^{3} – 60x – 40$ memiliki titik belok...
Alternatif Pembahasan:
Untuk titik belok $f(x)= 3x^{5} – 10x^{4} + 10x^{3} – 60x – 40$ dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
$ \begin{align}
f(x) &= 3x^{5} – 10x^{4} + 10x^{3} – 60x – 40 \\
f'(x) &= 15x^{4} – 40x^{3} + 30x^{2} – 60 \\
f''(x) &= 60x^{3}-120x^{2}+60x \\
\hline
f''(x) &= 0 \\
60x^{3}-120x^{2}+60x &= 0 \\
x^{3}-2x^{2}+x &= 0 \\
\left(x \right)\left( x^{2}-2x+1 \right) &= 0 \\
\left(x \right)\left(x-1 \right)\left(x-1 \right) &= 0 \\
x=0\ \text{atau}\ x=1 & \\
\hline
f(x) &= 3x^{5} – 10x^{4} + 10x^{3} – 60x – 40 \\
f(1) &= 3(1)^{5} – 10(1)^{4} + 10(1)^{3} – 60(1) – 40 \\
&= 3-10+10-60-40=-97 \\
\hline
f(x) &= 3x^{5} – 10x^{4} + 10x^{3} – 60x – 40 \\
f(0) &= 3(2)^{5} – 10(0)^{4} + 10(0)^{3} – 60(0) – 40 \\
&= 0-0+0-0-40=-40 \\
\end{align} $
Dari hasil di atas kita periksa $\left( 1,97 \right)$ atau $\left( 0,-40 \right)$ apakah merupakan titik belok.
Untuk $x \lt 0$ misal $x=-1$ kita peroleh:
$ \begin{align}
f''(x) &= 60x^{3}-120x^{2}+60x \\
f''(-1) &= 60(-1)^{3}-120(-1)^{2}+60(-1) \\
f''(-2) &= -240 \lt 0 \\
\text{fungsi}\ f(x)\ & \text{cekung ke bawah}
\end{align} $
Untuk $x \gt 0$ misal $x=0,5$ kita peroleh:
$ \begin{align}
f''(x) &= 60x^{3}-120x^{2}+60x \\
f''(0,5) &= 60(0,5)^{3}-120(0,5)^{2}+60(0,5) \\
f''(0,5) &= 7,5 \gt 0 \\
\text{fungsi}\ f(x)\ & \text{cekung ke atas}
\end{align} $
Dari hasil di atas kita peroleh bahwa $\left( 0,-40 \right)$ merupakan titik belok. Silahkan dibuktikan bahwa $\left( 1,97 \right)$ bukan merupakan titik belok.
$\therefore$ Pilihan yang sesuai adalah $(A)\ \left( 0,-40 \right)$
25. Soal Latihan Fungsi Naik dan Fungsi Turun
Jika titik belok dari fungsi $f(x)= x^{3} +bx^{2} + 9x – a$ adalah $\left(-2,7\right)$, maka nilai $a=\cdots$
Alternatif Pembahasan:
Untuk titik belok $\left(-2,7\right)$ pada fungsi $f(x)= x^{3} +bx^{2} + 9x – a$ dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
$ \begin{align} f(x) &= x^{3} +bx^{2} + 9x – a \\ f'(x) &= 3x^{2} +2bx + 9 \\ f''(x) &= 6x +2b \\ \hline f''(x) &= 0 \\ 6x +2b &= 0 \\ 6x &= -2b \\ x &= \dfrac{-2b}{6} \\ (-2) &= \dfrac{-2b}{6} \\ 6 &= b \\ \hline f(x) &= x^{3} +bx^{2} + 9x – a \\ f(-2) &= (-2)^{3} +b(-2)^{2} + 9(-2) – a \\ 7 &= -8 +(6)(4) -18 – a \\ -9 &= a \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(A)\ -9$
26. Soal Latihan Fungsi Naik dan Fungsi Turun
Grafik fungsi $f(x)=\left(4-x \right)^{3} – \left(4-x \right)^{2}$ akan naik dalam interval...
Alternatif Pembahasan:
Syarat suatu fungsi $f(x)$ naik adalah saat $f'(x) \gt 0$
$ \begin{align} f(x) &= \left(4-x \right)^{3} – \left(4-x \right)^{2} \\ f'(x) &= 3\left(4-x \right)^{2}\left( -1 \right) – 2\left(4-x \right) \left( -1 \right) \\ &= -3\left( x^{2}-8x+16 \right) + 2\left(4-x \right) \\ &= -3x^{2}+24x-48 + 8-2x \\ &= -3x^{2}+22x-40 \\ \hline f'(x) & \gt 0 \\ -3x^{2}+22x-40 & \gt 0 \\ 3x^{2}-22x+40 & \lt 0 \\ \left( 3x-10 \right)\left( x-4 \right) & \lt 0 \\ \hline \text{pembuat nol:}\ & x =\frac{3}{10}\ \text{atau}\ x =4 \\ \hline 3\frac{1}{3} \lt x \lt 4 & \end{align} $
Kesimpulan: fungsi $f(x)=\left(4-x \right)^{3} – \left(4-x \right)^{2}$ akan naik pada interval $3\frac{1}{3} \lt x \lt 4$
Jika masih kesulitan menyelesaikan pertidaksamaan kuadrat dengan cepat silahkan disimak caranya: Cara Kreatif Menentukan HP Pertidaksamaan Kuadrat
$\therefore$ Pilihan yang sesuai adalah $(C)\ 3\frac{1}{3} \lt x \lt 4$
27. Soal Latihan Fungsi Naik dan Fungsi Turun
Fungsi $f(x)=\left(x-8 \right) \left( x^{2}+2x+1 \right)$ turun dalam interval...
Alternatif Pembahasan:
Syarat suatu fungsi $f(x)$ turun adalah saat $f'(x) \lt 0$
$ \begin{align} f(x) &= \left(x-8 \right) \left( x^{2}+2x+1 \right) \\ f'(x) &= \left( 1 \right) \left( x^{2}+2x+1 \right)+\left( x-8 \right) \left( 2x +2 \right) \\ &= x^{2}+2x+1 + 2x^{2} +2x-16x-16 \\ &= 3x^{2}-12x -15 \\ \hline f'(x) & \lt 0 \\ 3x^{2}-12x -15 & \lt 0 \\ x^{2}-4x - 5 & \lt 0 \\ \left( x-5 \right)\left( x+1 \right) & \lt 0 \\ \hline \text{pembuat nol:}\ & x =5\ \text{atau}\ x =-1 \\ \hline -1 \lt x \lt 5 & \end{align} $
Kesimpulan: fungsi $f(x)=\left(x-8 \right) \left( x^{2}+2x+1 \right)$ akan turun pada interval $-1 \lt x \lt 5$
Jika masih kesulitan menyelesaikan pertidaksamaan kuadrat dengan cepat silahkan disimak caranya: Cara Kreatif Menentukan HP Pertidaksamaan Kuadrat
$\therefore$ Pilihan yang sesuai adalah $(B)\ -1 \lt x \lt 5$
28. Soal Latihan Fungsi Naik dan Fungsi Turun
Nilai maksimum dari $f(x)= 6x^{2}-x^{3}$ dalam interval $-1 \leq x \leq 5$ adalah...
Alternatif Pembahasan:
Untuk menghitung nilai minimum dari $f(x)= 6x^{2}-x^{3}$ dalam interval $-1 \leq x \leq 5$ dapat kita peroleh dengan menguji beberapa nilai $x$ ke fungsi $f(x)= 6x^{2}-x^{3}$.
$ \begin{align} f(x) &= 6x^{2}-x^{3} \\ \hline f(-1) &= 6(-1)^{2}-(-1)^{3} \\ &= 6+1 =7 \\ \hline f(0) &= 6(0)^{2}-(0)^{3} \\ &= 0+0 =0 \\ \hline f(1) &= 6(1)^{2}-(1)^{3} \\ &= 6-1 =5 \\ \hline f(2) &= 6(2)^{2}-(2)^{3} \\ &= 24-8 =16 \\ \hline f(3) &= 6(3)^{2}-(3)^{3} \\ &= 54-27 =27 \\ \hline f(4) &= 6(4)^{2}-(4)^{3} \\ &= 96-64 =32 \\ \hline f(5) &= 6(5)^{2}-(5)^{3} \\ &= 150-125 =25 \\ \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(D)\ 32$
29. Soal Latihan Fungsi Naik dan Fungsi Turun
Jika titik belok $y= x^{3} +ax^{2} + bx – 3$ adalah $\left(-1,-4 \right)$, maka nilai $b=\cdots$
Alternatif Pembahasan:
Untuk titik belok $\left(-1,-4 \right)$ pada fungsi $y= x^{3} +ax^{2} + bx – 3$ dapat kita periksa dari turunan kedua fungsi tersebut seperti berikut ini:
$ \begin{align} f(x) &= x^{3} +ax^{2} + bx – 3 \\ f'(x) &= 3x^{2} +2ax + b \\ f''(x) &= 6x +2a \\ \hline f''(x) &= 0 \\ 6x +2a &= 0 \\ 6x &= -2a \\ x &= \dfrac{-2a}{6} \\ (-1) &= \dfrac{-2a}{6} \\ 3 &= a \\ \hline f(x) &= x^{3} +ax^{2} + bx – 3 \\ f(-1) &= (-1)^{3} +a(-1)^{2} + b(-1) – 3 \\ -4 &= -1 +(3)(1) -b – 3 \\ 3 &= b \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(E)\ 3$
30. Soal Latihan Fungsi Naik dan Fungsi Turun
Jika nilai maksimum fungsi $y= x+\sqrt{p-2x}$ adalah $4$, maka $p=\cdots$
Alternatif Pembahasan:
Diketahui nilai maksimum dari fungsi $y= x+\sqrt{p-2x}$ adalah $4$. Untuk mendapatkan nilai minimum tersebut dapat kita gunakan dengan turunan pertama seperti berikut ini:
$ \begin{align} y &= x+\sqrt{p-2x} \\ y' &= 1+ \dfrac{1}{2\sqrt{p-2x}} \cdot \left( -2 \right) \\ &= 1 - \dfrac{1}{\sqrt{p-2x}} \end{align} $
$ \begin{align} y' &= 0 \\ 1 - \dfrac{1}{\sqrt{p-2x}} &= 0 \\ 1 &= \dfrac{1}{\sqrt{p-2x}} \\ \sqrt{p-2x} &= 1 \\ p-2x &= 1 \\ 2x & = p-1 \\ x & = \dfrac{p-1}{2} \end{align} $
Untuk $x = \dfrac{p-1}{2}$ diketahui nilai minimum $y= x+\sqrt{p-2x}$ adalah $4$ sehingga dapat kita peroleh:
$ \begin{align}
y &= 4 \\
\dfrac{p-1}{2}+\sqrt{p-2\left( \dfrac{p-1}{2} \right)} &= 4 \\
\dfrac{p-1}{2}+\sqrt{p- \left( p-1 \right)} &= 4 \\
\dfrac{p-1}{2}+\sqrt{1} &= 4 \\
\dfrac{p-1}{2} &= 3 \\
p-1 &= 6 \\
p & = 7
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(D)\ 7$
31. Soal Latihan Fungsi Naik dan Fungsi Turun
Batas nilai $p$ agar fungsi $f(x)=-\dfrac{1}{3}x^{3} +px^{2} + 2px + 5$ selalu turun untuk semua nilai $x$ bilangan real adalah...
Alternatif Pembahasan:
Untuk mengetahui fungsi $f(x)=-\dfrac{1}{3}x^{3} +px^{2} + 2px + 5$ selalu turun maka dapat kita periksa dari turunan pertama fungsi tersebut selalu kurang dari nol.
$ \begin{align} f(x) &= -\dfrac{1}{3}x^{3} +px^{2} + 2px + 5 \\ f'(x) &= -\dfrac{1}{3} \cdot (3) x^{3-1} +2 \cdot px^{2-1} + 2p \\ f'(x) &= -x^{2} +2px + 2p \end{align} $
Untuk mengetahui turunan pertama $f'(x) = -x^{2} +2px + 2p$ selalu kurang dari nol (definit negatif) ada dua syarat yang harus dipenuhi yaitu:
Syarat pertama $a \lt 0$, sudah dipenuhi karena $a=-1$
Syarat kedua yaitu Diskriminan harus kurang dari nol.
$ \begin{align}
D & \lt 0 \\
b^{2}-4ac & \lt 0 \\
\left( 2p \right)^{2}-4\left( -1 \right)\left( 2p \right) & \lt 0 \\
4p^{2}+8p & \lt 0 \\
\left( 4p \right)\left( p+2 \right) & \lt 0 \\
p=0\ \text{atau}\ p=-2 & \\
-2 \lt p \lt 0 &
\end{align} $
Kesimpulan: fungsi $f(x)=-\dfrac{1}{3}x^{3} +px^{2} + 2px + 5$ selalu turun dalam interval $-2 \lt p \lt 0$
Jika masih kesulitan menyelesaikan pertidaksamaan kuadrat dengan cepat silahkan disimak caranya: Cara Kreatif Menentukan HP Pertidaksamaan Kuadrat
$\therefore$ Pilihan yang sesuai adalah $(A)\ -2 \lt p \lt 0$
32. Soal Latihan Fungsi Naik dan Fungsi Turun
Diketahui kurva $y=\dfrac{1}{3}x^{3}+x^{2}-3x+7$
Tentukan:
$(a)$ Turunan Pertama,
$(b)$ Interval untuk fungsi naik dan fungsi turun,
$(c)$ Nilai balik maksimum dan nilai balik minimum,
$(d)$ Gambarkan sketsa grafik.
Alternatif Pembahasan:
$(a)$. Turunan Pertama,
$ \begin{align}
y &= \dfrac{1}{3}x^{3}+x^{2}-3x+7 \\
y' &= 3 \cdot \dfrac{1}{3} x^{3-1}+2x^{2-1}-3 \\
y' &= x^{2}+2x-3
\end{align} $
$(b)$. Interval untuk fungsi naik,
Syarat suatu fungsi $y$ naik saat $y' \gt 0$
$ \begin{align}
y' & \gt 0 \\
x^{2}+2x-3 & \gt 0 \\
\left( x+3 \right)\left( x-1 \right) & \gt 0 \\
\hline
\text{pembuat nol:}\ & x =-3\ \text{atau}\ x =1 \\
\hline
x \lt -3\ \text{atau}\ x \gt 1 &
\end{align} $
Kesimpulan: fungsi $y=\dfrac{1}{3}x^{3}+x^{2}-3x+7$ akan naik pada interval $x \lt -3\ \text{atau}\ x \gt 1$
Jika masih kesulitan menyelesaikan pertidaksamaan kuadrat dengan cepat silahkan disimak caranya: Cara Kreatif Menentukan HP Pertidaksamaan Kuadrat
$(b)$. Interval untuk fungsi turun,
Syarat suatu fungsi $y$ naik saat $y' \lt 0$
$ \begin{align}
y' & \lt 0 \\
x^{2}+2x-3 & \lt 0 \\
\left( x+3 \right)\left( x-1 \right) & \lt 0 \\
\hline
\text{pembuat nol:}\ & x =-3\ \text{atau}\ x =1 \\
\hline
-3\ \lt x \lt 1 &
\end{align} $
Kesimpulan: fungsi $y=\dfrac{1}{3}x^{3}+x^{2}-3x+7$ akan turun pada interval $-3\ \lt x \lt 1$
$(c)$. Nilai balik maksimum relatif dan nilai balik minimum relatif,
Untuk menentukan nilai maksimum/minimum relatif fungsi $y$ dapat kita uji nilai $x=-3$ dan $x=1$ ke fungsi $y$.
$ \begin{align}
y &= \dfrac{1}{3}x^{3}+x^{2}-3x+7 \\
y &= \dfrac{1}{3}(-3)^{3}+(-3)^{2}-3(-3)+7 \\
&= -9+9+9+7= 16 \\
\hline
y &= \dfrac{1}{3}(1)^{3}+(1)^{2}-3(1)+7 \\
&= \dfrac{1}{3}+1-3+7= 4\dfrac{2}{3}
\end{align} $
Nilai maksimum relatif adalah $16$ dan nilai minimum relatif adalah $4\dfrac{2}{3}$.
(d). Gambarkan sketsa grafik

Catatan Cara Menentukan Fungsi Naik, Fungsi Turun dan Titik Stasioner Pada Fungsi Aljabar di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW
Ayo Share (Berbagi) Satu Hal Baik.
Jangan jadikan sekolah hanya untuk mencari nilai, tetapi bagaimana sekolah itu menjadikanmu bernilai.

com.png)