35 Soal PAS-SAS IPAS Semester Ganjil Kelas VI SD/MI dan Kunci Jawaban (B)

Calon Guru belajar Penalaran Matematika Soal Simulasi Tes UTBK-SNBT Tahun 2023. Sumber soal Simulasi Tes UTBK-SNBT Tahun 2023 ini berasal dari https://simulasi-tes.bppp.kemdikbud.go.id bagian Penalaran Matematika.

Seperti yang sudah disampaikan pada catatan sebelumnya bahwa Komponen Ujian Tertulis Berbasis Komputer dalam Seleksi Nasional Penerimaan Mahasiswa Baru (UTBK-SNPMB) Tahun 2023 terdiri dari beberapa sub tes, total soal ada $155$ soal dengan waktu $195$ menit, dan penjabaran waktu yang dibutuhkan dalam setiap tes seperti berikut ini.

Jenis Tes	Soal	waktu
1. Penalaran Umum Penalaran Induktif $10$ soal $10$ menit Penalaran Deduktif $10$ soal $10$ menit Penalaran Kuantitatif $10$ soal $10$ menit	$30$	$30$ menit
2. Pengetahuan dan Pemahaman Umum	$20$	$15$ menit
3. Kemampuan Memahami Bacaan dan Menulis	$20$	$25$ menit
4. Pengetahuan Kuantitatif	$15$	$20$ menit
5. Literasi dalam Bahasa Indonesia	$30$	$45$ menit
6. Literasi dalam Bahasa Inggris	$20$	$30$ menit
7. Penalaran Matematika	$20$	$30$ menit
Jumlah	$155$	$195$ menit

---

SOAL PENALARAN MATEMATIKA UTBK-SNBT 2023

Soal latihan penalaran matematika berikut ini, silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan Periksa Jawaban dan jika hasilnya belum memuaskan, pilih ⟳ Ulangi Tes untuk tes ulang. Ayo Tunjukkan Kemampuan Terbaikmu!

TKA Matematika UTBK SNBT

Nama Peserta :
Tanggal Tes :	Kamis, 4 Desember 2025
Jumlah Soal :	10 soal

Petunjuk Pengerjaan Soal:
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.

1. Soal Penalaran Matematika SNBT 2023

Dalam suatu kelas terdapat $12$ murid laki-laki dan $16$ murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah $80$. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada $4$ murid, dengan nilai masing-masing $52$, $56$, $62$, dan $66$, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik $7$ poin.

Jika sebelum remedial, rata-rata nilai ulangan murid laki-laki di kelas tersebut adalah $78$, rata-rata nilai ulangan murid perempuan adalah...

$(A)\ 80,5$

$(B)\ 81$

$(C)\ 81,5$

$(D)\ 82$

$(E)\ 82,5$

Alternatif Pembahasan:

Dari informasi pada soal, diketahui rata-rata nilai ulangan murid $12$ laki-laki di kelas tersebut adalah $78$, dengan menggunakan aturan menghitung rata-rata data tunggal dapat kita peroleh:
$\begin{align} \bar{x}\ & = \dfrac{l_{l}+l_{2}+\cdots+l_{12}}{n_{l}} \\ 78\ & = \dfrac{l_{l}+l_{2}+\cdots+l_{12}}{12} \\ 78 \times 12\ & = l_{l}+l_{2}+\cdots+l_{12} \\ 936\ & = l_{l}+l_{2}+\cdots+l_{12} \end{align}$

Diketahui dalam kelas terdapat $12$ murid laki-laki dan $16$ murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah $80$.
Dengan menggunakan aturan menghitung rata-rata data tunggal dapat kita peroleh:
$\begin{align} \bar{x}\ & = \dfrac{l_{l}+l_{2}+\cdots+l_{12}+p_{l}+p_{2}+\cdots+p_{16}}{n_{l}+n_{p}} \\ 80\ & = \dfrac{l_{l}+l_{2}+\cdots+l_{12}+p_{l}+p_{2}+\cdots+p_{16}}{12+16} \\ 80 \times 28\ & = l_{l}+l_{2}+\cdots+l_{12}+p_{l}+p_{2}+\cdots+p_{16} \\ 2.240\ & = l_{l}+l_{2}+\cdots+l_{12}+p_{l}+p_{2}+\cdots+p_{16} \\ 2.240\ & = 936+p_{l}+p_{2}+\cdots+p_{16} \\ 2.240-936\ & = p_{l}+p_{2}+\cdots+p_{16} \\ 1.304\ & = p_{l}+p_{2}+\cdots+p_{16} \\ \hline \bar{x}_{p}\ & = \dfrac{p_{l}+p_{2}+\cdots+p_{16}}{n_{p}} \\ \bar{x}_{p}\ & = \dfrac{1.304}{16} = 81,5 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 81,5$

2. Soal Penalaran Matematika SNBT 2023

Dalam suatu kelas terdapat $12$ murid laki-laki dan $16$ murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah $80$. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada $4$ murid, dengan nilai masing-masing $52$, $56$, $62$, dan $66$, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik $7$ poin.

Diberikan pernyataan berikut.

1. Rata-rata nilai kelas tanpa memperhitungkan keempat murid yang mengikuti remedial adalah $83,5$.
2. Sebelum remedial, rata-rata nilai ulangan murid yang mengikuti remedial adalah $60$.
3. Setelah remedial, rata-rata nilai ulangan seluruh murid menjadi $81$.
4. Jangkauan data nilai murid yang mengikuti remedial adalah $15$.

Pernyataan di atas yang benar adalah...

$(A)\ 1,2,\ \text{dan}\ 3$

$(B)\ 1\ \text{dan}\ 3$

$(C)\ 2\ \text{dan}\ 4$

$(D)\ 4$

$(E)\ 1,2,3,\ \text{dan}\ 4$

Alternatif Pembahasan:

1. Rata-rata nilai kelas tanpa memperhitungkan keempat murid yang mengikuti remedial adalah $83,5$ (BENAR).
   Dari nilai rata-rata ulangan Matematika $28$ murid di kelas tersebut $80$ dapat kita peroleh:
   $\begin{align} \bar{x}\ & = \dfrac{m_{l}+ \cdots+m_{28}}{28} \\ 80\ & = \dfrac{m_{l}+m_{2}+ \cdots+m_{28}}{28} \\ 80 \times 28\ & = m_{l}+m_{2}+ \cdots+m_{28} \\ 2.240\ & = m_{l}+m_{2}+ \cdots+m_{28} \\ 2.240\ & = m_{l}+m_{2}+ \cdots+m_{24}+52+56+62+66 \\ 2.240\ & = m_{l}+m_{2}+ \cdots+m_{24}+236 \\ 2.240-236\ & = m_{l}+m_{2}+ \cdots+m_{24} \\ 2.004\ & = m_{l}+m_{2}+ \cdots+m_{24} \\ \hline \bar{x}_{24}\ & = \dfrac{m_{l}+m_{2}+ \cdots+m_{24}}{24} \\ \bar{x}_{24}\ & = \dfrac{2.004}{24}=83,5 \end{align}$
2. Sebelum remedial, rata-rata nilai ulangan murid yang mengikuti remedial adalah $60$ (SALAH).
   Dari nilai murid $52$, $56$, $62$, dan $66$ rata-ratanya adalah:
   $\begin{align} \bar{x}\ & = \dfrac{m_{l}+m_{2}+ \cdots+m_{4}}{4} \\ & = \dfrac{52+56+62+66}{4} \\ & = \dfrac{236}{4}=59 \end{align}$
3. Setelah remedial, rata-rata nilai ulangan seluruh murid menjadi $81$ (BENAR).
   Nilai murid yang mengikuti remedial naik $7$ poin, sehingga jumlah nilai seluruh siswa bertambah $4 \times 7=28$ menjadi $2.240+28=2.268$.
   $\begin{align} \bar{x}\ & = \dfrac{m_{l}+ m_{2}+\cdots+m_{28}}{28} \\ & = \dfrac{2.268}{28}=81 \end{align}$
4. Jangkauan data nilai murid yang mengikuti remedial adalah $15$ (SALAH).
   Dari nilai murid $52$, $56$, $62$, dan $66$ jangkauannya adalah:
   $\begin{align} R\ & = x_{max} - x_{min} \\ & = 66-52=14 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 1\ \text{dan}\ 3$

3. Soal Penalaran Matematika SNBT 2023

Dalam suatu kelas terdapat $12$ murid laki-laki dan $16$ murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah $80$. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada $4$ murid, dengan nilai masing-masing $52$, $56$, $62$, dan $66$, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik $7$ poin.

Akan dipilih pengurus inti kelas yang terdiri dari $5$ murid.
Diberikan pernyataan berikut.

1. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid perempuan adalah $4.368$.
2. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid laki-laki adalah $495$.
3. Banyaknya cara memilih sehingga terdapat tepat $2$ murid laki-laki sebagai pengurus inti adalah $36.960$.

Nilai kebenaran pernyataan di atas secara berurutan adalah...

$(A)\ \text{Benar-Benar-Benar}$

$(B)\ \text{Benar-Benar-Salah}$

$(C)\ \text{Benar-Salah-Benar}$

$(D)\ \text{Benar-Salah-Salah}$

$(E)\ \text{Salah-Salah-Salah}$

Alternatif Pembahasan:

1. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid perempuan adalah $4.368$. (BENAR)
   Akan dipilih $5$ murid perempuan dari $16$ murid, dengan menggunakan aturan menggunakan Kombinasi dalam menyelesaikan masalah dapat kita peroleh:

   $\begin{align} C \left( n,r \right) & = \dfrac{n!}{r!(n-r)!} \\ C \left( 16,5 \right) & = \dfrac{16!}{5!(16-5)!} \\ & = \dfrac{16 \cdot 15 \cdot 14 \cdot 13 \cdot 12 \cdot 11!}{5!(11)!} \\ & = \dfrac{16 \cdot 15 \cdot 14 \cdot 13 \cdot 12}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ & = 16 \cdot 3 \cdot 7 \cdot 13 = 4.368 \end{align}$

2. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid laki-laki adalah $495$. (SALAH)
   Akan dipilih $5$ murid laki-laki dari $12$ murid, dengan menggunakan aturan menggunakan Kombinasi dalam menyelesaikan masalah dapat kita peroleh:

   $\begin{align} C \left( n,r \right) & = \dfrac{n!}{r!(n-r)!} \\ C \left( 12,5 \right) & = \dfrac{12!}{5!(12-5)!} \\ & = \dfrac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7!}{5!(7)!} \\ & = \dfrac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ & = 11 \cdot 9 \cdot 8 = 792 \end{align}$

3. Banyaknya cara memilih sehingga terdapat tepat $2$ murid laki-laki sebagai pengurus inti adalah $36.960$. (BENAR)
   Akan dipilih $2$ murid laki-laki dari $12$ murid dan $3$ murid perempuan dari $16$ murid, dengan menggunakan aturan menggunakan Kombinasi dalam menyelesaikan masalah dapat kita peroleh:

   $\begin{align} C \left( 12,2 \right) \cdot C \left( 16,3 \right) & = \dfrac{12!}{5!(12-2)!} \cdot \dfrac{16!}{3!(16-3)!} \\ & = \dfrac{12 \cdot 11 \cdot 10!}{5!(10)!} \cdot \dfrac{16 \cdot 15 \cdot 14 \cdot 13!}{3!(13)!} \\ & = \dfrac{12 \cdot 11}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \cdot \dfrac{16 \cdot 15 \cdot 14}{3 \cdot 2 \cdot 1} \\ & = \left( 6 \cdot 11 \right) \cdot \left( 8 \cdot 5 \cdot 14 \right) \\ & = 36.960 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{Benar-Salah-Benar}$.

4. Soal Penalaran Matematika SNBT 2023

Dalam suatu kelas terdapat $12$ murid laki-laki dan $16$ murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah $80$. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada $4$ murid, dengan nilai masing-masing $52$, $56$, $62$, dan $66$, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik $7$ poin.

Akan dipilih pengurus inti kelas yang terdiri dari $5$ murid. Peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti adalah...

$(A)\ \dfrac{22}{36}$

$(B)\ \dfrac{47}{63}$

$(C)\ \dfrac{70}{117}$

$(D)\ \dfrac{88}{117}$

$(E)\ \dfrac{134}{273}$

Alternatif Pembahasan:

Peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti, dengan menggunakan Teori Peluang Kejadian Majemuk dan Cara Menggunakannya Menyelesaikan Soal Matematika kita perlukan banyak kemungkinan yang diharapkan $n(E)$ dan banyak kemungkinan yang terjadi $n(S)$.

Banyak kemungkinan yang yang diharapan satu atau dua murid laki-laki, jika kita jabarkan yang diharapkan adalah $1L$ dan $4P$ atau $2L$ dan $3P$, banyak kemungkinan adalah:
$\begin{align} n \left( E \right) & = C \left( 12,1 \right) \cdot C \left( 16,4 \right) + C \left( 12,2 \right) \cdot C \left( 16,3 \right) \\ n \left( E \right) & = \dfrac{12!}{1!(12-1)!} \cdot \dfrac{16!}{4!(16-4)!} + \dfrac{12!}{2!(12-2)!} \cdot \dfrac{16!}{3!(16-3)!} \\ & = \dfrac{12 \cdot 11!}{1!(11)!} \cdot \dfrac{16 \cdot 15 \cdot 14 \cdot 13 \cdot 12!}{4!(12)!} + \dfrac{12 \cdot 11 \cdot 19!}{2!(10)!} \cdot \dfrac{16 \cdot 15 \cdot 14 \cdot 13!}{3!(13)!} \\ & = 12 \cdot 4 \cdot 5 \cdot 7 \cdot 13 + 6 \cdot 11 \cdot 8 \cdot 5 \cdot 14 \end{align}$

Banyak kemungkinan yang mungkin terjadi dipilih $5$ murid dari $28$ murid, banyak kemungkinan adalah:
$\begin{align} n \left( S \right) & = C \left( 28,5 \right) \\ n \left( S \right) & = \dfrac{28!}{5!(28-5)!} \\ & = \dfrac{28 \cdot 27 \cdot 26 \cdot 25 \cdot 24 \cdot 23! }{5!(23)!} \\ & = \dfrac{28 \cdot 27 \cdot 26 \cdot 25 \cdot 24}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\ & = 28 \cdot 27 \cdot 26 \cdot 5 \end{align}$

Peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti adalah:
$\begin{align} P \left( E \right) & = \dfrac{ n \left( E \right)}{n \left( S \right)} \\ & = \dfrac{12 \cdot 4 \cdot 5 \cdot 7 \cdot 13 + 6 \cdot 11 \cdot 8 \cdot 5 \cdot 14}{28 \cdot 27 \cdot 26 \cdot 5} \\ & = \dfrac{12 \cdot 4 \cdot 5 \cdot 7 \cdot 13}{28 \cdot 27 \cdot 26 \cdot 5} + \dfrac{6 \cdot 11 \cdot 8 \cdot 5 \cdot 14}{28 \cdot 27 \cdot 26 \cdot 5} \\ & = \dfrac{2 \cdot 13}{ 9 \cdot 13} + \dfrac{11 \cdot 4}{9 \cdot 13} \\ & = \dfrac{26}{117} + \dfrac{44}{117} = \dfrac{70}{117} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ \dfrac{70}{117}$.

5. Soal Penalaran Matematika SNBT 2023

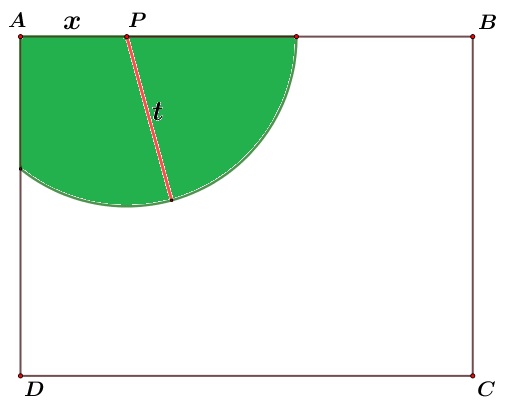
Kambing ditempatkan dalam kandang pada suatu halaman penuh rumput. Kandang berbentuk persegi panjang $ABCD$ dengan panjang $AB=12\ \text{meter}$ dan lebar $AD=9\ \text{meter}$. Kambing ditambatkan pada dinding $AB$ dengan tali yang panjangnya $t$ meter. Pangkal tali ditambatkan pada dinding $AB$ di titik $P$ berjarak $x$ meter dari titik sudut $A$.

Jika diketahui bahwa $0 \lt t \lt 6$ meter, daerah merumput kambing akan maksimal jika...

$(A)\ \frac{t}{2} \leq x \leq 6+\frac{t}{2}$

$(B)\ 6-t \leq x \leq 12-t$

$(C)\ \frac{t}{2} \leq x \leq 6+t$

$(D)\ t \leq x \leq 6+t$

$(E)\ t \leq x \leq 12-t$

Alternatif Pembahasan:

Agar daerah merumput kambing maskimum maka daerah yang rumput yang dihasilakan berupa setengah lingkaran seperti gambar berikut.

Agar terbetuk setengah lingkaran kemungkinan pertama $x \geq t$, karena jika $x \lt t$ maka titk $P$ akan semakin dekat dengan titik $A$ dan setengah lingkaran tidak akan terbentuk.

Kemungkinan kedua agar terbetuk setengah lingkaran adalah $x \leq 12-t$, karena jika $x \geq 12-t$ maka titk $P$ akan semakin dekat dengan titik $B$ dan setengah lingkaran tidak akan terbentuk.

dari kemungkinan $x \geq t$ dan $x \leq 12-t$ sederhananya dapat kita tulis menjadi $t \leq x \leq 12-t$

$\therefore$ Pilihan yang sesuai adalah $(E)\ t \leq x \leq 12-t$

6. Soal Penalaran Matematika SNBT 2023

Kambing ditempatkan dalam kandang pada suatu halaman penuh rumput. Kandang berbentuk persegi panjang $ABCD$ dengan panjang $AB=12\ \text{meter}$ dan lebar $AD=9\ \text{meter}$. Kambing ditambatkan pada dinding $AB$ dengan tali yang panjangnya $t$ meter. Pangkal tali ditambatkan pada dinding $AB$ di titik $P$ berjarak $x$ meter dari titik sudut $A$.

Misalkan $AP = x = 3$ dan panjang tali untuk kambing pertama adalah $t$ meter, $t \leq 9$. Kambing kedua ditempatkan dalam kandang diikat dengan tali yang ditambatkan ke titik $Q$ di dinding $BC$. Peternak kambing perlu meyakinkan bahwa kedua kambing tidak bertemu dan berebut rumput. Jika $BQ = 6$, panjang tali untuk kambing kedua tidak boleh lebih dari...meter.

$(A)\ \sqrt{72}-t$

$(B)\ \sqrt{117}-t$

$(C)\ \sqrt{131}-t$

$(D)\ \sqrt{145}-t$

$(E)\ \sqrt{180}-t$

Alternatif Pembahasan:

Titik $Q$ berada pada $BC$ dan $BQ=6$, sehingga panjang tali dari $P$ ke $Q$ dengan menggunakan Teorema Pythagoras adalah:
$\begin{align} PQ^{2} &= BP^{2}+BQ^{2} \\ PQ^{2} &= 9^{2}+6^{2} \\ PQ^{2} &= 81+36 \\ PQ^{2} &= 117 \\ PQ &= \sqrt{117} \end{align}$

Agar kambing dari $P$ dan dari $Q$ tidak bertemu maka panjang tali kambing kedua di $Q$ adalah panjang $PQ$ dikurang panjang tali kambing pertama yaitu $\sqrt{117}-t$.

$\therefore$ Pilihan yang sesuai adalah $(B)\ \sqrt{117}-t$

7. Soal Penalaran Matematika SNBT 2023

Kambing ditempatkan dalam kandang pada suatu halaman penuh rumput. Kandang berbentuk persegi panjang $ABCD$ dengan panjang $AB=12\ \text{meter}$ dan lebar $AD=9\ \text{meter}$. Kambing ditambatkan pada dinding $AB$ dengan tali yang panjangnya $t$ meter. Pangkal tali ditambatkan pada dinding $AB$ di titik $P$ berjarak $x$ meter dari titik sudut $A$.

Misalkan tali kambing pertama ditambatkan di titik $A$ dan tali kambing kedua di titik $C$. Panjang tali pertama adalah $t$ meter, dengan $6 \leq t \leq 9$. Jika panjang tali kambing kedua adalah maksimal sehingga kedua kambing tidak bertemu, jumlah luas daerah merumput kedua kambing akan mencapai nilai minimum untuk $t = \cdots$

$(A)\ 6$

$(B)\ 7$

$(C)\ 7,5$

$(D)\ 8,5$

$(E)\ 9$

Alternatif Pembahasan:

Kambing kedua pada titik $C$, sehingga jika panjang tali kambing kedua maksimal maka panjang tali agar kambing dapat bertemu panjang tali minimum adalah $AC$.

$\begin{align} AC^{2} &= AB^{2}+BC^{2} \\ AC^{2} &= 12^{2}+9^{2} \\ AC^{2} &= 144+91 \\ AC^{2} &= 225 \\ AC &= \sqrt{225}=15 \end{align}$
Dari panjang $AC$ di atas, agar kedua kambing tidak bertemu maka panjang tali kedua adalah $15-t$ dimana $6 \leq t \leq 9$.

Luas rumput yang terbentuk adalah berupa seperempat lingkaran, dimana jari-jari lingkaran pertama adalah $t$ dan jari-jari lingkaran kedua adalah $15-t$. Luas keseluruhan adalah:
$\begin{align} L_{t} &= L_{1}+L_{2} \\ L_{t} &= \frac{1}{4} \pi r_{1}^{2} + \frac{1}{4} \pi r_{2}^{2} \\ L_{t} &= \frac{1}{4} \pi \left( r_{1}^{2} + r_{2}^{2} \right) \\ &= \frac{1}{4} \pi \left( t^{2} + (15-t)^{2} \right) \\ &= \frac{1}{4} \pi \left( 2t^{2} -30t + 225 \right) \end{align}$

Luas minimum terjadi saat $L'_{t}=0$, sehingga kita peroleh:
$\begin{align} L_{t}' &= 0 \\ \frac{1}{4} \pi \left( 4t -30 \right) &= 0 \\ 4t -30 &= 0 \\ 4t &= 30 \\ t &= \frac{30}{4} = 7,5 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 7,5$

8. Soal Penalaran Matematika SNBT 2023

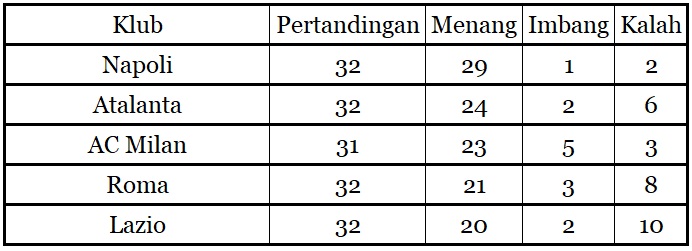
Liga Seri A Italia Berikut ini adalah tabel klasemen sementara lima klub teratas di Liga Seri $A$ Italia tahun $2022$. Setiap klub melakukan tepat dua pertandingan dengan setiap tim lain di mana terdapat $20$ klub yang bermain di Liga Seri A. Poin yang diberikan di bawah ini adalah setelah klub memainkan sekitar tiga puluh pertandingan.

Untuk setiap kemenangan, klub akan mendapatkan nilai $3$ poin, imbang $1$ poin, dan kalah $0$ poin.

Total banyaknya pertandingan di Liga Seri A Italia adalah... pertandingan.

$(A)\ 190$

$(B)\ 200$

$(C)\ 380$

$(D)\ 400$

$(E)\ 760$

Alternatif Pembahasan:

Pada sistem pertandingan seperti yang disampaikan seperti di atas dikenal dengan sistem kompetisi penuh. Dalam kompetisi penuh (bahasa Inggris: double round-robin), setiap peserta akan bertemu dengan peserta lainnya dua kali, biasanya satu pertemuan sebagai tuan rumah ("pertandingan kandang") dan satu pertemuan sebagai tamu ("pertandingan tandang").

Pada sistem kompetisi penuh, jika $n$ adalah banyaknya klub, suatu kompetisi penuh akan memerlukan $n \left( n-1 \right)$ pertandingan. Sehingga untuk $20$ klub Liga Seri $A$ Italia tahun $2022$ banyak pertandingan yang akan terjadi adalah $20 \left( 19 \right)=380$ pertandingan.

Apabila dengan proses pertandingan kita analisa perhitungan matematikanya dapat kita hituung dengan cara seperti berikut ini.

• Klub $1$ akan bertanding dengan $19$ klub lain sebanyak $2$ kali banyak pertandingan adalah $38$.
• Klub $2$ akan bertanding dengan $18$ klub lain (dengan klub $1$ sudah bertanding di atas) sebanyak $2$ kali banyak pertandingan adalah $36$.
• Klub $3$ akan bertanding dengan $17$ klub lain (dengan klub $1$ dan $2$ sudah bertanding di atas) sebanyak $2$ kali banyak pertandingan adalah $34$.
• $\vdots$
• Klub $19$ akan bertanding dengan $1$ klub lainnya sebanyak $2$ kali banyak pertandingan adalah $2$.

Total banyak pertandingan keselurhan adalah:
$\begin{align} & 38+36+34+32+\cdots+4+2\\ & =2 \left( 19+18+17+16+\cdots+2+1 \right)\\ & =2 \left( 190 \right)\\ &= 380 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 380$

9. Soal Penalaran Matematika SNBT 2023

Liga Seri A Italia Berikut ini adalah tabel klasemen sementara lima klub teratas di Liga Seri $A$ Italia tahun $2022$. Setiap klub melakukan tepat dua pertandingan dengan setiap tim lain di mana terdapat $20$ klub yang bermain di Liga Seri A. Poin yang diberikan di bawah ini adalah setelah klub memainkan sekitar tiga puluh pertandingan.

Untuk setiap kemenangan, klub akan mendapatkan nilai $3$ poin, imbang $1$ poin, dan kalah $0$ poin.

Poin minimal yang harus diperoleh Napoli di pertandingan tersisa untuk menjamin tim ini sebagai juara Liga Seri $A$ tahun $2022$ adalah...

$(A)\ 4$

$(B)\ 6$

$(C)\ 8$

$(D)\ 10$

$(E)\ 12$

Alternatif Pembahasan:

Banyak pertandingan yang dilakukan setiap klub adalah $38$ pertandingan.

1. Nilai Napoli dari tabel adalah $29(3) + 1(1) + 2(0) = 88$.
2. Nilai Atalanta dari tabel adalah $24(3) + 2(1) + 6(0) = 74$.
3. Nilai AC Milan dari tabel adalah $23(3) + 5(1) + 3(0) = 74$.

Apabila Atalanta pada sisa pertandingan sebanyak $6$ pertandingan menang semua maka nilainya menjadi $74+6 (3)=92$, sedangkan AC Milan pada sisa pertandingan sebanyak $7$ pertandingan menang semua maka nilainya menjadi $74+7 (3)=95$.

Agar Napoli berhasil menjadi juara nilai mereka lebih dari $95$, setidaknya $96$. Dari $6$ pertandingan sisa setidaknya Napoli minimal harus mendapat nilai $96-88=8$ poin.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 8$.

10. Soal Penalaran Matematika SNBT 2023

Liga Seri A Italia Berikut ini adalah tabel klasemen sementara lima klub teratas di Liga Seri $A$ Italia tahun $2022$. Setiap klub melakukan tepat dua pertandingan dengan setiap tim lain di mana terdapat $20$ klub yang bermain di Liga Seri A. Poin yang diberikan di bawah ini adalah setelah klub memainkan sekitar tiga puluh pertandingan.

Untuk setiap kemenangan, klub akan mendapatkan nilai $3$ poin, imbang $1$ poin, dan kalah $0$ poin.
Jika di pertandingan tersisa Atalanta memenangkan dua pertandingan dan sisanya imbang, kemungkinan komposisi menang – imbang – kalah untuk AC Milan pada pertandingan sisa untuk menjamin bahwa AC Milan menempati posisi kedua pada klasemen akhir adalah...
$(1)\ 3 – 3 – 1$
$(2)\ 3 – 2 – 2$
$(3)\ 3 – 4 – 0$
$(4)\ 3 – 0 – 4$

$(A)\ 1,2,3\ \text{Benar}$

$(B)\ 1,3\ \text{Benar}$

$(C)\ 2,4\ \text{Benar}$

$(D)\ 4\ \text{Saja Benar}$

$(E)\ \text{Semua Benar}$

Alternatif Pembahasan:

Banyak pertandingan yang dilakukan setiap klub adalah $38$ pertandingan.

1. Nilai Atalanta dari tabel adalah $24(3) + 2(1) + 6(0) = 74$.
2. Nilai AC Milan dari tabel adalah $23(3) + 5(1) + 3(0) = 74$.

Apabila Atalanta pada $6$ sisa pertandingan diperoleh $2$ menang dan $4$ imbang maka nilainya menjadi $74+2(3)+4(1)=84$.

Agar AC Milan menempati posisi kedua, dari $7$ sisa pertandingan mereka harus mengumpulkan nilai setidaknya $11$ poin.

Komposisi menang – imbang – kalah untuk AC Milan yang menghasilkan nilai paling sedikit $11$ adalah:
1. $3 – 3 – 1$, nilai yang terkumpul adalah $3(3)+ 3(1)+1(0)=12$.
2. $3 – 2 – 2$, nilai yang terkumpul adalah $3(3)+ 2(1)+2(0)=11$.
3. $3 – 4 – 0$, nilai yang terkumpul adalah $3(3)+ 4(1)+1(0)=13$.
4. $3 – 0 – 4$, nilai yang terkumpul adalah $3(3)+ 0(1)+4(0)=9$.

$\therefore$ Pilihan yang sesuai adalah $(A)\ 1,2,3\ \text{Benar}$.

Catatan Soal dan Pembahasan 10 Contoh Soal Penalaran Matematika UTBK-SNBT 2023 Dari Simulasi Tes BPPP Kemdikbud di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.

JADIKAN HARI INI LUAR BIASA!
Ayo Share (Berbagi) Satu Hal Baik.

Jika ingin sukses harus pintar, Jika ingin pintar maka harus belajar, dan Jika ingin belajar harus rajin membaca.

Nie Ing Han