Pembahasan 30 Soal Sistem Persamaan Linear Dua Variabel (SPLDV) Matematika SMP

Calon guru belajar matematika dasar SMP lewat soal dan pembahasan kesebangunan dan kekongruenan pada matematika SMP. Apa yang diharapkan setelah mempelajari materi ini, yaitu dapat menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar.

Soal matematika dasar kesebangunan dan kekongruenan untuk SMP kita pilih dari soal-soal yang sudah pernah diujikan pada soal Ujian Sekolah matematika SMP, soal Ujian Nasional matematika SMP, atau soal ujian seleksi akademik masuk SMA Unggulan atau SMA Plus.

---

KESEBANGUNAN

Dua buah bangun dikatakan sebangun (kecuali lingkaran) apabila:

1. Besar sudut yang seletak atau bersesuaian sama besar.
2. Perbandingan panjang sisi yang seletak atau bersesuaian adalah sebanding.

Sebangun disimbolkan dengan $\sim$, misalkan $\bigtriangleup ABC$ sebangun dengan $\bigtriangleup PQR$ dapat dituliskan dengan $\bigtriangleup ABC \sim \bigtriangleup PQR$.

Karena $\angle A=\angle P$ dan $\angle B=\angle Q$ maka $\bigtriangleup ABC$ sebangun dengan $\bigtriangleup PQR$ dan dapat dituliskan $\bigtriangleup ABC \sim \bigtriangleup PQR$.

Akibat dari kesebangunan maka diperoleh perbandingan sisi-sisi yang bersesuaian sama besar. Jika kita gunakan segitiga di atas sebagai pedoman, maka kita peroleh;
\begin{align} \dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AC}{PR} \end{align}

---

KEKONGRUENAN

Dua buah bangun dikatakan kongruen apabila:

1. Besar sudut yang seletak atau bersesuaian sama besar.
2. Panjang sisi yang seletak atau bersesuaian ukurannya sama.

Dengan kata lain dua bangun dikatakan kongruen jika ukuran dan bentuknya sama. Kongruen disimbolkan dengan $\cong$, misalkan $\bigtriangleup ABC$ kongruen dengan $\bigtriangleup PQR$ dapat dituliskan dengan $\bigtriangleup ABC \cong \bigtriangleup PQR$.

---

CIRI-CIRI DUA SEGITIGA KONGRUEN

Dua buah segitiga dapat dikatakan kongruen jika dipenuhi salah satu dari ciri berikut ini:

1. Panjang sisi-sisi kedua segitiga adalah sama. Dapat diingat dengan ciri "sisi-sisi-sisi".
   
   
2. Dua sisi segitiga yang bersesuaian mempunyai ukuran yang sama dan membentuk sudut yang sama besar. Dapat diingat dengan ciri "sisi-sudut-sisi".
   
   
3. Dua sudut segitiga yang bersesuaian sama besar dan sisi yang letaknya diantara kedua sudut sama ukurannya sama. Dapat diingat dengan ciri "sudut-sisi-sudut".
   
   

---

Pembahasan Soal Kesebangunan Dan Kekongruenan Matematika SMP

Untuk menambah pemahaman kita terkait Kesebangunan Dan Kekongruenan, mari kita simak beberapa soal latihan di bawah ini. Soal latihan kita pilih dari soal-soal yang diujikan pada Ujian Nasional matematika SMP atau Ujian Sekolah matematika SMP.

Soal latihan Kesebangunan Dan Kekongruenan berikut ini, silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan Periksa Jawaban dan jika hasilnya belum memuaskan, pilih Ulangi Tes untuk tes ulang.

Ayo dicoba terlebih dahulu, Sebelum melihat pembahasan soal.
Tunjukkan Kemampuan Terbaikmu!

Nama Peserta :
Tanggal Tes :
Jumlah Soal :	38 soal

Petunjuk Pengerjaan Soal:
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.

1. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Pada gambar berikut, segitiga $PQR$ dan segitiga $STU$ merupakan sua segitiga kongruen. Besar $\angle R=\angle U$ dan $\angle Q=\angle S$. Manakah pasangan sisi yang sama panjang?

...

$(A)\ PR=SU $

$(B)\ QR=TU $

$(C)\ PQ=SU $

$(D)\ PQ=ST $

Alternatif Pembahasan:

Jika kita gambarkan dengan menambahkan informasi yang ada pada soal, maka gambar segitiga akan tampak seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan $\angle R=\angle U$, $\angle Q=\angle S$, $\angle P=\angle T$.

Dari informasi sudut pada segitiga di atas dapat kita peroleh sisi yang sama panjang yaitu sisi di depan sudut yang sama besar, $PR=TU$, $PQ=ST$, dan $QR=US$

$\therefore$ Pilihan yang sesuai adalah $(D)\ PQ=ST$

2. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Sebuah pohon yang berada di depan gedung mempunyai tinggi $8\ \text{m}$. Pada saat yang sama bayangan gedung berimpit dengan bayangan pohon seperti tampak pada gambar di bawah.

Tinggi gedung yang sesuai ukuran tersebut adalah....

$(A)\ 5,30\ \text{m} $

$(B)\ 6,25\ \text{m} $

$(C)\ 10,00\ \text{m} $

$(D)\ 12,00\ \text{m} $

Alternatif Pembahasan:

Jika kita misalkan titik-titik penting pada gambar kita beri nama seperti berikut ini;

Dari gambar di atas kita peroleh bahwa $\bigtriangleup ABC$ sebangun dengan $\bigtriangleup ADE$, sehingga berlaku:
$\begin{align}
\dfrac{AB}{AD} &= \dfrac{BC}{DE} \\
\dfrac{10}{15} &= \dfrac{8}{DE} \\
DE &= \dfrac{8 \times 15}{10} \\
DE &= 12
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 12,00\ \text{m}$

3. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Perhatikan gambar

Panjang $BC$ adalah....

$(A)\ \sqrt{16}\ \text{cm} $

$(B)\ \sqrt{48}\ \text{cm} $

$(C)\ \sqrt{64}\ \text{cm} $

$(D)\ \sqrt{192}\ \text{cm} $

Alternatif Pembahasan:

Pada gambar terdapat tiga segitiga siku-siku, kita ilustrasikan seperti berikut ini:

Dari gambar di atas kita peroleh tiga segitiga siku-siku yang sebangun, sehingga berlaku:
$\begin{align}
\dfrac{AC}{AB} & = \dfrac{AD}{AC} \\
\dfrac{AC}{16} & = \dfrac{4}{AC} \\
AC^{2} & = 64 \\
AC & = 8 \\
\hline
BC^{2} & = AB^{2}-AC^{2} \\
& = 16^{2}-8^{2} \\
& = 256 -64 \\
BC & = \sqrt{192}
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ \sqrt{192}\ \text{cm}$

4. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Perhatikan gambar

Seseorang akan mengukur lebar sungai dengan cara menancapkan tongkat $A,B,C, \text{dan}\ D$ seperti pada gambar. Tongkat $A$ segaris dengan pohon $E$ diseberang sungai. Jika $AB=12\ \text{m}$, $BD=15\ \text{m}$ dan $CD=25\ \text{m}$, lebar sungai adalah...

$(A)\ 15\ m $

$(B)\ 20\ m $

$(C)\ 31\ m $

$(D)\ 35\ m $

Alternatif Pembahasan:

Dari gambar di atas, $\bigtriangleup ABE$ sebangun dengan $\bigtriangleup BCD$ karena $\angle BAE=\angle BDC$ dan $\angle ABE=\angle CBD$, sehingga berlaku:
$\begin{align}
\dfrac{AB}{BD} &= \dfrac{AE}{CD} \\
\dfrac{12}{15} &= \dfrac{AE}{25} \\
\dfrac{4}{5} \times 25 &= AE \\
20 &= AE
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 20\ \text{m} $

5. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap

Pada gambar berikut, segitiga $KLM$ kongruen dengan segitiga $RST$.
Pernyataan yang sama panjang adalah...

$(A)\ KL=ST $

$(B)\ LM=RS $

$(C)\ KM=RT $

$(D)\ KL=RT $

Alternatif Pembahasan:

Segitiga $KLM$ dan $RST$ kongruen, maka:

• $\angle K=\angle R=75^{\circ}$
• $\angle L=\angle S=35^{\circ}$
• $\angle M=\angle T=70^{\circ}$
• $KM=RT$
• $ML=TS$
• $KL=RS$

$\therefore$ Pilihan yang sesuai adalah $(C)\ KM=RT$

6. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap

Perhatikan gambar berikut!

Jika $AB = BC = CD$. maka panjang $BF$ adalah...

$(A)\ 4\ \text{cm} $

$(B)\ 4,5\ \text{cm} $

$(C)\ 5\ \text{cm} $

$(D)\ 5,5\ \text{cm} $

Alternatif Pembahasan:

Pada gambar ada simbol arah tanda panah, garis yang ada arah tanda panah artinya adalah garis yang sejajar.
Garis $AB$ sejajar dengan garis $CD$ dan garis $CB$ sejajar dengan garis $ED$.

Untuk mendapatkan panjang garis $BF$, kita coba gunakan garis bantu, ilustrasinya kurang lebih seperti berikut ini;

Dari gambar di atas kita perhatikan $\bigtriangleup\ ABF$ dan $\bigtriangleup\ AGE$ adalah segitiga yang sebangun, maka berlaku;
$\begin{align}
\frac{BF}{GE} & = \frac{AB}{AG} \\
\frac{BF}{10} & = \frac{7}{14} \\
BF & = \frac{1}{2} \times 10 \\
BF & = 5
\end{align}$

$\therefore$ Panjang $BF$ adalah $(C)\ 5\ \text{cm}$

7. Soal UNBK Matematika SMP 2018 |*Soal Lengkap

Berdasar gambar di bawah, segitiga $ABC$ dan $PQR$ kongruen.
Pernyataan yang salah adalah...

$(A)\ AC=QR $

$(B)\ AB=PQ $

$(C)\ \angle B=\angle P $

$(D)\ \angle Q=\angle B $

Alternatif Pembahasan:

Segitiga $ABC$ dan $PQR$ kongruen, maka:

• $\angle A=\angle Q=55^{\circ}$
• $\angle B=\angle P=50^{\circ}$
• $\angle C=\angle R=75^{\circ}$
• $AB=PQ$
• $AC=QR$
• $BC=PR$

$\therefore$ Pilihan yang sesuai adalah $(D)\ \angle Q=\angle B$

8. Soal UNBK Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar berikut!

Panjang $AB = BC = CD$. Jika panjang $AB = 7\ \text{cm}$ dan panjang $DE = 3\ \text{cm}$, maka panjang $BF$ adalah...

$(A)\ 5,0\ \text{cm} $

$(B)\ 5,5\ \text{cm} $

$(C)\ 6,0\ \text{cm} $

$(D)\ 6,5\ \text{cm} $

Alternatif Pembahasan:

Pada gambar ada simbol arah tanda panah, garis yang ada arah tanda panah artinya adalah garis yang sejajar.
Garis $AB$ sejajar dengan garis $CD$ dan garis $CB$ sejajar dengan garis $ED$.

Untuk mendapatkan panjang garis $BF$, kita coba gunakan garis bantu, ilustrasinya kurang lebih seperti berikut ini;

Dari gambar di atas kita perhatikan $\bigtriangleup\ ABF$ dan $\bigtriangleup\ AGE$ adalah segitiga yang sebangun, maka berlaku;
$\begin{align}
\frac{BF}{GE} & = \frac{AB}{AG} \\
\frac{BF}{10} & = \frac{7}{14} \\
BF & = \frac{1}{2} \times 10 \\
BF & = 5
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 5,0\ \text{cm}$

9. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar berikut!

Sebidang tanah berbentuk trapesium samakaki. Di bagian dalam akan dibuat kolam ikan yang sebangun dengan tanah tersebut. Di sekeliling kolam dibangun jalan setapak. Luas jalan tersebut adalah...

$(A)\ 216\ \text{m}^{2} $

$(B)\ 226\ \text{m}^{2} $

$(C)\ 236\ \text{m}^{2} $

$(D)\ 316\ \text{m}^{2} $

Alternatif Pembahasan:

Untuk menghitung luas jalan, kita coba hitung dari luas tanah dan luas kolam. Bentuk tanah dan kolam sama-sama berbentuk trapesium sama kaki sehingga kedua trapesium adalah trapesium yang sebangun. Sehingga berlaku:
$\begin{align} \dfrac{x}{15} &=\dfrac{36}{y} =\dfrac{20}{25} \\ \dfrac{x}{15} &=\dfrac{36}{y} =\dfrac{4}{5} \\ \hline \dfrac{x}{15} &=\dfrac{4}{5} \\ x &= \dfrac{4}{5} \times 15 \\ x &=12 \\ \hline \dfrac{36}{y} &= \dfrac{4}{5} \\ y &= \dfrac{5}{4} \times 36 \\ y &= 45 \end{align}$

Untuk mendapatkan luas jalan, kita bisa dapat dari selisih luas tanah dengan luas kolam.

Dengan memperhatikan data-data pada gambar dapat kita peroleh:

• Luas Tanah
  $\begin{align}
  L_{t}\ &= \dfrac{1}{2} \times (15+45) \times 20 \\ &= \dfrac{1}{2} \times 60 \times 20 \\ &= 600\ \text{m}^{2} \end{align}$
• Luas Kolam
  $\begin{align}
  L_{k}\ &= \dfrac{1}{2} \times (12+36) \times 16 \\ &= \dfrac{1}{2} \times 48 \times 16 \\ &= 384\ \text{m}^{2} \end{align}$
• Luas jalan adalah selisih luas tanah dengan luas kolam yaitu:
  $\begin{align}
  L_{j}\ &= L_{t}-L_{k} \\ &= 600\ \text{m}^{2} - 384\ \text{m}^{2}\\ &= 216\ \text{m}^{2} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 216\ \text{m}^{2}$

10. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

"Lebar Sungai"
Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat pada posisi $A$, $B$, $C$, dan $D$ dengan ukuran seperti gambar.

Andi ingin mengukur lebar sungai dari tongkat $D$ sampai pohon. Berapa lebar sungai tersebut?

$(A)\ 11\ \text{m} $

$(B)\ 12\ \text{m} $

$(C)\ 15\ \text{m} $

$(D)\ 16\ \text{m} $

Alternatif Pembahasan:

Untuk menghitung lebar sungai dengan informasi yang ada pada soal, kita coba gunakan perbandingan sisi yang bersesuaian pada segitiga.

Kita misalkan lebar sungai adalah $x$ dan posisi pohon adalah $P$.
Dengan demikian kita peroleh $2$ segitiga yang sebangun yaitu $\bigtriangleup ABP$ dan $\bigtriangleup DCP$.
$ \begin{array}
& \dfrac{AB}{DC} =\dfrac{AP}{DP} \\ & \dfrac{8}{6} = \dfrac{4+x}{x} \\ & 8x = 6(4+x) \\ & 8x = 24+6x \\ & 8x-6x = 24 \\ & 2x = 24 \\ & x = \frac{24}{2} \\ & x = 12
\end{array} $

$\therefore$ Pilihan yang sesuai adalah $(B)\ 12\ \text{m}$

11. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2005 |*Soal Lengkap

Suatu pohon yang tingginya $24\ \text{m}$ mempunyai bayangan di tanah sepanjang $18\ \text{m}$. Jika pohon pinus yang tinginya $60\ \text{m}$, maka bayangannya di tanah sepanjang...

$(A)\ 40\ \text{m} $

$(B)\ 45\ \text{m} $

$(C)\ 75\ \text{m} $

$(D)\ 80\ \text{m} $

Alternatif Pembahasan:

Dengan menggunakan konsep perbandingan senilai maka kita peroleh:
$\begin{align}
\dfrac{t_{\text{pohon}}}{t_{\text{pinus}}} & = \dfrac{\text{bayangan}_{\text{pohon}}}{\text{bayangan}_{\text{pinus}}} \\ \dfrac{24}{60} & = \dfrac{18}{\text{bayangan}_{\text{pinus}}} \\ \text{bayangan}_{\text{pinus}} \times 24 & = 18 \times 60 \\ \text{bayangan}_{\text{pinus}} & = \dfrac{18 \times 60}{24} \\ \text{bayangan}_{\text{pinus}} & = 45
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 45\ \text{m}$

12. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2005 |*Soal Lengkap

Segitiga $ABC$ seperti pada gambar di bawah ini:

$DE$ sejajar $AB$
$AB=5$, $DE=3$, $CE=x$ dan $EB=y$.
Perbandingan $x:y=\cdots$...

$(A)\ 5:4 $

$(B)\ 3:4 $

$(C)\ 2:3 $

$(D)\ 3:2 $

Alternatif Pembahasan:

Dari gambar kita peroleh informasi bahwa $\bigtriangleup CDE$ sebangun dengan $\bigtriangleup CAB$ sehingga berlaku:
$\begin{align}
\dfrac{DE}{AB} & = \dfrac{CE}{CB} \\ \dfrac{3}{5} & = \dfrac{x}{x+y} \\ 3(x+y) & = 5x \\ 3x+3y & = 5x \\ 3y & = 5x-3x \\ 3y & = 2x \\ \dfrac{x}{y} & = \dfrac{3}{2}
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 3:2$

13. Soal UN Matematika SMP 2018 |*Soal Lengkap

Dua segitita pada gambar di bawah ini adalah kongruen.

Pasangan sisi yang sama panjang adalah...

$(A)\ AB\ \text{dan}\ EC $

$(B)\ AD\ \text{dan}\ BE $

$(C)\ AC\ \text{dan}\ CD $

$(D)\ BC\ \text{dan}\ CD $

Alternatif Pembahasan:

Dari informasi pada gambar garis $AB$ sejajar dengan garis $ED$ sehingga besar sudur yang sama adalah $\angle ACB=\angle ECD$, $\angle ABC=\angle CDE$ dan $\angle BAC=\angle CED$. Jika kita gambarkan dapat seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Dari informasi sudut pada segitiga di atas dapat kita peroleh sisi yang sama panjang yaitu sisi di depan sudut yang sama besar, $BA=ED$, $AC=CE$, dan $BC=CD$

$\therefore$ Pilihan yang sesuai adalah $(D)\ BC\ \text{dan}\ CD$

14. Soal UN Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar!

Diketahui $AB = BC = CD$. Panjang $BF$ adalah...

$(A)\ 17\ \text{cm} $

$(B)\ 16\ \text{cm} $

$(C)\ 15\ \text{cm} $

$(D)\ 14\ \text{cm} $

Alternatif Pembahasan:

Pada gambar ada simbol arah tanda panah, garis yang ada arah tanda panah artinya adalah garis yang sejajar.
Garis $AB$ sejajar dengan garis $CD$ dan garis $BC$ sejajar dengan garis $DE$.

Untuk mendapatkan panjang garis $BF$, kita coba gunakan garis bantu, ilustrasinya kurang lebih seperti berikut ini;

Dari gambar di atas kita perhatikan $\bigtriangleup ABF$ dan $\bigtriangleup AGE$ adalah segitiga yang sebangun, maka berlaku;
$\begin{align}
\dfrac{BF}{GE} & = \dfrac{AB}{AG} \\
\dfrac{BF}{30} & = \dfrac{18}{36} \\
BF & = \dfrac{1}{2} \times 30 \\
BF & = 15
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 15\ \text{cm}$

15. Soal UN Matematika SMP 2017 |*Soal Lengkap

Diketahui segitiga $ABC$ dan $KLM$ kongruen. Besar $\angle KLM=62^{\circ}$, $\angle MKL=48^{\circ}$, $\angle ABC=62^{\circ}$, dan $\angle ACB=70^{\circ}$. Pasangan sisi yang sama panjang pada kedua segitiga itu adalah...

$(A)\ AC=LM $

$(B)\ AB=KM $

$(C)\ BC=LM $

$(D)\ BC=KM $

Alternatif Pembahasan:

Dari informasi pada soal jika kita gambarkan dapat seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Dari informasi sudut pada segitiga di atas dapat kita peroleh sisi yang sama panjang yaitu sisi di depan sudut yang sama besar, $BC=LM$, $AC=KM$, dan $AB=LK$

$\therefore$ Pilihan yang sesuai adalah $(C)\ BC=LM$

16. Soal UN Matematika SMP 2017 |*Soal Lengkap

Perhatikan gambar berikut!

Bangun $ABCD$ dan bangun $AEFG$ sebangun. Luas bangun $ABCD$ adalah...

$(A)\ 162,0\ \text{cm} $

$(B)\ 202,5\ \text{cm} $

$(C)\ 324,0\ \text{cm} $

$(D)\ 405,0\ \text{cm} $

Alternatif Pembahasan:

Untuk menghitung luas bangun $ABCD$, kita perlu dapat tinggi dari bangun $AEFG$ yaitu $AG$ atau $FH$.
$\begin{align}
FH^{2} & = 10^{2}-6^{2} \\ FH^{2} & = 100-36 \\ FH^{2} & = 64 \\ FH & = \sqrt{64}=8 \end{align}$

Bangun $ABCD$ dan bangun $AEFG$ sebangun, sehingga berlaku:
$\begin{align}
\dfrac{AG}{AD} & = \dfrac{FE}{CB} \\ \dfrac{8}{AD} & = \dfrac{10}{15} \\ AD & = \dfrac{8 \times 15}{10} = 12 \\ \hline \dfrac{AG}{AD} & = \dfrac{AE}{AB} \\ \dfrac{8}{12} & = \dfrac{12}{AB} \\ AB & = \dfrac{12 \times 12}{8}= 18 \\ \hline \dfrac{AG}{AD} & = \dfrac{GF}{DC} \\ \dfrac{8}{12} & = \dfrac{6}{DC} \\ DC & = \dfrac{12 \times 6}{8}=9 \\ \end{align}$

Luas $ABCD$ adalah:
$\begin{align} L & = \dfrac{1}{2} \times (AB+DC) \times AD \\ & = \dfrac{1}{2} \times ( 18 + 9) \times 12 \\ & = 27 \times 6 \\ & = 162 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 162,0\ \text{cm}$

17. Soal UN Matematika SMP 2017 |*Soal Lengkap

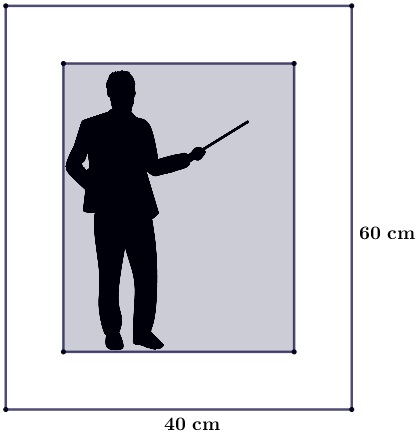
Sebuah foto ditempelkan pada selembar karton. Di sebelah atas, kiri, dan kanan foto masih tersisa karton selebar $3\ \text{cm}$. Jika foto dan karton sebangun, luas karton yang tidak tertutup adalah...

$(A)\ 1.200\ \text{cm}^{2} $

$(B)\ 864\ \text{cm}^{2} $

$(C)\ 728\ \text{cm}^{2} $

$(D)\ 666\ \text{cm}^{2} $

Alternatif Pembahasan:

Disampaikan pada soal di sebelah atas, kiri, dan kanan foto masih tersisa karton selebar $3\ \text{cm}$, sedangkan pada bagian bawah belum diketahui. Sehingga apabila kita gambarkan ukurannya dapat seperti berikut ini.

Foto dan karton sebangun, sehingga berlaku:
$\begin{align}
\dfrac{40}{34} & = \dfrac{60}{57-x} \\ \dfrac{2}{34} & = \dfrac{3}{57-x} \\ (2)(57-x) & = (3)(34) \\ 114-2x & = 102 \\ -2x & = 102-114 \\ -2x & = -12\ \longrightarrow x=6 \end{align}$

Luas karton tidak tertutup foto adalah:
$\begin{align}
L & = L_{\text{karton}}-L_{\text{foto}} \\ & = 40 \times 60 - 34 \times 51 \\ & = 2.400 -1.734 \\ & = 666 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 666\ \text{cm}^{2}$

18. Soal UN Matematika SMP 2017 |*Soal Lengkap

Perhatikan gambar sketsa kebun berikut!

Sebidang kebun berbentuk jajargenjang. Di bagian dalam kebun dibuat taman dengan panjang $AB=20\ \text{m}$ dan panjang $DE=15\ \text{m}$. Di sekeliling taman dibuat jalan. Jika kebun dan taman sebangun, luas jalan adalah...

$(A)\ 66\ \text{m}^{2} $

$(B)\ 132\ \text{m}^{2} $

$(C)\ 300\ \text{m}^{2} $

$(D)\ 360\ \text{m}^{2} $

Alternatif Pembahasan:

Disampaikan pada soal di kiri dan kanan kebun ada jalan selebar $2\ \text{m}$ sedangkan pada bagian atas dan bawah belum diketahui. Sehingga apabila kita gambarkan ukurannya dapat seperti berikut ini.

Kebun dan taman sebangun, sehingga berlaku:
$\begin{align}
\dfrac{20}{15} & = \dfrac{24}{15+2x} \\ (20)(15+2x) & = (15)(24) \\ 300+40x & = 360 \\ 40x & = 360-300 \\ 40x & = 60\ \longrightarrow x=1,5 \end{align}$

Luas jalan adalah:
$\begin{align}
L & = L_{\text{kebun}}-L_{\text{taman}} \\ & = (20+2+2) \times (15+1,5+1,5) - 20 \times 15 \\ & = 24 \times 18 - 20 \times 15 \\ & = 432 - 300 \\ & = 132 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 132\ \text{m}^{2}$

19. Soal UN Matematika SMP 2015 |*Soal Lengkap

Perhatikan gambar!

Trapesium $PQBA$ sebangun dengan $ABRS$. Jika $QB:BR=3:4$, panjang $SR$ adalah...

$(A)\ 32\ \text{cm} $

$(B)\ 30\ \text{cm} $

$(C)\ 25\ \text{cm} $

$(D)\ 24\ \text{cm} $

Alternatif Pembahasan:

Trapesium $PQBA$ sebangun dengan $ABRS$, sehingga berlaku:
$\begin{align}
\dfrac{PQ}{AB} & = \dfrac{QB}{BR} \\ \dfrac{PQ}{AB} & = \dfrac{3}{4} \\ \dfrac{18}{AB} & = \dfrac{3}{4} \\ AB & = \dfrac{18 \times 4}{3}=24 \end{align}$

Untuk menghitung panjang $AB$ seperti gambar dapat kita gunakan aturan:
$\begin{align}
AB & = \dfrac{QB \times SR + BR \times PQ}{QB+BR} \\ 24 & = \dfrac{3 \times SR + 4 \times 18}{3+4} \\ 24 & = \dfrac{3SR+ 72}{7} \\ 24 \times 7 & = 3SR+ 72 \\ 168-72 & = 3SR \\ 96 & = 3SR\ \longrightarrow SR=\dfrac{96}{3}=32 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 32\ \text{cm}$

20. Soal UN Matematika SMP 2015 |*Soal Lengkap

Diketahui $\bigtriangleup DEF$ dan $\bigtriangleup PQR$ sebangun, panjang $DE=9\ \text{cm}$, $EF=12\ \text{cm}$, $DF=6\ \text{cm}$, $PQ=15\ \text{cm}$, $PR=10\ \text{cm}$, dan $QR=20\ \text{cm}$. Perbandingan sisi-sisi pada kedua segitiga tersebut adalah...

$(A)\ 3:4 $

$(B)\ 3:5 $

$(C)\ 4:5 $

$(D)\ 9:10 $

Alternatif Pembahasan:

Untuk mempermudah soal di atas, kita coba menggambarkannya terlebih dahulu,

Karena $\bigtriangleup DEF \sim \bigtriangleup PQR $ maka perbandingan sisi-sisi yang bersesuaian sama besar. Dengan bantuan gambar di atas kita peroleh persamaan sebagai berikut;
\begin{align} \dfrac{PR}{DF} &=\dfrac{PQ}{DE}=\dfrac{QR}{EF} \\ \dfrac{10}{6} &=\dfrac{15}{9}=\dfrac{20}{12} \\ \dfrac{10}{6} &=\dfrac{15}{9}=\dfrac{20}{12} \end{align}

Alternatif lain, dapat dengan melihat pola sisi pada $\bigtriangleup DEF$ yaitu $6,9,12$ sedangkan pada $\bigtriangleup PQR$ adalah $10,15,20$.
Karena $\bigtriangleup DEF$ dan $\bigtriangleup PQR$ sebangun maka perbandingan sisi-sisi yang bersesuaian sama besar yaitu $\dfrac{6}{10}=\dfrac{9}{15}=\dfrac{12}{20}=\dfrac{3}{5}$.

$\therefore$ Pilihan yang sesuai adalah $(B)\ 3:5$

21. Soal UN Matematika SMP 2015 |*Soal Lengkap

Panjang bayangan sebuah menara $15\ \text{m}$ dan pada saat yang sama sebuah tiang pancang memiliki bayangan $3\ \text{m}$. Jika tinggi tiang pancang $7\ \text{m}$, maka tinggi menara adalah...

$(A)\ 19\ \text{meter} $

$(B)\ 22\ \text{meter} $

$(C)\ 25\ \text{meter} $

$(D)\ 35\ \text{meter} $

Alternatif Pembahasan:

Jika kita gambarkan, menara dan pancang dapat seperti berikut ini;

Dari ilustrasi di atas, dapat kita tarik kesimpulan bahwa pancang dan bayangannya sebangun dengan menara dan bayangannya sehingga berlaku:
$\begin{align} \dfrac{\text{Tinggi Menara}}{\text{Tinggi Pancang}} &= \dfrac{\text{Bayangan Menara}}{\text{Bayangan Pancang}} \\ \dfrac{\text{Tinggi Menara}}{7} &= \dfrac{15}{3} \\ \text{Tinggi Menara} &= 5 \times 5 \\ &= 25 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 25\ \text{meter}$

22. Soal UN Matematika SMP 2015 |*Soal Lengkap

Perhatikan gambar!

Perbandingan yang benar adalah...

$(A)\ \dfrac{DE}{AE}\ \text{dan}\ \dfrac{CD}{AB} $

$(B)\ \dfrac{CE}{AE}\ \text{dan}\ \dfrac{CD}{AB} $

$(C)\ \dfrac{CD}{AB}\ \text{dan}\ \dfrac{AE}{BE} $

$(D)\ \dfrac{CD}{AB}\ \text{dan}\ \dfrac{AE}{DE} $

Alternatif Pembahasan:

Dari informasi pada gambar garis $AB$ sejajar dengan garis $CD$ sehingga besar sudut yang sama adalah $\angle BEA=\angle CED$, $\angle BAE=\angle ECD$ dan $\angle ABC=\angle EDC$. Jika kita gambarkan dapat seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Dari informasi sudut pada segitiga di atas dapat kita peroleh perbandingan sisi yang bersesuaian adalah sisi di depan sudut yang sama besar, $\dfrac{BA}{CD}=\dfrac{EB}{ED}=\dfrac{AE}{EC}$ atau $\dfrac{CD}{BA}=\dfrac{ED}{EB}=\dfrac{EC}{AE}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ \dfrac{CE}{AE}\ \text{dan}\ \dfrac{CD}{AB}$

23. Soal UN Matematika SMP 2014 |*Soal Lengkap

Perhatikan gambar jajargenjang di bawah ini!

Banyak pasangan segitiga yang kongruen adalah...

$(A)\ 4 $

$(B)\ 5 $

$(C)\ 6 $

$(D)\ 7 $

Alternatif Pembahasan:

Dari informasi pada gambar, pasangan segitiga yang kongruen antara lain:

1. $\bigtriangleup ABD \cong \bigtriangleup BCD$
2. $\bigtriangleupABC \cong \bigtriangleup ACD$
3. $\bigtriangleup AOB \cong \bigtriangleup COD$
4. $\bigtriangleup AOD \cong \bigtriangleupBOC$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 4$

24. Soal UN Matematika SMP 2014 |*Soal Lengkap

Perhatikan gambar!

Panjang $CE$ adalah...

$(A)\ 10\ \text{cm} $

$(B)\ 8\ \text{cm} $

$(C)\ 7\ \text{cm} $

$(D)\ 6\ \text{cm} $

Alternatif Pembahasan:

Pada $\bigtriangleup CDE$ sebangun dengan $\bigtriangleup ABC$ karena dua sudut segitiga tersebut sama besar yaitu $\angle ABC = \angle CDE$ dan $\angle ACB = \angle DCE$. Karena kedua segitiga sebangun maka berlaku:
$\begin{align}
\dfrac{CE}{AC} & = \dfrac{DE}{AB} \\ \dfrac{CE}{8+7} & = \dfrac{8}{12} \\ \dfrac{CE}{15} & = \dfrac{2}{3} \\ CE & = \dfrac{2 \times 15}{3}=10 \end{align}$

Catatan!
Untuk membandingkan sisi-sisi yang bersesuaian pada bidang yang sebangun, dapat memperhatikan perbandingan sisi di depan sudut yang sama besar.
Pada soal di atas, sisi di depan sudut $x$ adalah $CE$ dan $AC$, sisi di depan sudut $C$ adalah $DE$ dan $AB$ sehingga perbandingan $\dfrac{CE}{AC} = \dfrac{DE}{AB}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 10\ \text{cm}$

25. Soal UN Matematika SMP 2013 |*Soal Lengkap

Diketahui segitiga $\bigtriangleup PQR$ kongruen dengan $\bigtriangleup KLM$. Besar $\angle P=\angle L$ dan $\angle R=\angle K$. Pasangan sisi yang sama panjang adalah...

$(A)\ QR=LM $

$(B)\ PQ=KM $

$(C)\ QR=KM $

$(D)\ PR=KM $

Alternatif Pembahasan:

Dari informasi pada soal jika kita gambarkan dapat seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Untuk melihat sisi-sisi yang sama pada bidang yang kongruen, dapat memperhatikan panjang sisi di depan sudut yang sama besar. Pada gambar di atas berlaku:

• sisi di depan $\angle P$ adalah $QR$, sisi di depan $\angle L$ adalah $KM$ dan $\angle P=\angle L$ maka $QR=KM$.
• sisi di depan $\angle R$ adalah $PQ$, sisi di depan $\angle K$ adalah $ML$ dan $\angle R=\angle K$ maka $PQ=ML$.
• sisi di depan $\angle Q$ adalah $PR$, sisi di depan $\angle M$ adalah $KL$ dan $\angle Q=\angle M$ maka $PR=KL$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ QR=KM$

26. Soal UN Matematika SMP 2013 |*Soal Lengkap

Diketahui segitiga $ABC$ yang panjang sisinya $10\ \text{cm}$, $24\ \text{cm}$, dan $26\ \text{cm}$ sebangun dengan segitiga $PQR$ yang panjang sisinya $25\ \text{cm}$, $60\ \text{cm}$, dan $65\ \text{cm}$. Perbandingan panjang sisi segitiga $ABC$ dan segitiga $PQR$ adalah...

$(A)\ 1:5 $

$(B)\ 2:5 $

$(C)\ 5:2 $

$(D)\ 5:1 $

Alternatif Pembahasan:

Perbandingan panjang sisi segitiga $ABC$ dan segitiga $PQR$ dimana kedua segitiga adalah sebangun dapat kita lihat dari pola panjang sisi segitiga yang bersesuaian.

Pada segitiga segitiga $ABC$ panjang sisinya adalah $10,\ 24,\ 26$, sedangkan pada segitiga $PQR$ panjang sisinya $25,\ 60,\ 65$ sehingga perbandingan panjang sisi adalah $\dfrac{10}{25}=\dfrac{24}{60}=\dfrac{26}{65}=\dfrac{2}{5}$.

$\therefore$ Pilihan yang sesuai adalah $(B)\ 2:5$

27. Soal UN Matematika SMP 2015 |*Soal Lengkap

Perhatikan gambar di bawah ini!

Panjang $EF$ adalah...

$(A)\ 2\ \text{cm} $

$(B)\ 6\ \text{cm} $

$(C)\ 12\ \text{cm} $

$(D)\ 14\ \text{cm} $

Alternatif Pembahasan:

Bangun $ABCD$ jika kita beri variabel $x$ dan $y$ pada gambar, maka dapat seperti gambar berikut ini:

Dari gambar di atas dapat kita peroleh::
$\begin{align}
\dfrac{AE}{AD} & = \dfrac{x}{y} \\ \dfrac{2}{5} & = \dfrac{x}{15-10} \\ \dfrac{2}{5} & = \dfrac{x}{5} \\ x & = 2 \\ \hline EF & = 10+x =12 \end{align}$

Catatan!
Untuk menghitung panjang $EF$ seperti gambar dapat kita gunakan aturan:
$\begin{align}
EF & = \dfrac{AE \times DC + ED \times AB}{AE+ED} \\ EF & = \dfrac{2 \times 15 + 3 \times 10}{2+3} \\ & = \dfrac{30+30}{5}=12 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 12\ \text{cm}$

28. Soal UN Matematika SMP 2012 |*Soal Lengkap

Perhatikan gambar!

Segitiga $ABC$ kongruen dengan segitiga $POT$. Pasangan sudut yang sama besar adalah...

$(A)\ \angle BAC = \angle POT $

$(B)\ \angle BAC = \angle PTO $

$(C)\ \angle ABC = \angle POT $

$(D)\ \angle ABC = \angle PTO $

Alternatif Pembahasan:

Untuk melihat sisi-sisi yang sama pada bidang yang kongruen, dapat memperhatikan panjang sisi di depan sudut yang sama besar. Pada gambar di atas berlaku:

• sisi di depan $\angle C$ adalah $AB$, sisi di depan $\angle T$ adalah $OP$ dan $AB=OP$ maka $\angle C=\angle T$.
• sisi di depan $\angle B$ adalah $AC$, sisi di depan $\angle O$ adalah $PT$ dan $AC=PT$ maka $\angle B=\angle O$.
• sisi di depan $\angle A$ adalah $BC$, sisi di depan $\angle P$ adalah $OT$ dan $\angle A=\angle P$ maka $BC=TO$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ \angle ABC = \angle POT$

29. Soal UN Matematika SMP 2012 |*Soal Lengkap

Perhatikan gambar!

Jika $DE:DA=2:5$, maka panjang $EF$ adalah...

$(A)\ 10,4\ \text{cm} $

$(B)\ 36,4\ \text{cm} $

$(C)\ 64,4\ \text{cm} $

$(D)\ 69,4\ \text{cm} $

Alternatif Pembahasan:

Untuk menghitung panjang $EF$ seperti gambar dapat kita gunakan aturan:
$\begin{align}
EF & = \dfrac{DE \times AB + EA \times DC}{DE+EA} \\ EF & = \dfrac{2 \times 80 + 3 \times 54}{2+3} \\ EF & = \dfrac{160 + 162}{5} \\ & = \dfrac{322}{5}=64,4 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 64,4\ \text{cm}$

30. Soal UN Matematika SMP 2012 |*Soal Lengkap

Suatu tongkat yang panjangnya $2\ \text{m}$ mempunyai panjang bayangan $75\ \text{cm}$. Pada saat yang sama panjang bayangan sebuah menara TV $15\ \text{m}$. Tinggi menara TV tersebut adalah...

$(A)\ 40\ \text{m} $

$(B)\ 45\ \text{m} $

$(C)\ 48\ \text{m} $

$(D)\ 60\ \text{m} $

Alternatif Pembahasan:

Dengan menggunakan konsep perbandingan senilai maka kita peroleh:
$\begin{align}
\dfrac{t_{\text{tongkat}}}{t_{\text{menara}}} & = \dfrac{\text{bayangan}_{\text{tongkat}}}{\text{bayangan}_{\text{menara}}} \\ \dfrac{2\ \text{m}}{t_{\text{menara}}} & = \dfrac{75\ \text{cm}}{15\ \text{m}} \\ \dfrac{2\ \text{m}}{t_{\text{menara}}} & = \dfrac{0,75\ \text{m}}{15\ \text{m}} \\ t_{\text{menara}} \times 0,75\ \text{m} & = 2\ \text{m} \times 15\ \text{m} \\ t_{\text{menara}} & = \dfrac{30\ \text{m}^{2}}{0,75\ \text{m} } \\ & = 40\ \text{m} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 40\ \text{m}$

31. Soal UN Matematika SMP 2011 |*Soal Lengkap

Perhatikan gambar berikut!

Trapesium $ABCD$ sebangun dengan trapesium $EFGH$. Panjang $EH$ adalah...

$(A)\ 8\ \text{cm} $

$(B)\ 9\ \text{cm} $

$(C)\ 10\ \text{cm} $

$(D)\ 12\ \text{cm} $

Alternatif Pembahasan:

Trapesium $ABCD$ sebangun dengan trapesium $EFGH$, sehingga berlaku:
$\begin{align}
\dfrac{EH}{AD} & = \dfrac{FE}{AB} \\ \dfrac{EH}{8} & = \dfrac{18}{12} \\ EH & = \dfrac{18}{12} \times 8 \\ EH & = \dfrac{3}{2} \times 8 = 12 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 12\ \text{cm}$

32. Soal UN Matematika SMP 2011 |*Soal Lengkap

Perhatikan gambar!

Perbandingan sisi pada $\bigtriangleup ABC$ dan $\bigtriangleup ABD$ yang sebangun adalah...

$(A)\ \dfrac{AD}{AB}=\dfrac{BD}{BC}=\dfrac{AB}{AC} $

$(B)\ \dfrac{AD}{BD}=\dfrac{AB}{CD}=\dfrac{BD}{BC} $

$(C)\ \dfrac{AB}{BC}=\dfrac{AC}{BD}=\dfrac{BC}{CD} $

$(D)\ \dfrac{AB}{CD}=\dfrac{BC}{BD}=\dfrac{AC}{BC} $

Alternatif Pembahasan:

Dari informasi pada soal, jika kita gambarkan dapat seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Dari informasi sudut $\bigtriangleup ABC$ dan $\bigtriangleup ABD$ yang sebangun di atas dapat kita peroleh perbandingan sisi yang bersesuaian adalah sisi di depan sudut yang sama besar, $\dfrac{BC}{BD}=\dfrac{AB}{AD}=\dfrac{AC}{AB}$ atau $\dfrac{BD}{BC}=\dfrac{AD}{AB}=\dfrac{AB}{AC}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ \dfrac{AD}{AB}=\dfrac{BD}{BC}=\dfrac{AB}{AC}$

33. Soal UN Matematika SMP 2011 |*Soal Lengkap

Perhatikan gambar berikut!

Segitiga $ABC$ adalah segitiga siku-siku samakaki.
Jika $AB=10\ \text{cm}$ dan $CD$ garis bagi sudut $C$, panjang $BD$ adalah...

$(A)\ 5\ \text{cm} $

$(B)\ \left(10 \sqrt{2} - 10 \right)\ \text{cm} $

$(C)\ \left( 10 - 5 \sqrt{2} \right)\ \text{cm} $

$(D)\ \left( 5 \sqrt{2} - 5 \right)\ \text{cm} $

Alternatif Pembahasan:

Dari informasi pada soal, jika kita gambarkan dapat seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Dari gambar di atas kita peroleh $\bigtriangleup CBD$ dan $\bigtriangleup CED$ adalah kongruen.

Jika kita misalkan panjan $BD=x$ maka pada segitiga $AED$ kita peroleh:
$\begin{align}
AD^{2} &=AE^{2}+ED^{2} \\ \left( 10-x \right)^{2} &=\left( x \right)^{2}+\left( 10\sqrt{2}- 10 \right)^{2} \\ 100 -20x+x^{2} &= x^{2}+ 200 - 200\sqrt{2} + 100 \\ -20x &= 200 - 200\sqrt{2} \\ x &= -10 + 10\sqrt{2} \\ &= 10\sqrt{2} -10 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ \left(10 \sqrt{2} - 10 \right)\ \text{cm}$

34. Soal UN Matematika SMP 2010 |*Soal Lengkap

Perhatikan gambar berikut!

Titik $E$ dan $F$ adalah titik tengah $\overline{AC}$ dan $\overline{BD}$. Panjang $\overline{EF}$ adalah...

$(A)\ 3\ \text{cm} $

$(B)\ 4\ \text{cm} $

$(C)\ 6\ \text{cm} $

$(D)\ 8\ \text{cm} $

Alternatif Pembahasan:

Sebagai bantuan jika kita perpanjang garis $EF$, maka akan kita peroleh garis bantu seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Dari gambar di atas kita peroleh $\bigtriangleup AGE$ dan $\bigtriangleup ADC$ adalah sebangun, dimana $AE:AC=1:2$ sehingga dapat kita peroleh:
$\begin{align}
\dfrac{AE}{AC} &= \dfrac{GE}{DC} \\ \dfrac{1}{2} &= \dfrac{GE}{12} \\ GE &= 6 \end{align}$

Dari gambar di atas kita peroleh $\bigtriangleup DGF$ dan $\bigtriangleup DAB$ adalah sebangun, dimana $DF:DB=1:2$ sehingga dapat kita peroleh:
$\begin{align}
\dfrac{GF}{AB} &= \dfrac{DF}{DB} \\ \dfrac{GE+EF}{18} &= \dfrac{1}{2} \\ \dfrac{6+EF}{18} &= \dfrac{1}{2} \\ 6+EF &= 9 \\ EF &= 9-6=3 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 3\ \text{cm}$

35. Soal UN Matematika SMP 2010 |*Soal Lengkap

Sebuah foto berukuran $32\ \text{cm} \times 40\ \text{cm}$ dipasang pada sebuah bingkai. Lebar bingkai bagian kiri dan kanan $4\ \text{cm}$. Jika foto dan bingkai sebangun, sedangkan lebar bingkai bagian atas dan bawah sama, maka lebar bingkai bagian bawah adalah...

$(A)\ 4\ \text{cm} $

$(B)\ 5\ \text{cm} $

$(C)\ 8\ \text{cm} $

$(D)\ 10\ \text{cm} $

Alternatif Pembahasan:

Disampaikan pada soal lebar bingkai bagian kiri dan kanan $4\ \text{cm}$. Lebar bingkai bagian atas dan bawah belum diketahui, jika kita misalkan ukurannya dengan $x\ \text{cm}$ maka gambaran ukurannya dapat seperti berikut ini.

Foto dan bingkai sebangun, sehingga berlaku:
$\begin{align}
\dfrac{32}{40} & = \dfrac{40}{40+2x} \\ \dfrac{4}{5} & = \dfrac{40}{40+2x} \\ 4 \left( 40+2x \right) & = 5 \left( 40 \right) \\ 160+8x & = 200 \\ 8x & = 200-160 \\ 8x & = 40 \\ x & = 5 \end{align}$

Lebari bingkai bagian bawah adalah $x=5\ \text{cm}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 5\ \text{cm}$

36. Model Soal US-UM Matematika SMP |*Soal Lengkap

Perhatikan gambar!

Titik $E$ dan $F$ masing-masing pada $AD$ dan $BC$ sehingga $AE:ED=1:3$ dan $BF:FC=1:3$ maka panjang $EF=...\text{cm}$

$(A)\ 12 $

$(B)\ 13 $

$(C)\ 14 $

$(D)\ 15 $

Alternatif Pembahasan:

Dari informasi pada gambar, jika kita misalkan panjang $OD=x$ dan informasi lain kita tambahkan pada gambar dapat seperti berikut ini:

Dari gambar di atas, beberapa hal yang dapat kita simpulkan;

Dari informasi sudut pada gambar di atas, ada beberapa segitiga yang sebangun karena besar sudut yang bersesuaian sama besar. Sehingga kita peroleh:
$\begin{align}
\dfrac{DO}{AO} &=\dfrac{CD}{AB} \\
\dfrac{x}{AO} &=\dfrac{12}{24} \\
AO\ &=2x \\ \hline AD\ &=AO+OD \\ AD\ &=2x+x=3x \\ \hline AE\ &=\dfrac{1}{4}AD=\dfrac{1}{4}(3x)=\dfrac{3}{4}x \\ \hline ED\ &=\dfrac{3}{4}AD=\dfrac{3}{4}(3x)=\dfrac{9}{4}x \\ EO+OD\ &=\dfrac{9}{4}x \\ EO+x\ &=\dfrac{9}{4}x \\ EO\ &=\dfrac{5}{4}x \\ \end{align}$

Dari hasil di atas dan segitiga $OEF$ dan $OAB$ yang sebangun kita peroleh:
$\begin{align}
\dfrac{OE}{OA} &=\dfrac{EF}{AB} \\
\dfrac{\frac{5}{4}x}{2x} &=\dfrac{EF}{24} \\
\dfrac{5}{8} &=\dfrac{EF}{24} \\
EF &=\dfrac{5}{8} \times 24 \\
EF &=15 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 15$

37. Model Soal US-UM Matematika SMP |*Soal Lengkap

Dua baungun segitiga diaktakan kongruen apabila...

$(A)\ \text{Sisi yang bersesuaian tidak sama panjang}$

$(B)\ \text{Sudut-sudutnya kurag dari}\ 90^{\circ}$

$(C)\ \text{Sudut-sudut yang bersesuaian tidak sama besar}$

$(D)\ \text{Sudut-sudut yang bersesuaian sama besar}$

Alternatif Pembahasan:

Dua buah bangun dikatakan sebangun (kecuali lingkaran) apabila:

1. Besar sudut yang seletak atau bersesuaian sama besar.
2. Perbandingan panjang sisi yang seletak atau bersesuaian adalah sebanding.

Sebangun disimbolkan dengan $\sim$, misalkan $\bigtriangleup ABC$ sebangun dengan $\bigtriangleup PQR$ dapat dituliskan dengan $\bigtriangleup ABC \sim \bigtriangleup PQR$.

Karena $\angle A=\angle P$ dan $\angle B=\angle Q$ maka $\bigtriangleup ABC$ sebangun dengan $\bigtriangleup PQR$ dan dapat dituliskan $\bigtriangleup ABC \sim \bigtriangleup PQR$.

$\therefore$ Pilihan yang sesuai adalah $(D)\ \text{Sudut-sudut yang bersesuaian sama besar}$

38. Model Soal US-UM Matematika SMP |*Soal Lengkap

Sebuah foto berukuran tinggi $30\ \text{cm}$ dan lebar $20\ \text{cm}$ ditempel pada sebuah karton. Sisa karton di sebelah kiri, kanan, atas foto $2\ \text{cm}$. Jika foto dan karton sebangun, sisa karton di bawah foto adalah...

$(A)\ 5\ \text{cm} $

$(B)\ 4\ \text{cm} $

$(C)\ 3\ \text{cm} $

$(D)\ 2\ \text{cm} $

Alternatif Pembahasan:

Dari informasi pada soal dan kita misalkan sisa karton dibawah adalah $x$, jika kita gambarkan maka ilustrasinya dapat seperti berikut ini:

Foto dan karton sebangun, sehingga berlaku:
$\begin{align}
\dfrac{20}{30} & = \dfrac{24}{32+x} \\ \dfrac{2}{3} & = \dfrac{24}{32+x} \\ (2)(32+x) & = (3)(24) \\ 64+2x & = 72 \\ 2x & = 72-64 \\ 2x & = 8\ \longrightarrow x=4 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 4\ \text{cm}$

Catatan Pembahasan 30+ Soal Kesebangunan Dan Kekongruenan Matematika SMP di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.

JADIKAN HARI INI LUAR BIASA!
Ayo Share (Berbagi) Satu Hal Baik.

Keberhasilan bukanlah milik orang yang pintar, tapi milik orang yang tekun dan tidak pernah menyerah.

BJ Habibie