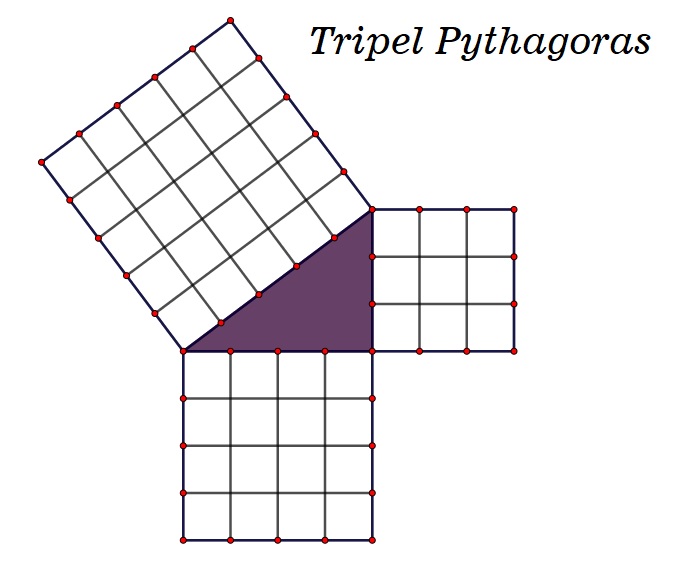
Pada artikel tulisan Bapak Prof.Hendra Gunawan yang berjudul Trypel Phytagoras disampaikan bahwa Tripel Pythagoras adalah tripel bilangan bulat positif $a,\ b,$ dan $c$ yang memenuhi persamaan $a^{2} + b^{2} = c^{2}$. Jika tertarik untuk menyimpan filenya silahkan 📥 Download File.
Contoh tripel Pythagoras yang paling sederhana adalah $3,\ 4,$ dan $5$, atau $5,\ 12,$ dan $13$, sebagaimana sering dibahas di SLTP. Pythagoras adalah seorang filsuf dan matematikawan Yunani kuno yang lahir sekitar tahun 580 SM.
Nama tripel Pythagoras diberikan karena Pythagoras, atau setidaknya para muridnya, diyakini sebagai orang yang pertama kali membuktikan bahwa persamaan $a^{2} + b^{2} = c^{2}$ sesungguhnya berlaku secara umum pada sembarang segitiga siku-siku dengan sisi-sisi tegak $a$ dan $b$ dan sisi miring $c$ (di sini $a,\ b,$ dan $c$ tidak harus merupakan bilangan bulat, tetapi sembarang bilangan real positif). Dalil ini pun kemudian dikenal sebagai Dalil Pythagoras.
Namun, sesungguhnya, tripel Pythagoras sudah dikenal oleh orang Babylonia sejak tahun 1600 SM. Pengetahuan tentang tripel Pythagoras diperlukan, misalnya, dalam tukar-menukar (barter) tanah pada zaman itu. Seseorang yang mempunyai sebidang tanah berukuran $50 \times 50$ meter kuadrat, misalnya, dapat menukarnya dengan dua bidang tanah berukuran $30 \times 30$ dan $40 \times 40$ meter kuadrat.
Pada zaman itu, orang Babylonia bahkan sudah tahu pula bagaimana menemukan tripel Pythagoras. Sebagai contoh, mereka tahu bahwa:
- Jika $m$ ganjil, maka $m,\ \frac{1}{2}(m^{2} - 1),$ dan $\frac{1}{2}(m^{2} + 1)$ merupakan tripel Pythagoras;
- Jika $m$ genap, maka $2m,\ (m^{2} - 1)$, dan $(m^{2} + 1)$ merupakan tripel Pythagoras.
Tetapi selain apa yang disampaikan diatas ada beberapa teorema Pythagoras yang tidak diajarkan pada sekolah biasa, dan mungkin, teorema ini juga yang mengakibatkan bahwa Pythagoras disebut seorang filsuf. Yang paling dikenal salah satunya adalah "Jika engkau tidak sanggup menahan lelahnya belajar, maka engkau harus menanggung pahitnya kebodohan".
Untuk menemukan bilangan tripel Pythagoras sudah disampaikan diatas, dengan bantuan microsoft exel mungkin kita akan dapat menemukan banyak bilangan tripel Pythagoras. Sehingga pada soal-soal trigonometri untuk SMA pada sisi-sisi segitiga siku-siku yang diketahui tidak semata-mata hanya menggunakan $3,\ 4,$ dan $5$, atau $5,\ 12,$ dan $13$.
Cara alternatif untuk anak SD atau SMP menemukan bilangan tripel Phytagoras dengan cara. Pilih dua bilangan asli $a$ dan $b$ dimana $ b \gt a$, lalu substitusi ke ($b^{2}-a^{2}$), ($2ab$), ($b^{2}+a^{2}$).
Misal kita pilih $5$ dan $6$ sehingga kita peroleh bilangan tripel phytagorasnya adalah ($6^{2}-5^{2}$), ($60$), ($6^{2}+5^{2}$) atau ($11,60,61$).
Berikut kita tampilkan 50 bilangan asli pertama dalam Tripel Pythagoras-nya.
$\begin{align}
(1):\ & - \\
(2):\ & - \\
(3):\ & (3,4,5) \\
(4):\ & (4,3,5) \\
(5):\ & (5,12,13) \\
(6):\ & (6,8,10) \\
(7):\ & (7,24,25) \\
(8):\ & (8,15,17) \\
(9):\ & (9,40,41) \\
(10):\ & (10,24,26) \\
(11):\ & (11,60,61) \\
(12):\ & (12,35,37) \\
(13):\ & (13,84,85) \\
(14):\ & (14,48,50) \\
(15):\ & (15,112,113) \\
(16):\ & (16,63,65) \\
(17):\ & (17,144,145) \\
(18):\ & (18,80,82) \\
(19):\ & (19,180,181) \\
(20):\ & (20,99,101) \\
(21):\ & (21,220,221) \\
(22):\ & (22,120,122) \\
(23):\ & (23,264,265) \\
(24):\ & (24,143,145) \\
(25):\ & (25,312,313) \\
(26):\ & (26,168,170) \\
(27):\ & (27,364,365) \\
(28):\ & (28,195,197) \\
(29):\ & (29,420,421) \\
(30):\ & (30,224,226) \\
(31):\ & (31,480,481) \\
(32):\ & (32,255,257) \\
(33):\ & (33,544,545) \\
(34):\ & (34,288,290) \\
(35):\ & (35,612,613) \\
(36):\ & (36,323,325) \\
(37):\ & (37,684,685) \\
(38):\ & (38,360,362) \\
(39):\ & (39,760,761) \\
(40):\ & (40,399,401) \\
(41):\ & (41,840,841) \\
(42):\ & (42,440,442) \\
(43):\ & (43,924,925) \\
(44):\ & (44,483,485) \\
(48):\ & (48,575,577) \\
(49):\ & (49,1200,1201) \\
(50):\ & (50,624,626)
\end{align}$
Bilangan tripel Pythagoras diatas tidak tunggal, bisa saja bilangan tersebut memiliki bilangan tripel Pythagoras dengan bentuk lain, misalnya untuk $48$, selain $(48,575,577)$ kita juga punya $(48,55,73)$.
Catatan tentang Contoh dan Cara Mudah Susun Bilangan Tripel Pythagoras di atas agar lebih baik lagi perlu catatan tambahan dari Anda. Untuk catatan tambahan atau hal lain yang perlu diketahui admin, silahkan disampaikan dan contact admin 🙏 CMIIW.
Ayo Share (Berbagi) Satu Hal Baik.
Jika engkau tidak sanggup menahan lelahnya belajar, Maka engkau harus menanggung pahitnya kebodohan.
