The good student, calon guru belajar matematika dasar lewat Rumus Trigonometri untuk Sudut Rangkap dan Sudut Pertengahan. Sudut rangkap atau sering juga disebut dengan sudut ganda. Catatan trigonometri ini akan membahas asal-usul rumus trigonomertri dan soal-soal latihan terkait sudut rangkap dan sudut pertengahan.
Pada catatan Rumus Jumlah dan Selisih Dua Sudut Perbandingan Trigonometri kita sudah dapat enam bentuk dasar rumus jumlah dan selisih dua sudut pada perbandingan trigonometri. Rumus jumlah dan selisih dua sudut pada trigonometri adalah:
- $ \sin \left ( A+B \right )=\sin A \cdot \cos B+\sin B \cdot \cos A $
- $ \sin \left ( A-B \right )=\sin A \cdot \cos B-\sin B \cdot \cos A $
- $ \cos \left ( A+B \right )=\cos A \cdot \cos B-\sin A \cdot \sin B $
- $ \cos\left ( A-B \right )=\cos A \cdot \cos B + \sin A \cdot \sin A $
- $ \tan \left ( A+B \right )=\dfrac{ \tan A+ \tan B}{1- \tan A\cdot \tan B} $
- $ \tan \left ( A-B \right )= \dfrac{ \tan A - \tan B}{1+ \tan A \cdot \tan B} $
Untuk rumus trigonometri sudut ganda atau sudut pertengahan adalah pengembangan dari rumus trigonometri di atas. Misalnya rumus sudut ganda $\sin 2A$ diperoleh dari penjabaran $\sin \left( A+A \right)$.
Sudut Rangkap (Ganda) Untuk Sinus
$\begin{align} \sin \left ( A+B \right ) &= \sin A \cdot \cos B+\sin B \cdot \cos A \\ \hline \sin \left ( A+A \right ) &= \sin A \cdot \cos A+\sin A \cdot \cos A \\ \sin 2A &= 2\sin A \cdot \cos A \\ \hline \sin \left ( 2A+2A \right ) &= \sin 2A \cdot \cos 2A+\sin 2A \cdot \cos 2A \\ \sin 4A &= 2\sin 2A \cdot \cos 2A \\ \hline & \vdots \end{align}$
Sudut Rangkap (Ganda) Untuk Cosinus
$\begin{align} \cos \left ( A+B \right ) &= \cos A \cdot \cos B-\sin A \cdot \sin B \\ \hline \cos \left ( A+A \right ) &= \cos A \cdot \cos A-\sin A \cdot \sin A \\ \cos 2A &= \cos^{2} A -\sin^{2} A \\ \hline \cos \left ( 2A+2A \right ) &= \cos 2A \cdot \cos 2A-\sin 2A \cdot \sin 2A \\ \cos 4A &= \cos^{2} 2A -\sin^{2} 2A \\ \hline & \vdots \end{align}$
Untuk sudut ganda cosinus, ada yang istimewa. Karena kita punya identitas trigonometri dasar yaitu $\sin^{2}A+\cos^{2}A=1$ yang dapat kita substitusi ke $\cos 2A$ atau $\cos 4A$.
$\begin{align}
\cos 2A &= \cos^{2} A -\sin^{2} A \\
\cos 2A &= \left( 1-\sin^{2} A \right) -\sin^{2} A \\
\cos 2A &= 1-2\sin^{2} A \\
\hline
\cos 2A &= \cos^{2} A -\sin^{2} A \\
\cos 2A &= \cos^{2} A - \left( 1-\cos^{2} A \right) \\
\cos 2A &= 2\cos^{2} A-1 \\
\hline
\cos 2A &= \cos^{2} A -\sin^{2} A \\
\cos 2A &= \left( \cos^{2} A -\sin^{2} A \right) \cdot \dfrac{\frac{1}{\cos^{2}A}}{\frac{1}{\cos^{2}A}} \\
\cos 2A &= \dfrac{\frac{\cos^{2} A -\sin^{2} A }{\cos^{2}A}}{\frac{1}{\cos^{2}A}} \\
\cos 2A &= \dfrac{\frac{\cos^{2} A -\sin^{2} A }{\cos^{2}A}}{\frac{\cos^{2} A +\sin^{2} A}{\cos^{2}A}} \\
\cos 2A &= \dfrac{1 -\tan^{2} A } {1 +\tan^{2} A }
\end{align}$
Bentuk di atas akan berlaku juga diterapkan untuk sudut ganda cosinus bentuk lain, misalnya $\cos 4A=1-2\sin^{2} 2A$ atau bentuk lainnya.
Sudut Rangkap (Ganda) Untuk Tangen
$\begin{align} \tan \left ( A+B \right ) &= \dfrac{ \tan A+ \tan B}{1- \tan A\cdot \tan B} \\ \hline \tan \left ( A+A \right ) &= \dfrac{ \tan A+ \tan A}{1- \tan A\cdot \tan A} \\ \tan 2A &= \dfrac{ 2 \tan A}{1- \tan^{2} A} \\ \hline \tan \left ( 2A+2A \right ) &= \dfrac{ \tan 2A+ \tan 2A}{1- \tan 2A\cdot \tan 2A} \\ \tan 4A &= \dfrac{ 2 \tan 2A}{1- \tan^{2} 2A} \\ \hline & \vdots \end{align}$
Sudut Pertengahan Untuk Sinus
Dari sudut ganda cosinus dapat juga kita kembangkan dan kita peroleh aturan untuk menghitung perbandingan trigonmetri sudut pertengahan.
$\begin{align}
\cos 2A &= 1-2\sin^{2} A \\
\hline
\text{misal}\ & A = \frac{1}{2}\alpha \\
\hline
\cos \left( 2 \cdot \frac{1}{2}\alpha \right) &= 1-2\sin^{2} \frac{1}{2}\alpha \\
\cos \alpha &= 1-2\sin^{2} \frac{1}{2}\alpha \\
2\sin^{2} \frac{1}{2}\alpha &= 1- \cos \alpha \\
\sin^{2} \frac{1}{2}\alpha &= \dfrac{1- \cos \alpha}{2} \\
\sin \frac{1}{2}\alpha &= \pm \sqrt{\dfrac{1- \cos \alpha}{2}}
\end{align}$
Tanda $ \pm$ digunakan tergantung kedudukan sudut misalnya $\sin 22\frac{1}{2}$ adalah $+$ dan $\sin 337\frac{1}{2}$ adalah $-$.
Sudut Pertengahan Untuk Cosinus
Dari sudut ganda cosinus dapat juga kita kembangkan dan kita peroleh aturan untuk menghitung perbandingan trigonmetri sudut pertengahan.
$\begin{align}
\cos 2A &= 2\cos^{2} A-1 \\
\hline
\text{misal}\ & A = \frac{1}{2}\alpha \\
\hline
\cos \left( 2 \cdot \frac{1}{2}\alpha \right) &= 2\cos^{2} \frac{1}{2}\alpha-1 \\
\cos \alpha &= 2\cos^{2} \frac{1}{2}\alpha-1 \\
2\cos^{2} \frac{1}{2}\alpha &= 1 + \cos \alpha \\
\cos^{2} \frac{1}{2}\alpha &= \dfrac{1+ \cos \alpha}{2} \\
\cos \frac{1}{2}\alpha &= \pm \sqrt{\dfrac{1 + \cos \alpha}{2}}
\end{align}$
Tanda $ \pm$ digunakan tergantung kedudukan sudut misalnya $\cos 22\frac{1}{2}$ adalah $+$ dan $\cos 157\frac{1}{2}$ adalah $-$.
Sudut Pertengahan Untuk Tangen
Untuk sudut pertengan untuk tangen dapat kita gunakan definisi $\tan A=\dfrac{\sin A}{\cos A}$, sehingga kita peroleh:
$\begin{align}
\tan \frac{1}{2}\alpha &=\dfrac{\sin \frac{1}{2}\alpha}{\cos \frac{1}{2}\alpha} \\
&= \dfrac{ \pm \sqrt{\dfrac{1 - \cos \alpha}{2}}}{ \pm\sqrt{\dfrac{1 + \cos \alpha}{2}}} \\
&= \pm \sqrt{ \dfrac{1 - \cos \alpha} {1 + \cos \alpha} } \\
\hline
\tan \frac{1}{2}\alpha &= \pm \sqrt{ \dfrac{1 - \cos \alpha} {1 + \cos \alpha} } \times \sqrt{ \dfrac{1 + \cos \alpha} {1 + \cos \alpha} } \\
&= \pm \sqrt{ \dfrac{1 - \cos^{2} \alpha} { \left(1 + \cos \alpha \right)^{2}}} \\
&= \pm \sqrt{ \dfrac{ \sin^{2} \alpha} { \left(1 + \cos \alpha \right)^{2}} } \\
&= \pm \dfrac{ \sin \alpha} { 1 + \cos \alpha } \\
\hline
\tan \frac{1}{2}\alpha &= \pm \sqrt{ \dfrac{1 - \cos \alpha} {1 + \cos \alpha} } \times \sqrt{ \dfrac{1 - \cos \alpha} {1 - \cos \alpha} } \\
&= \pm \sqrt{ \dfrac{ \left(1 - \cos \alpha \right)^{2} \alpha} { 1 - \cos^{2} \alpha}} \\
&= \pm \sqrt{ \dfrac{ \left(1 - \cos \alpha \right)^{2} } { \sin^{2} \alpha} } \\
&= \pm \dfrac{ 1 - \cos \alpha} { \sin \alpha }
\end{align}$
Tanda $ \pm$ digunakan tergantung kedudukan sudut.
Soal Latihan Sudut Rangkap (Ganda) dan Sudut Pertengahan
Soal trigonometri pada seleksi masuk perguruan tinggi negeri sangat sering diujikan. Berikut ini sebagai soal latihan kita pilih dari soal latihan pada Modul Matematika SMA Rumus Trigonometri Sudut Rangkap (Ganda) dan Sudut Pertengahan atau soal-soal yang ditanyakan pada media sosial.
Tunjukkan Kemampuan Matematika Terbaikmu!
| Nama Peserta : | |
| Tanggal Test : | |
| Jumlah Soal : | 13 soal |
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.
1. Soal Latihan Sudut Rangkap dan Pertengahan
Nilai dari $12 \cdot \sin 22\frac{1}{2}^{\circ} \cdot \cos 22\frac{1}{2}^{\circ} =\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\sin 2A = 2 \cdot \sin A \cdot \cos A$ dapat kita peroleh:
$\begin{align}
&\ 12 \cdot \sin 22\frac{1}{2}^{\circ} \cdot \cos 22\frac{1}{2}^{\circ} \\
&= 6 \cdot 2 \cdot \sin 22\frac{1}{2}^{\circ} \cdot \cos 22\frac{1}{2}^{\circ} \\
&= 6 \cdot \sin 2 \left( 22\frac{1}{2}^{\circ} \right) \\
&= 6 \cdot \sin 45^{\circ} \\
&= 6 \cdot \frac{1}{2}\sqrt{2} \\
&= 3\sqrt{2}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 3\sqrt{2}$
2. Soal Latihan Sudut Rangkap dan Pertengahan
Nilai dari $6-12 \cdot \sin^{2} \frac{\pi}{12} =\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\cos 2A = 1-2\sin^{2} A$ dapat kita peroleh:
$\begin{align}
&\ 6-12 \cdot \sin^{2} \frac{\pi}{12} \\
&= 6 \left( 1- 2 \cdot \sin^{2} \frac{\pi}{12} \right) \\
&= 6 \left( \cos 2 \cdot \frac{\pi}{12} \right) \\
&= 6 \left( \cos \frac{\pi}{6} \right) \\
&= 6 \left( \cos 30^{\circ} \right) \\
&= 6 \left( \dfrac{1}{2}\sqrt{3} \right) \\
&= 3\sqrt{3}
\end{align}$
Dengan menggunakan sifat $\sin \frac{1}{2}\alpha = \pm \sqrt{\dfrac{1- \cos \alpha}{2}} $ dapat kita peroleh:
$\begin{align}
&\ 6-12 \cdot \sin^{2} \frac{\pi}{12} \\
&= 6-12 \cdot \sin^{2} 15^{\circ} \\
&= 6-12 \cdot \left(\sin 15^{\circ} \right)^{2} \\
&= 6-12 \cdot \left( \sqrt{\dfrac{1- \cos 30^{\circ}}{2}} \right)^{2} \\
&= 6-12 \cdot \left( \dfrac{1- \frac{1}{2}\sqrt{3}}{2} \right) \\
&= 6-6 \cdot \left( 1- \frac{1}{2}\sqrt{3} \right) \\
&= 6-6+3\sqrt{3} \\
&= 3\sqrt{3}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 3\sqrt{3}$
3. Soal Latihan Sudut Rangkap dan Pertengahan
Nilai dari $4-8 \cdot \cos^{2} \frac{3\pi}{8} =\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\cos 2A = 2\cos^{2} A-1$ dapat kita peroleh:
$\begin{align}
&\ 4-8 \cdot \cos^{2} \frac{3\pi}{8} \\
&= -4 \left( -1+2 \cdot \cos^{2} \frac{3\pi}{8} \right) \\
&= -4 \left( 2 \cdot \cos^{2} \frac{3\pi}{8}-1 \right) \\
&= -4 \left( \cos 2 \cdot \frac{3\pi}{8} \right) \\
&= -4 \left( \cos \frac{3\pi}{4} \right) \\
&= -4 \left( \cos 135^{\circ} \right) \\
&= -4 \left( -\dfrac{1}{2}\sqrt{2} \right) \\
&= 2\sqrt{2}
\end{align}$
Dengan menggunakan sifat $\cos \frac{1}{2}\alpha = \pm \sqrt{\dfrac{1+ \cos \alpha}{2}} $ dapat kita peroleh:
$\begin{align}
&\ 4-8 \cdot \cos^{2} \frac{3\pi}{8} \\
&= 4-8 \cdot \cos^{2} 67\frac{1}{2}^{\circ} \\
&= 4-8 \cdot \left(\cos 67\frac{1}{2}^{\circ} \right)^{2} \\
&= 4-8 \cdot \left( \sqrt{\dfrac{1 + \cos 135^{\circ}}{2}} \right)^{2} \\
&= 4-8 \cdot \left( \dfrac{1- \frac{1}{2}\sqrt{2}}{2} \right) \\
&= 4-4 \cdot \left( 1- \frac{1}{2}\sqrt{2} \right) \\
&= 4-4 + 2\sqrt{2} \\
&= 2\sqrt{2}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(E)\ 2\sqrt{2}$
4. Soal Latihan Sudut Rangkap dan Pertengahan
Nilai dari $\dfrac{ 2 \cdot \tan 112,5^{\circ}}{1- \tan^{2} 112,5^{\circ}} =\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\tan 2A = \dfrac{ 2 \tan A}{1- \tan^{2} A}$ dapat kita peroleh:
$\begin{align}
\dfrac{ 2 \cdot \tan 112,5^{\circ}}{1- \tan^{2} 112,5^{\circ}}
&= \tan \left( 2 \cdot 112,5^{\circ} \right) \\
&= \tan 225^{\circ} \\
&= \tan \left( 180^{\circ} + 45^{\circ} \right) \\
&= \tan 45^{\circ} \\
&= 1
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 1$
5. Soal Latihan Sudut Rangkap dan Pertengahan
Jika $\sin A=\dfrac{1}{3}$ dan $A$ sudut lancip maka nilai $\cos 2A=\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\cos 2A = 1-2\sin^{2} A$ dapat kita peroleh:
$\begin{align}
\cos 2A
&= 1-2\sin^{2} A \\
&= 1 - 2 \left( \sin A \right)^{2} \\
&= 1 - 2 \left( \dfrac{1}{3}\right)^{2} \\
&= 1 - 2 \left( \dfrac{1}{9} \right)\\
&= 1 - \dfrac{2}{9} \\
&= \dfrac{7}{9}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ \dfrac{7}{9}$
6. Soal Latihan Sudut Rangkap dan Pertengahan
Jika $\tan \alpha=\dfrac{1}{2}$ dan $\alpha$ sudut lancip maka nilai $\sin 2\alpha=\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\sin 2A = 2\sin A \cdot \cos A$ dan bantuan segitiga siku-siku di bawah ini, dapat kita peroleh:
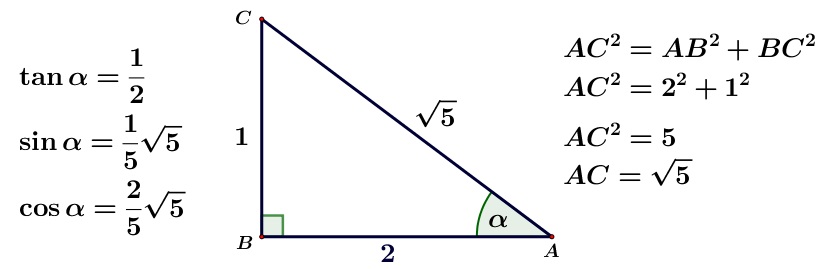
$\begin{align} \sin 2\alpha &= 2\sin \alpha \cdot \cos \alpha \\ &= 2 \cdot \dfrac{1}{5}\sqrt{5} \cdot \dfrac{2}{5}\sqrt{5} \\ &= \dfrac{4}{25} \cdot 5 \\ &= \dfrac{4}{5} \end{align}$
Jika tertarik untuk mengerjakan tanpa menggunakan bantuan segitiga siku-siku, dapat seperti berikut ini:
$\begin{align}
\tan \alpha & = \dfrac{1}{2} \\
\dfrac{\sin \alpha}{\cos \alpha} & = \dfrac{1x}{2x} \\
\hline
\sin^{2} \alpha + \cos^{2} \alpha &= 1 \\
\left( 1x \right)^{2} + \left( 2x \right)^{2} &= 1 \\
x^{2} + 4x^{2} &= 1 \\
5x^{2} &= 1 \longrightarrow x^{2}= \dfrac{1}{5} \\
\hline
\sin 2 \alpha &= 2\sin \alpha \cdot \cos \alpha \\
&= 2 \cdot \left( 1x \right) \cdot \left( 2x \right) \\
&= 4x^{2} \\
&= 4 \cdot \dfrac{1}{5} = \dfrac{4}{5}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ \dfrac{4}{5}$
7. Soal Latihan Sudut Rangkap dan Pertengahan
Jika $\sin A=\dfrac{3}{5}$ dan $A$ sudut tumpul maka nilai $\tan 2A=\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\tan 2A = \dfrac{ 2 \tan A}{1- \tan^{2} A}$ dan bantuan segitiga siku-siku di bawah ini, dapat kita peroleh:
$\begin{align} \tan 2\alpha &= \dfrac{ 2 \tan A}{1- \tan^{2} A} \\ &= \dfrac{ 2 \left( -\frac{3}{4} \right)}{1- \left( -\frac{3}{4} \right)^{2}} \\ &= \dfrac{ -\frac{3}{2}}{1- \frac{9}{16}} \\ &= \dfrac{ -\frac{3}{2}}{\frac{7}{16}}=\dfrac{ -24}{7} \\ \end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ -\dfrac{24}{7}$
8. Soal Latihan Sudut Rangkap dan Pertengahan
Jika $\tan B=\dfrac{1}{2}$ dan $B$ sudut pada kuadran III maka nilai $\cos 2B=\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\cos 2A = 2\cos^{2} A-1$ dan bantuan segitiga siku-siku di bawah ini, dapat kita peroleh:
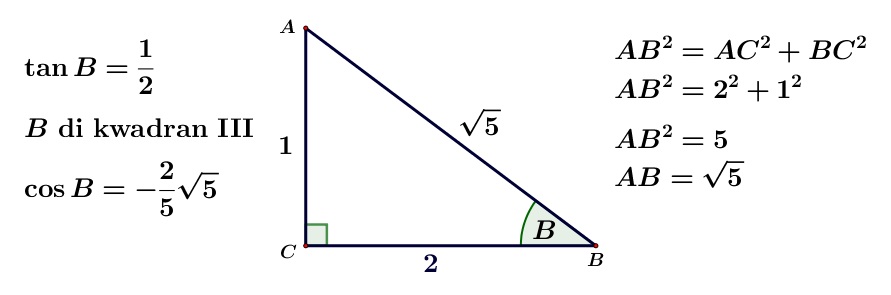
$\begin{align} \cos 2B &= 2\cos^{2} B-1 \\ &= 2 \left( -\dfrac{2}{5}\sqrt{5} \right)^{2} -1 \\ &= 2 \left( \dfrac{4}{5} \right)-1 \\ &= \dfrac{8}{5}-1 =\dfrac{3}{5} \end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ \dfrac{3}{5}$
9. Soal Latihan Sudut Rangkap dan Pertengahan
Nilai dari $\cos 72^{\circ}+\sin 72^{\circ} \cdot \tan 36^{\circ}=\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\sin 2A = 2 \sin A\ \cos A$ dan $\cos 2A = 1-2\sin^{2} A$ dapat kita peroleh:
$\begin{align}
&\ \cos 72^{\circ}+\sin 72^{\circ} \cdot \tan 36^{\circ} \\
&= \cos \left( 2 \cdot 36^{\circ} \right) +\sin \left( 2 \cdot 36^{\circ} \right) \cdot \tan 36^{\circ} \\
&= 1-2\sin^{2} 36^{\circ} + 2 \sin 36^{\circ} \cdot \cos 36^{\circ} \cdot \dfrac{\sin 36^{\circ}}{\cos 36^{\circ}} \\
&= 1-2\sin^{2} 36^{\circ} + 2 \sin^{2} 36^{\circ} \\
&= 1
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(E)\ 1$
10. Soal Latihan Sudut Rangkap dan Pertengahan
Bentuk $\dfrac{\sin 2A}{\sin A}-\dfrac{\cos 2A}{\cos A}$ sama dengan...
Alternatif Pembahasan:
Dengan menggunakan sifat $\sin 2A = 2 \sin A\ \cos A$ dan $\cos 2A = 2\cos^{2} A-1$ dapat kita peroleh:
$\begin{align}
&\ \dfrac{\sin 2A}{\sin A}-\dfrac{\cos 2A}{\cos A} \\
&= \dfrac{2 \sin A\ \cos A}{\sin A}-\dfrac{2\cos^{2} A-1}{\cos A} \\
&= 2 \cos A -\dfrac{2\cos^{2} A}{\cos A}+\dfrac{1}{\cos A} \\
&= 2 \cos A - 2\cos A + \sec A \\
&= \sec A
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ \sec A$
11. Soal Latihan Sudut Rangkap dan Pertengahan
Bentuk $\dfrac{\sin^{3}x+\cos^{3}x}{\sin x+\cos x}$ sama dengan...
Alternatif Pembahasan:
Dengan menggunakan sifat eksponen $a^{3}+b^{3}=\left(a+b\right)^{3}-3ab\left(a+b\right)$ dan beberapa identitas trigonometri dapat kita peroleh:
$\begin{align}
&\ \dfrac{\sin^{3}x+\cos^{3}x}{\sin x+\cos x} \\
&= \dfrac{\left( \sin x+\cos x \right)^{3}-3 \cdot \sin x \cos x \left( \sin x+\cos x \right)}{\sin x+\cos x} \\
&= \dfrac{\left( \sin x+\cos x \right)^{3}}{\sin x+\cos x} - \dfrac{3 \cdot \sin x \cos x \left( \sin x+\cos x \right)}{\sin x+\cos x} \\
&= \left( \sin x+\cos x \right)^{2} - 3 \cdot \sin x \cos x \\
&= \sin^{2} x+\cos^{2} x + 2 \cdot \sin x \cos x - 3 \cdot \sin x \cos x \\
&= 1 - \sin x \cos x \\
&= 1 - \frac{1}{2} \cdot \sin 2x
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 1 - \frac{1}{2} \cdot \sin 2x$
12. Soal Latihan Sudut Rangkap dan Pertengahan
$\cos 22\frac{1}{2}^{\circ}=\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\cos \frac{1}{2}\alpha = \pm \sqrt{\dfrac{1 + \cos \alpha}{2}}$ dan manipulasi aljabar dapat kita peroleh:
$\begin{align}
\cos 22\frac{1}{2} &= \cos \left( \frac{1}{2} \cdot 45^{\circ} \right) \\
&= \sqrt{\dfrac{1 + \cos 45^{\circ}}{2}} \\
&= \sqrt{\dfrac{1 + \frac{1}{2}\sqrt{2}}{2}} \\
&= \sqrt{\frac{1}{2} + \frac{1}{4}\sqrt{2}} \\
&= \sqrt{\frac{1}{4} \left( 2 + \sqrt{2} \right) } \\
&= \frac{1}{2} \sqrt{2 + \sqrt{2}}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ \dfrac{1}{2}\sqrt{2+\sqrt{2}}$
13. Soal Latihan Sudut Rangkap dan Pertengahan
$\sin 112\frac{1}{2}^{\circ}=\cdots$
Alternatif Pembahasan:
Dengan menggunakan sifat $\sin \frac{1}{2}\alpha = \pm \sqrt{\dfrac{1 - \cos \alpha}{2}}$ dan manipulasi aljabar dapat kita peroleh:
$\begin{align}
\sin 112\frac{1}{2}^{\circ} &= \sin \left( \frac{1}{2} \cdot 225^{\circ} \right)\\
&= \sqrt{\dfrac{1 - \cos 225^{\circ}}{2}} \\
&= \sqrt{\dfrac{1 - \cos \left( 180^{\circ}+45^{\circ} \right)}{2}} \\
&= \sqrt{\dfrac{1 + \cos 45^{\circ}}{2}} \\
&= \sqrt{\dfrac{1 + \frac{1}{2}\sqrt{2}}{2}} \\
&= \sqrt{\frac{1}{2} + \frac{1}{4}\sqrt{2}} \\
&= \sqrt{\frac{1}{4} \left( 2 + \sqrt{2} \right) } \\
&= \frac{1}{2} \sqrt{2 + \sqrt{2}}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ \frac{1}{2} \sqrt{2 + \sqrt{2}}$
Catatan Rumus Trigonometri Sudut Rangkap (Ganda) dan Sudut Pertengahan Dilengkapi Soal Latihan dan Pembahasan di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.
Ayo Share (Berbagi) Satu Hal Baik.
I have no special talent. I am only passionately curious. (Saya tidak memiliki bakat khusus. Hanya selalu menikmati rasa ingin tahu saja)
