Calon guru belajar matematika dasar SMP lewat soal dan pembahasan Bangun Ruang Sisi Datar (BRSD) dan Bangun Ruang Sisi Lengkung (BRSL) pada matematika SMP. Apa yang diharapkan setelah mempelajari materi ini, yaitu dengan aturan yang berlaku dan kreativitas berpikir kita dapat menyelesaikan masalah yang berkaitan dengan luas permukaan dan volume bangun ruang sisi datar (kubus, balok, prisma dan limas) dan bangun ruang sisi lengkung (tabung, kerucut, dan bola), serta gabungan beberapa bangun ruang.
Soal matematika dasar bangun ruang sisi datar atau bangun ruang sisi lengkung untuk SMP kita pilih dari soal-soal yang sudah pernah diujikan pada soal Ujian Sekolah matematika SMP, soal Ujian Nasional matematika SMP, atau soal ujian seleksi akademik masuk SMA Unggulan atau SMA Plus.
BANGUN RUANG SISI DATAR (BRSD)
Bangun ruang yang dikategorikan dengan bangun ruang sisi datar adalah kubus, balok, prisma dan limas.
KUBUS
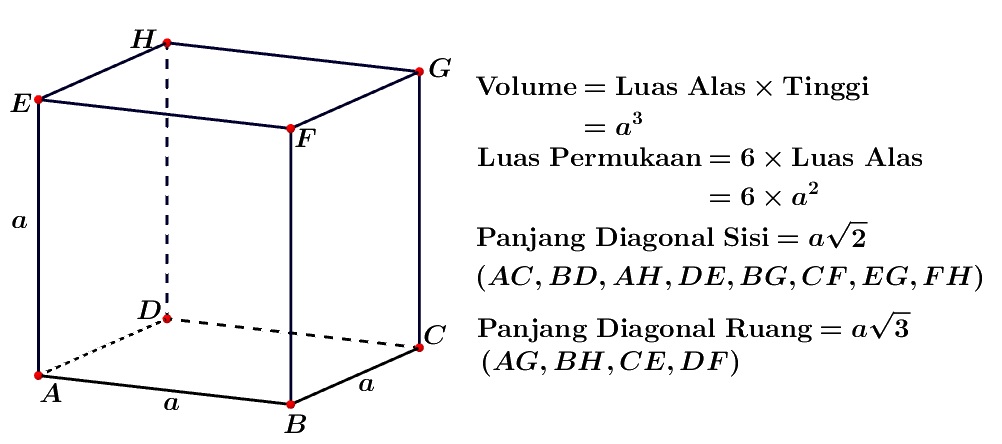
BALOK
PRISMA
LIMAS
BANGUN RUANG SISI LENGKUNG (BRSL)
Bangun ruang yang dikategorikan dengan bangun ruang sisi lengkun adalah tabung, kerucut dan bola.
TABUNG
KERUCUT
BOLA
Pembahasan Soal Bangun Ruang Sisi Datar dan Sisi Lengkung Matematika SMP
Untuk menambah pemahaman kita terkait Bangun Ruang Sisi Datar dan Sisi Lengkung, mari kita simak beberapa soal latihan di bawah ini. Soal latihan kita pilih dari soal-soal yang diujikan pada Ujian Nasional matematika SMP atau Ujian Sekolah matematika SMP.
Catatan matematika SMP tentang soal dan pembahasan Bangun Ruang Sisi Datar dan Sisi Lengkung ini kita bagi menjadi dua catatan, agar dapat dicoba dan dipelajari secara optimal.
Soal latihan Bangun Ruang Sisi Datar dan Sisi Lengkung berikut ini, silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan Periksa Jawaban dan jika hasilnya belum memuaskan, pilih Ulangi Tes untuk tes ulang.
Tunjukkan Kemampuan Terbaikmu!
| Nama Peserta : | |
| Tanggal Tes : | |
| Jumlah Soal : | 40 soal |
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.
1. Soal UNBK Matematika SMP 2019 |*Soal Lengkap
Perhatikan balok berikut!
Panjang diagonal ruang $DF$ adalah...
Alternatif Pembahasan:
Panjang diagonal ruang $DF$ pada balok $ABCD.EFGH$ adalah
$\begin{align}
DF^{2} &= AB^{2}+BC^{2}+AE^{2} \\
&= 36^{2}+16^{2}+12^{2} \\
&= 1296+256+144 \\
&= 1696 \\
DF &= \sqrt{1696}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ \sqrt{1696}$
2. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap
Perhatikan gambar!
Catar memiliki kawat panjangnya $2,5$ meter yang akan dibuat kerangka bangun seperti di atas. Panjang kawat yang tidak terpakai adalah...
Alternatif Pembahasan:
Pada gambar terdapat empat rangka bangun ruang yang akan dibuat Catar, yaitu kubus, balok, limas persegi beraturan dan prisma.
- Kawat yang diperlukan untuk membuat rangka kubus adalah $6\ \text{cm} \times 12 = 72\ \text{cm}$
- Kawat yang diperlukan untuk membuat rangka balok adalah $8\ \text{cm} \times 4 + 5\ \text{cm} \times 4 + 2\ \text{cm} \times 4$$=32\ \text{cm}+ 20\ \text{cm} + 8\ \text{cm}$$=60\ cm$
- Kawat yang diperlukan untuk membuat rangka limas adalah $8\ \text{cm} \times 4 + 10\ \text{cm} \times 4$$=32\ \text{cm}+ 40\ \text{cm}$$=72\ \text{cm}$
- Kawat yang diperlukan untuk membuat rangka prisma adalah $3\ \text{cm} \times 6 + 5\ \text{cm} \times 3$$=18\ \text{cm}+ 15\ \text{cm}$$=33\ \text{cm}$
Kawat yang tersedia adalah $2,5\ \text{m}=250\ \text{cm}$ maka sisa kawat $250 - 237=13\ \text{cm}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 13\ \text{cm}$
3. Soal UNBK Matematika SMP 2018 |*Soal Lengkap
Diketahui prisma dengan banyak rusuk dan sisi berturut-turut $18$ dan $8$. Alas prisma tersebut berbentuk...
Alternatif Pembahasan:
Banyak rusuk adalah $18$ dan banyak sisi adalah $8$.
Kita coba analisis dari banyak sisi, karena prisma sisi atas dan sisi alas sama maka sisi samping tinggal $6$.
Karena sisi samping adalah $6$, maka alasnya berbentuk segienam.
Ini juga sesuai dengan banyak rusuk $18$ yang terdiri dari rusuk alas $6$, rusuk atas $6$ dan rusuk samping $6$.
$\therefore$ Alas prisma tersebut berbentuk $(A)\ \text{segienam}$
4. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap
Perhatikan bangun prisma trapesium siku-siku berikut!
Luas permukaan bangun adalah...
Alternatif Pembahasan:
Untuk menghitung luas permukaan prisma, kita akan menghitung luas keenam bangun yang membentuk prisma tersebut yaitu $[ABFE]$, $[DCGH]$, $[BCGF]$, $[BCGF]$, $[EFGH]$, dan $[ABCD]$. Tetapi ada bagian prisma yang belum diketahui panjangnya yaitu $AE$.
Jika kita ambil titik $F'$ pada $AB$ sehingga $AE // FF'$ dan $AE = FF'$, maka dapat kita terapkan teorema pythagoras pada segitiga $BFF'$;
$ \begin{align}
FF'^{2} &= BF^{2}-BF'^{2} \\
FF'^{2} &= 17^{2}-8^{2} \\
FF' &= \sqrt{289-64} \\
FF' &= \sqrt{225}=15
\end{align} $
Luas permukaan prisma;
$ \begin{align}
L & =2 \times [ABFE]+ [ADHE]+[BCGF]+[EFGH]+[ABCD] \\
& = 2 \times \left[ \frac{1}{2} (12+20) \times 15 \right] + [15 \times 15]+[15 \times 17]+[12 \times 15]+ [15 \times 20] \\
& = 32 \times 15+ 225+255+180+300 \\
& = 480+225+255+180+ 300 \\
& = 1440
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(D)\ 1.440\ \text{cm}^{2}$
5. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap
Perhatikan gambar kubus berikut!
Bidang diagonal yang tegak lurus dengan $BCHE$ adalah...
Alternatif Pembahasan:
Bidang diagonal yang tegak lurus dengan $BCHE$ adalah $ADGF$, seperti tampak pada gambar berikut ini.
$\therefore$ Pilihan yang sesuai adalah $(B)\ \text{bidang}\ ADGF $
6. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2009 |*Soal Lengkap
Kolam renang Pagar Beton dirancang dengan bentuk sebagai berikut:
Volum air di dalam kolam adalah...
Alternatif Pembahasan:
Untuk menghitung volume kolam renang seperti gambar, dapat kita hitung menjadi tiga bagian:
- Bagian I: Balok dengan ukuran $p=10,\ l=15,\ t=1,5$ ;
$V=10 \times 15 \times 1,5 =225$ - Bagian II: Balok dengan ukuran $p=5,\ l=15,\ t=2,5$ ;
$V=5 \times 15 \times 2,5 =187.5$ - Bagian III: Balok dengan ukuran $p=15,\ l=15,\ t=4$ ;
$V=15 \times 15 \times 4 =900$ - Volume total adalah $225+187,5+900=1312,5$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 1312,5\ m^{3}$
7. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2007 |*Soal Lengkap
Kolam renang berukuran panjang $50\ m$ dan lebar $16\ m$. Kedalaman air pada ujung yang dangkal $1\ m$ terus melandai hingga pada ujungnya yang dalam $3\ m$ seperti tampak pada gambar di bawah ini...
Volume air di dalam kolam adalah...
Alternatif Pembahasan:
Jika kita perhatikan gambar, kolam berbentuk seperti sebuah prisma sehingga volume bisa kita hitung dengan luas alas kali tinggi, dimana tingginya sudah diketahui yaitu $16\ m$.
Luas alas berupa segiempat $(1\ m \times 50\ m)$ dan segitiga $(\dfrac{1}{2} \times 50\ m \times 2\ m)$. Sehingga luas alas total adalah $50\ m^{2} + 50\ m^{2} =100\ m^{2}$.
Volume kolam adalah $100\ m^{2} \times 16\ m =1600\ m^{3}$.
$\therefore$ Pilihan yang sesuai adalah $(B)\ 1600\ m^{3}$
8. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2007 |*Soal Lengkap
Empat macam rangkaian enam bujur sangkar di atas, yang merupakan jaring-jaring kubus adalah...
Alternatif Pembahasan:
Jika dicoba merangkai jaring-jaring di atas menjadi sebuah kubus yang memungkinkan adalah jaring-jaring nomor $(1)$ dan $(3)$.
$\therefore$ Pilihan yang sesuai adalah $(B)\ (1)\ \text{dan}\ (3)$
9. Soal UN Matematika SMP 2011 |*Soal Lengkap
Indra akan membuat tiga buah papan nama dari kertas karton yang bagian kiri dan kananya terbuka seperti tampak pada gambar. Luas minimum karton yang diperlukan Indra adalah...
Alternatif Pembahasan:
Berdasarkan informasi dari soal dan pada gambar, papan nama yang akan dibuat seperti prisma segitiga dimana alas dan atasnya tidak ada. Sehingga untuk menghitung banyak karton yang digunakan kita hitung dari luas permukaan prisma segitiga tanpa alas dan atas.
Banyak karton yang diperlukan adalah:
$ \begin{align}
L & =3 \times \left( 22 \times 5 + 22 \times 12 + 22 \times 13 \right) \\
& =3 \times \left( 110 + 264 + 286 \right) \\
& =3 \times \left( 660 \right) \\
& = 1.980
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(C)\ 1.980\ \text{cm}^{2}$
10. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2005 |*Soal Lengkap
Gambar di samping merupakan jaring-jaring...
Alternatif Pembahasan:
Dari gambar yang ditampilkan di atas, jaring-jaring merupakan jaring-jaring prisma, tepatnya prisma segitiga
$\therefore$ Pilihan yang sesuai adalah $(B)\ \text{Prisma}$
11. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2004 |*Soal Lengkap
Kubus yang panjang seluruh rusuknya $72$ cm mempunyai luas permukaan adalah...
Alternatif Pembahasan:
Kubus mempunyai rusuk yang sama sebanyak $12$ buah, sehingga saat panjang seluruh rusuknya $72$ cm maka panjang salah satu rusuknya adalah $\dfrac{72}{12}=6$.
Luas permukaan kubus terdiri dari $6$ persegi yang kongruen dimana panjang rusuknya adalah $6$, maka luas seluruh permukaan kubus adalah $6 \times 6 \times 6=216\ cm^{2}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 216\ \text{cm}^{2}$
12. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2004 |*Soal Lengkap
Limas $T.ABCD$ diketahui panjang rusuk-rusuknya sama. Perbandingan luas alas $ABCD$ dengan luas seluruh sisi tegaknya adalah...
Alternatif Pembahasan:
Panjang rusuk limas $T.ABCD$ adalah sama maka limas dibentuk oleh $4$ segitiga samasisi dan sebuah persegi.
Kita misalkan panjang rusuk adalah $a$, maka Perbandingan luas alas $ABCD$ dengan luas seluruh sisi tegaknya adalah
$\begin{align}
\dfrac{[ABCD]}{4[TAB]} & = \dfrac{a^{2}}{4 \times \frac{1}{4} a^{2} \sqrt{3} } \\
\dfrac{[ABCD]}{4[TAB]} & = \dfrac{a^{2}}{a^{2} \sqrt{3} } \\
\dfrac{[ABCD]}{4[TAB]} & = \dfrac{1}{\sqrt{3} } \\
\dfrac{[ABCD]}{4[TAB]} & = \dfrac{1}{\sqrt{3} }
\end{align}$
Menghitung $[TAB]$
$\begin{align}
t & = \sqrt{a^{2}-\left(\frac{1}{2}a \right)^{2}} \\
& = \sqrt{a^{2}-\frac{1}{4}a^{2}} \\
& = \sqrt{\frac{3}{4}a^{2}} \\
& = \frac{1}{2} a \sqrt{3} \\
[TAB] & = \frac{1}{2} AB \times t \\
& = \frac{1}{2} a \times \frac{1}{2} a \sqrt{3} \\
& = \frac{1}{4} a^{2} \sqrt{3} \\
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 1:\sqrt{3}$
13. Soal UN Matematika SMP 2010 |*Soal Lengkap
$ABCD.EFGH$ pada gambar di bawah ini adalah prisma dengan $ABFE$ sejajar $DCGH$. Panjang $AB=4\ \text{cm}$, $BC=6\ \text{cm}$, $AE=8\ \text{cm}$, dan $BF=5\ \text{cm}$. Luas permukaan prisma adalah...
Alternatif Pembahasan:
Untuk menghitung luas permukaan prisma, kita akan menghitung luas keenam bangun yang membentuk prisma tersebut.
Luas permukaan prisma;
$ \begin{align}
L & =2 \times \left[ \frac{1}{2} (AE+BF) \times AB \right] + [AB \times BC]+[BC \times BF]+[AD \times AE]+ [EF \times FG] \\
& = 2 \times \left[ \frac{1}{2} (8+5) \times 4 \right] + [4 \times 6]+[6 \times 5]+[6 \times 8]+ [5 \times 6] \\
& = \left[ (13) \times 4 \right] + 54 + 78 \\
& =52 + 132 \\
& = 184
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(C)\ 184\ \text{cm}^{2}$
14. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2004 |*Soal Lengkap
Kubus merupakan suatu bangun yang dapat disebut juga sebagai...
Alternatif Pembahasan:
Kubus merupakan suatu bangun yang dapat disebut juga sebagai prisma yaitu prisma segiempat beraturan, karena prisma adalah dimana bagian alasnya sama dengan baian atasnya. Begitu juga dengan tabung dapat juga disebut sebagai prisma.
$\therefore$ Pilihan yang sesuai adalah $(D)\ \text{prisma}$
15. Soal UN Matematika SMP 2018 |*Soal Lengkap
Suatu prisma memiliki $36$ buah rusuk dan $14$ sisi. Bentuk alas prisma tersebut adalah...
Alternatif Pembahasan:
Berdasarkan informasi pada soal, prisma memiliki $36$ buah rusuk dan $14$ sisi.
Prisma memiliki alas dan atasnya sama, maka dari $14$ sisi ini dua sisi diantaranya merupakan alas dan atas, sehingga sisi tegak prisma adalah $12$ sisi. Karena sisi tegak prisma ada $12$ sisi maka alas prisma adalah segi dua belas.
$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{segi dua belas}$
16. Soal UN Matematika SMP 2018 |*Soal Lengkap
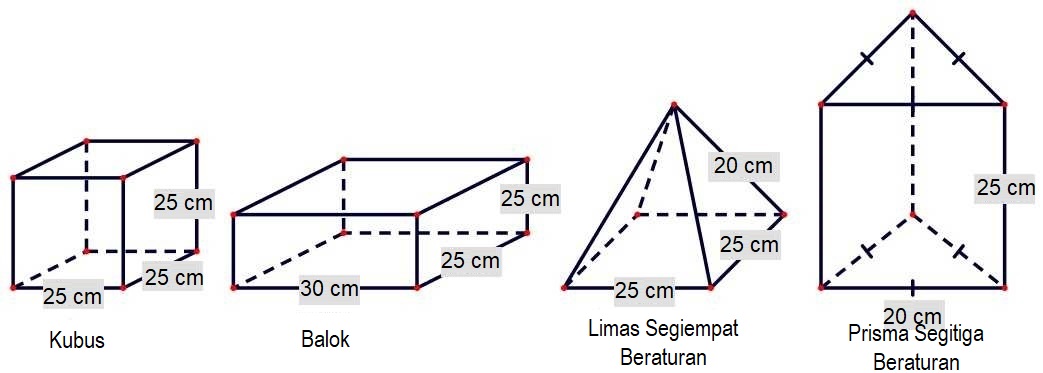
Pak Budi memiliki kawat panjangnya $10\ m$ yang akan dibuat empat kerangka bangun ruang seperti gambar berikut.
Sisa kawat yang dimiliki Pak Budi adalah...
Alternatif Pembahasan:
Pada gambar terdapat empat rangka bangun ruang yang akan dibuat pak Budi, yaitu kubus, balok, limas segiempat beraturan dan prisma segitiga.
- Kawat yang diperlukan untuk membuat rangka kubus adalah $25\ \text{cm} \times 12 = 300\ \text{cm}$ atau $3\ m$
- Kawat yang diperlukan untuk membuat rangka balok adalah $30\ \text{cm} \times 4 + 25\ \text{cm} \times 8=120\ \text{cm}+ 200\ \text{cm}$ atau $3,2\ \text{m}$
- Kawat yang diperlukan untuk membuat rangka limas adalah $25\ \text{cm} \times 4 + 20\ \text{cm} \times 4=100\ \text{cm}+ 80\ \text{cm}$ atau $1,8\ \text{m}$
- Kawat yang diperlukan untuk membuat rangka prisma adalah $20\ \text{cm} \times 6 + 25\ \text{cm} \times 3=120\ \text{cm}+ 75\ \text{cm}$ atau $1,95\ \text{m}$
Total kawat yang dibutuhkan untuk membuat rangka bangun adalah $3+3,2+1,8+1,95=9,95\ \text{m}$.
Kawat yang tersedia adalah $10\ \text{m}$ maka sisa kawat $10\ \text{m} - 9,95\ \text{m}=0,05\ \text{m}$ atau $5\ \text{cm}$.
$\therefore$ Pilihan yang sesuai adalah $(A)\ 5\ cm$
17. Soal UN Matematika SMP 2017 |*Soal Lengkap
Gambar di samping adalah mainan anak-anak yang berbentuk balok, tersusun dari kubus-kubus satuan yang kongruen. Jika seluruh permukaan balok tersebut dicat, banyaknya kubus satuan yang terkena cat pada dua sisinya saja ada...
Alternatif Pembahasan:
Dari kondisi balok yang disusun dari beberapa kubus seperti gambar, jika dicat maka sisi kubus yang terkena cat tepat pada dua sisi kubus adalah kubus yang berada diantara kubus yang tepat disudut.
- Pada sisi atas balok, kubus yang terkena cat dua sisi ada sebanyak $3 \times 4 =12$ kubus.
- Pada sisi samping balok, kubus yang terkena cat dua sisi ada sebanyak $1 \times 4 =4$ kubus.
- Pada sisi bawah balok, kubus yang terkena cat dua sisi ada sebanyak $3 \times 4 =12$ kubus.
- Total kubus yang terkena cat dua sisi adalah $12+4+12=28$ kubus.
$\therefore$ Pilihan yang sesuai adalah $(D)\ 28\ cm$
18. Soal UN Matematika SMP 2017 |*Soal Lengkap
Sebuah kerangka akuarium berbentuk prisma dengan alas berbentuk trapesium samakaki tampak seperti gambar di samping ini. Kerangka tersebut terbuat dari aluminium dengan harga tiap meter $\text{Rp}25.000,00$. Biaya minimal untuk pembelian seluruh aluminium adalah...
Alternatif Pembahasan:
Untuk mendapatkan banyak alumuminium yang dibutuhkan membuat kerangka akuarium, kita perlu menghitung keliling dari sisi-sisi akuarium yaitu:
- Rangka sisi alas dan atas akuarium, $2 \times \left( 1,4+0,8+0,6+0,8 \right)=7,2$.
- Rangka sisi tegak akuarium, $4 \times \left( 0,6 \right)=2,4$.
- Total aluminium yang dibutuhkan adalah $2,4+7,2=9,6$ sehingga uang yang diperlukan adalah $9,6 \times \text{Rp}25.000,00$ yaitu $\text{Rp}240.000,00$.
$\therefore$ Pilihan yang sesuai adalah $(D)\ \text{Rp}240.000,00$
19. Soal UN Matematika SMP 2017 |*Soal Lengkap
Sebuah prisma alasnya berbentuk jajargenjang dengan panjang alas $15\ \text{cm}$ dan tinggi $8\ \text{cm}$. Jika tinggi prisma $20\ \text{cm}$, volume prisma tersebut adalah...
Alternatif Pembahasan:
Volume prisma adalah $\text{luas alas} \times \text{tinggi}$, untuk alas berupa jajargenjang maka volume prisma adalah:
$\begin{align}
V\ &= L_{\text{jajargenjang}} \times \text{tinggi} \\
&= 15\ \text{cm} \times 8\ \text{cm} \times 20\ \text{cm} \\
&= 120\ \text{cm}^{2} \times 20\ \text{cm} \\
&= 2.400\ \text{cm}^{3}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 2.400\ \text{cm}^{3}$
20. Soal UN Matematika SMP 2016 |*Soal Lengkap
Perhatikan gambar kubus berikut!
Bidang diagonal yang tegak lurus dengan $ABGH$ adalah...
Alternatif Pembahasan:
Bidang diagonal yang tegak lurus dengan $ABGH$ adalah $CDEF$, seperti tampak pada gambar berikut ini.
$\therefore$ Pilihan yang sesuai adalah $(C)\ CDEF $
21. Soal UN Matematika SMP 2016 |*Soal Lengkap
Akmal membuat sebuah kerangka berbentuk balok yang terbuat dari aluminum dengan ukuran $50\ \text{cm} \times 50\ \text{cm} \times 80\ \text{cm}$. Jika harga $1\ \text{m}$ aluminimum $\text{Rp}4.000,00$, biaya yang diperlukan untuk membeli aluminium adalah...
Alternatif Pembahasan:
Untuk mendapatkan banyak alumuminium yang dibutuhkan membuat kerangka akuarium, kita perlu menghitung keliling dari rangka akuarium. Kerangka akuarium berbentuk balok dengan ukuran $50\ \text{cm} \times 50\ \text{cm} \times 80\ \text{cm}$ yang kita anggap $p=50\ \text{cm}$, $l=50\ \text{cm}$, dan $t=80\ \text{cm}$ maka dapat kita peroleh:
- Rangka sisi alas dan atas akuarium, $2 \times \left( 4 \times 50 \text{cm} \right)=400\ \text{cm}$.
- Rangka sisi tegak akuarium, $4 \times \left( 80\ \text{cm} \right)=320\ \text{cm}$.
- Total aluminium yang dibutuhkan adalah $400\ \text{cm}+320\ \text{cm}=720\ \text{cm}$ atau $7,2\ \text{m}$ sehingga uang yang diperlukan paling sedikit adalah $7,2 \times \text{Rp}4.000,00$ yaitu $\text{Rp}28.800,00$.
$\therefore$ Pilihan yang sesuai adalah $(D)\ \text{Rp}28.800,00$
22. Soal UNBK Matematika SMP 2019 |*Soal Lengkap
Limas dengan alas persegi mempunyai tinggi $8\ \text{cm}$ dan keliling alas $60\ \text{cm}$, Volume limas tersebut adalah...
Alternatif Pembahasan:
Volume limas adalah $\dfrac{1}{3}$
times \text{Luas Alas} \times Tinggi$
Karena alas limas sebuah persegi dengan keliling $60\ \text{cm}$, panjang sisinya adalah $\dfrac{60\ \text{cm}}{4}=15\ \text{cm}$ dan luasnya adalah $\left( 15\ \text{cm} \right)^{2}=225\ \text{cm}^{2}$.
Volume limas adalah:
$\begin{align}
V &= \dfrac{1}{3} times \text{Luas Alas} \times \text{Tinggi} \\
&= \dfrac{1}{3} times 225\ \text{cm}^{2} \times 8\ \text{cm} \\
&= \dfrac{1}{3} times 1800\ \text{cm}^{3} \\
&= 600\ \text{cm}^{3}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 600$
23. Soal UN Matematika SMP 2016 |*Soal Lengkap
Perhatikan gambar prisma trapesium siku-siku berikut!
Luas permukaan bangun adalah...
Alternatif Pembahasan:
Untuk menghitung luas permukaan prisma, kita akan menghitung luas keenam bangun yang membentuk prisma tersebut. Tetapi ada bagian prisma yang belum diketahui panjangnya yaitu "sisi miring".
Untuk menghitung "sisi miring" yang belum diketahui di atas dapat kita gunakan teorema pythagoras, yaitu:
$ \begin{align}
\sqrt{6^{2}+8^{2}} &= \sqrt{36+64} \\
&= \sqrt{100} =10
\end{align} $
Luas permukaan prisma;
$ \begin{align}
L & =2 \times \left[ \frac{1}{2} (16+10) \times 8 \right] + [20 \times 8]+[20 \times 10]+[20 \times 10]+ [20 \times 16] \\
& = 26 \times 8+ 160+200+200+320 \\
& = 208+160+200+200+320 \\
& = 1.088
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(C)\ 1.088\ \text{cm}^{2}$
24. Soal UN Matematika SMP 2016 |*Soal Lengkap
Banyak diagonal ruang balok adalah...
Alternatif Pembahasan:
Banyak diagonal ruang balok adalah sebanyak $4$ buah, silahkan perhatikan gambar diagonal ruang pada balok di bawah ini.
$\therefore$ Pilihan yang sesuai adalah $(C)\ 8$
25. Soal UN Matematika SMP 2015 |*Soal Lengkap
Anita ingin membuat kerangka limas persegi dengan panjang rusuk alas $30\ \text{cm}$ dan panjang rusuk tegaknya $24\ \text{cm}$. Jika Anita memiliki kawat sepanjang $10\ \text{meter}$, maka kerangka limas yang dapat dibuat adalah...
Alternatif Pembahasan:
Untuk membuat sebuah kerangka limas dengan rusuk alas $30\ \text{cm}$ dan rusuk tegak $24\ \text{cm}$ adalah:
$\begin{align}
K_{\text{limas}} &= K_{\text{alas}}+K_{\text{tegak}} \\
&= 4 \times 30\ \text{cm}+ 4 \times 24\ \text{cm} \\
&= 120\ \text{cm} + 96\ \text{cm} \\
&= 216\ \text{cm} = 2,16\ \text{m}
\end{align}$
Banyak rangka limas yang dapat dibuat adalah $\dfrac{10}{2,16}=4,6...$, sehingga banyak rangka limas yang dapat dibuat paling banyak adalah $4$.
$\therefore$ Pilihan yang sesuai adalah $(A)\ 4$
26. Soal UN Matematika SMP 2015 |*Soal Lengkap
Sebuah prisma tegak, alas berbentuk belahketupat dengan panjang diagonal $12\ \text{cm}$ dan $16\ \text{cm}$. Jika tinggi prisma $25\ \text{cm}$, maka luas permukaan prisma adalah...
Alternatif Pembahasan:
Untuk menghitung luas permukaan prisma, kita akan menghitung luas keenam bangun yang membentuk prisma tersebut. Tetapi ada bagian prisma yang belum diketahui panjang "sisi belahketupat".
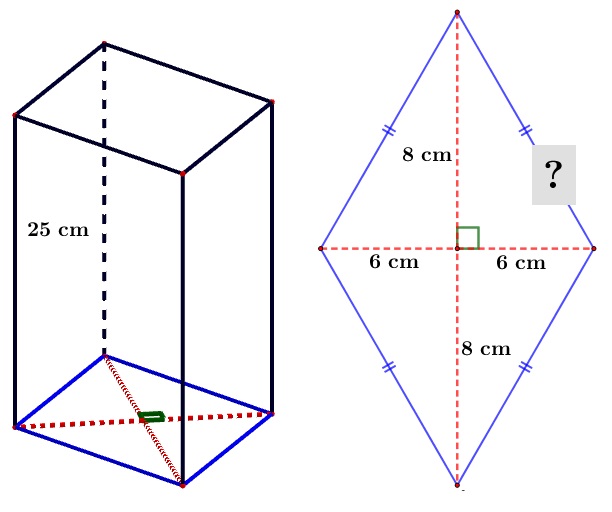
Untuk menghitung sisi belahketupat yang belum diketahui di atas dapat kita gunakan teorema pythagoras, yaitu:
$ \begin{align}
\sqrt{6^{2}+8^{2}} &= \sqrt{36+64} \\
&= \sqrt{100} =10
\end{align} $
Luas permukaan prisma;
$ \begin{align}
L & =2 \times \text{Luas belahketupat} + 4 \times \text{Luas persegipanjang} \\
L & =2 \times \left[ \frac{1}{2} \times 12 \times 16 \right] + 4 \times \left[ 25 \times 10 \right] \\
L & =192 + 100 \\
& = 1.192
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(B)\ 1.192\ \text{cm}^{2}$
27. Soal UN Matematika SMP 2014 |*Soal Lengkap
Sebuah prisma memiliki alas berbentuk layang-layang. Panjang diagonal layang-layang tersebut $10\ \text{cm}$ dan $17\ \text{cm}$. Jika tinggi prisma $8\ \text{cm}$, maka volume adalah...
Alternatif Pembahasan:
Volume prisma adalah $\text{luas alas} \times \text{tinggi}$, untuk alas berupa layang-layang maka volume prisma adalah:
$\begin{align}
V\ &= L_{\text{layang-layang}} \times \text{tinggi} \\
&= \dfrac{1}{2} \times 10\ \text{cm} \times 17\ \text{cm} \times 8\ \text{cm} \\
&= 85\ \text{cm}^{2} \times 8\ \text{cm} \\
&= 680\ \text{cm}^{3}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 680\ \text{cm}^{3}$
28. Soal UN Matematika SMP 2014 |*Soal Lengkap
Luas seluruh permukaan limas persegi yang keliling alanya $48\ \text{cm}$ dan tinggi $8\ \text{cm}$ adalah...
Alternatif Pembahasan:
Persegi yang kelilingnya $48\ \text{cm}$ maka panjang sisinya adalah $\dfrac{48\ \text{cm}}{4}=12\ \text{cm}$. Untuk persegi yang panjang sisinya $12\ \text{cm}$ maka luasnya $12\ \text{cm} \times 12\ \text{cm} = 144\ \text{cm}^{2}$.
Tinggi segitiga $CBT$ adalah $TE$, sehingga panjangnya adalah:
$\begin{align}
TE^{2}\ &= OT^{2}+OE^{2} \\
TE^{2}\ &= 8^{2}+6^{2} \\
TE^{2}\ &= 64+36 \\
TE^{2}\ &= 100 \\
TE\ &= \sqrt{100}=10 \\
\hline
\left[ BCT \right]\ &= \dfrac{1}{2} \times BC \times TE \\
&= \dfrac{1}{2} \times 12 \times 10 \\
&= 60\ \text{cm}^{2}
\end{align}$
Luas seluruh permukaan limas adalah $144\ \text{cm}^{2} + 4 \times 60\ \text{cm}^{2}=384\ \text{cm}^{2}$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ 384\ \text{cm}^{2}$
29. Soal UN Matematika SMP 2014 |*Soal Lengkap
Banyak sisi dan rusuk pada prisma segi-6 adalah...
Alternatif Pembahasan:
Prisma segi-6 memiliki alas segi-6 sehingga sisi tegaknya ada $6$, sisi alas ada $1$ dan sisi atas ada $1$ sehingga banyak sisinya ada $6+1+1=8$.
Banyak rusuk pada sisi alas ada $6$, rusuk sisik atas ada $6$, dan sisi tegak sebanyak titik sudut alas yaitu $6$ sehingga banyak rusuk keseluruhan adalah $6+6+6=18$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ 8\ \text{dan}\ 18$
30. Soal UN Matematika SMP 2014 |*Soal Lengkap
Yang merupakan jaring-jaring kubus adalah...
Alternatif Pembahasan:
Jika dicoba merangkai jaring-jaring di atas menjadi sebuah kubus yang memungkinkan adalah jaring-jaring nomor $(i)$ dan $(iv)$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ (i)\ \text{dan}\ (iv)$
31. Soal UN Matematika SMP 2013 |*Soal Lengkap
Kawat sepanjang $12\ \text{meter}$ akan dibuat kerangka balok yang berukuran panjang $27\ \text{cm}$, lebar $21\ \text{cm}$, dan tinggi $12\ \text{cm}$. Paling banyak kerangka balok yang dapat dibuat adalah...
Alternatif Pembahasan:
Rangka balok terdiri dari tiga bagian, gambarannya dapat kita lihat pada gambar di bawah ini:
$\begin{align}
K_{\text{balok}} &= 4 \times p +4 \times l + 4 \times t \\
&= 4 \times 27\ \text{cm} + 4 \times 21\ \text{cm} + 4 \times 12\ \text{cm} \\
&= 108\ \text{cm} + 84\ \text{cm} + 48\ \text{cm} \\
&= 240\ \text{cm}=2,4\ \text{m}
\end{align}$
Banyak rangka balok yang dapat dibuat adalah $\dfrac{12\ \text{m}}{2,4\ \text{m}}=5$, sehingga banyak rangka balok yang dapat dibuat paling banyak adalah $5$.
$\therefore$ Pilihan yang sesuai adalah $(B)\ 5\ \text{buah}$
32. Soal UN Matematika SMP 2013 |*Soal Lengkap
Perhatikan limas $TABCD$ alasnya berbentuk persegi. Keliling alas limas $72\ \text{cm}$ dan panjang $TP=15\ \text{cm}$. Volume limas tersebut adalah...
Alternatif Pembahasan:
Volume limas adalah $\dfrac{1}{3}$ times \text{Luas Alas} \times Tinggi$,
Karena alas limas sebuah persegi dengan keliling $72\ \text{cm}$, panjang sisinya adalah $\dfrac{72\ \text{cm}}{4}=18\ \text{cm}$ dan luasnya adalah $\left( 18\ \text{cm} \right)^{2}=324\ \text{cm}^{2}$.
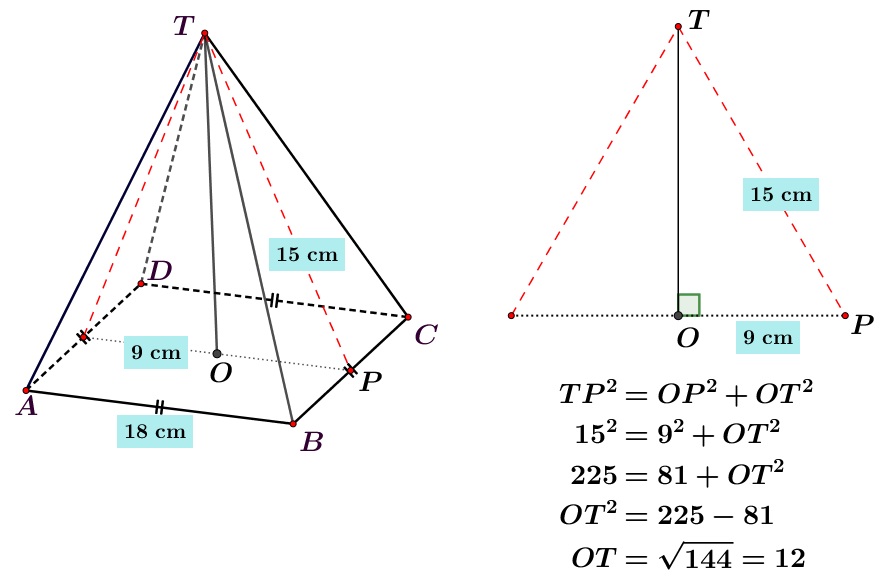
Volume limas adalah:
$\begin{align}
V &= \dfrac{1}{3} times \text{Luas Alas} \times \text{Tinggi} \\
&= \dfrac{1}{3} times 18 \times 18 \times 12 \\
&= 4 \times 324 \\
&= 1.296
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 1.296\ \text{cm}^{3}$
33. Soal UN Matematika SMP 2014 |*Soal Lengkap
Panjang diagonal sisi kubus $8\sqrt{2}\ \text{cm}$. Luas seluruh permukaan kubus adalah...
Alternatif Pembahasan:
Diagonal sisi kubus $8\sqrt{2}$ maka panjang sisi rusuk kubus adalah $8$. Dengan rusuk kubus $8$ maka luas seluruh permukaan kubus adalah:
$\begin{align}
L &= 6 \times \text{Luas Sisi} \\
&= 6 \times 8 \times 8 \\
&= 4 \times 64 \\
&= 384
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 384\ \text{cm}^{2}$
34. Soal UN Matematika SMP 2013 |*Soal Lengkap
Sebuah aula berbentuk balok dengan ukuran panjang $6\ \text{meter}$, lebar $10\ \text{meter}$, dan tinggi $5\ \text{meter}$. Dinding bagian dalamnya akan dicat dengan biaya $\text{Rp}40.000,00$ per meter persegi. Seluruh biaya pengecatan aula tersebut adalah...
Alternatif Pembahasan:
Untuk menghitung biaya pengecatan aula, kita perlu hitung luas permukaan yang akan di cat. Karena aula berbentuk balok dan dinding bagian dalam akan di cat maka luas permukaan yang akan di cat adalah:
$ \begin{align}
L &= 2 \left( 6\ \text{m} \times 5\ \text{m} \right)+ 2 \left( 10\ \text{m} \times 5\ \text{m} \right) \\
&= 2 \left( 30\ \text{m}^{2} \right)+ 2 \left( 50\ \text{m}^{2} \right) \\
&= 60\ \text{m}^{2} + 100\ \text{m}^{2} \\
&= 160\ \text{m}^{2}
\end{align} $
Biaya pengecatan $\text{Rp}40.000,00$ per meter persegi maka untuk luas $160\ \text{m}^{2}$ biaya yang diperlukan adalah $160 \times \text{Rp}40.000,00=\text{Rp}6.400.000,00$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{Rp}6.400.000,00$
35. Soal UN Matematika SMP 2012 |*Soal Lengkap
Perhatikan gambar di bawah ini!
Yang merupakan jaring-jaring balok adalah...
Alternatif Pembahasan:
Jika dicoba merangkai jaring-jaring di atas menjadi sebuah kubus yang memungkinkan adalah jaring-jaring nomor $(i)$ dan $(iv)$.
$\therefore$ Pilihan yang sesuai adalah $(D)\ (i)\ \text{dan}\ (iv)$
36. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Perhatikan gambar berikut. Agar terbentuk jaring-jaring balok, bidang yang harus dihilangkan adalah nomor...
Alternatif Pembahasan:
Jika dicoba merangkai jaring-jaring balok di atas menjadi sebuah balok yang, mungkin dihilangkan dari pilihan yang ada adalah bidang nomor $1,\ 7,\ 9$.
$\therefore$ Pilihan yang sesuai adalah $(B)\ 1,\ 7,\ 9$
37. Soal UN Matematika SMP 2011 |*Soal Lengkap
Perhatikan gambar di bawah ini!
Agar terbentuk jaring-jaring balok, bidang yang harus dihilangkan bernomor...
Alternatif Pembahasan:
Jika dicoba merangkai jaring-jaring balok di atas menjadi sebuah balok yang, mungkin dihilangkan dari pilihan yang ada adalah bidang nomor $1,4,9$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ 1,4,9$
38. Soal UN Matematika SMP 2011 |*Soal Lengkap
Perhatikan gambar berikut!
Daerah yang diarsir adalah...
Alternatif Pembahasan:
Berdasarkan informasi pada gambar, daerah yang diarsir adalah bidang diagonal.
Bidang diagonal adalah bidang yang dibentuk oleh diagonal bidang dan rusuk dan membagi bangun ruang menjadi dua bagian (bidang irisan suatu bangun ruang).
$\therefore$ Pilihan yang sesuai adalah $(B)\ \text{bidang diagonal}$
39. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2006 |*Soal Lengkap
$ABCD$ adalah bujur sangkar dengan sisi $14$ cm, merupakan alas limas dengan puncak $P$ yang tingginya $6$ cm. Di dalam bujur sangkar tersebut dibuat lingkaran yang menyinggung keempat sisi bujur sangkar tadi. Lingkaran ini merupakan alas kerucut dengan puncak $P$. Jika $\pi=\dfrac{22}{7}$, maka volume kerucut tersebut adalah...
Alternatif Pembahasan:
Lingkaran berada dalam bujur sangkar dan menyingung keempat sisi persegi sehingga jari-jari lingkaran adalah setengah sisi persegi yaitu $7$ cm.
$\begin{align}
V_{k} & = \dfrac{1}{3} \cdot L_{\text{alas}} \cdot t \\
V_{k} & = \dfrac{1}{3} pi r^{2} t \\
& = \dfrac{1}{3} left(\dfrac{22}{7} \right) (49) (6) \\
& = \dfrac{1}{3} (22) (7) (6) \\
& = (22) (7) (2) \\
& = 308
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 308\ cm^{3}$
40. Model Soal Tes Masuk YASOP - SMAN 2 Balige 2004 |*Soal Lengkap
Sebuah kerucut yang berjari-jari $3$ cm dan tingginya $4$ cm, luas permukaannya adalah...
Alternatif Pembahasan:
Untuk $r=3$ dan $t=4$ dapat kita peroleh garis pelukis $s$, yaitu:
$\begin{align}
s^{2} & =t^{2}+r^{2} \\
& = 4^{2}+3^{2} \\
& = 16+9 \\
& = 25 \\
s & = \sqrt{25}=5
\end{align}$
Luas permukaan kerucut adalah luas alas kerucut ditambah luas selimut kerucut, yaitu:
$\begin{align}
L & = \pi \cdot r^{2} + \pi \cdot r \cdot s \\
& = \pi \cdot 3^{2} + \pi \cdot 3 \cdot 5 \\
& = 9 \pi + 15 \pi \\
& = 24 \pi
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 24 \pi\ cm^{2}$
Catatan Soal dan Pembahasan Bangun Ruang Sisi Datar dan Sisi Lengkung Matematika SMP di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.
Ayo Share (Berbagi) Satu Hal Baik.
Keberhasilan bukanlah milik orang yang pintar, tapi milik orang yang tekun dan tidak pernah menyerah.
