Calon guru belajar matematika dasar SMP lewat soal dan pembahasan Bangun Ruang Sisi Datar (BRSD) dan Bangun Ruang Sisi Lengkung (BRSL) pada matematika SMP. Apa yang diharapkan setelah mempelajari materi ini, yaitu dengan aturan yang berlaku dan kreativitas berpikir kita dapat menyelesaikan masalah yang berkaitan dengan luas permukaan dan volume bangun ruang sisi datar (kubus, balok, prisma dan limas) dan bangun ruang sisi lengkung (tabung, kerucut, dan bola), serta gabungan beberapa bangun ruang.
Soal matematika dasar bangun ruang sisi datar atau bangun ruang sisi lengkung untuk SMP kita pilih dari soal-soal yang sudah pernah diujikan pada soal Ujian Sekolah matematika SMP, soal Ujian Nasional matematika SMP, atau soal ujian seleksi akademik masuk SMA Unggulan atau SMA Plus.
BANGUN RUANG SISI DATAR (BRSD)
Bangun ruang yang dikategorikan dengan bangun ruang sisi datar adalah kubus, balok, prisma dan limas.
KUBUS
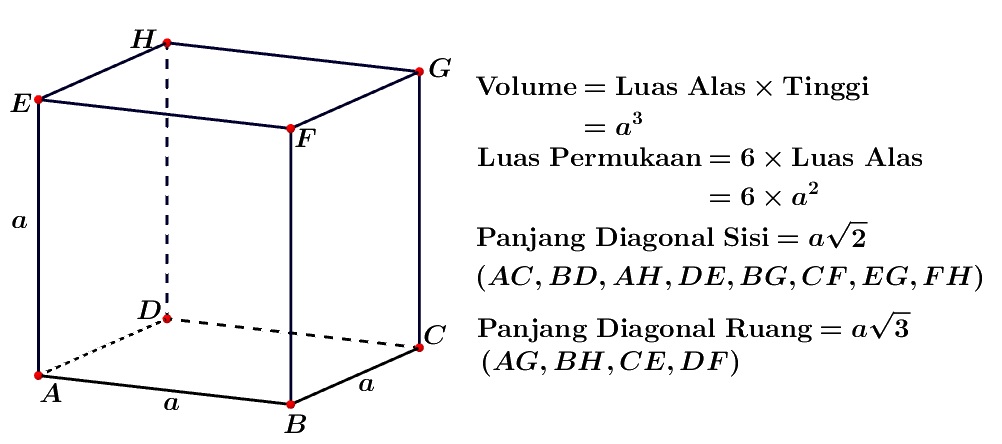
BALOK
PRISMA
LIMAS
BANGUN RUANG SISI LENGKUNG (BRSL)
Bangun ruang yang dikategorikan dengan bangun ruang sisi lengkun adalah tabung, kerucut dan bola.
TABUNG
KERUCUT
BOLA
Pembahasan Soal Bangun Ruang Sisi Datar dan Sisi Lengkung Matematika SMP
Untuk menambah pemahaman kita terkait Bangun Ruang Sisi Datar dan Sisi Lengkung, mari kita simak beberapa soal latihan di bawah ini. Soal latihan kita pilih dari soal-soal yang diujikan pada Ujian Nasional matematika SMP atau Ujian Sekolah matematika SMP.
Catatan matematika SMP tentang soal dan pembahasan Bangun Ruang Sisi Datar dan Sisi Lengkung ini kita bagi menjadi dua catatan, agar dapat dicoba dan dipelajari secara optimal.
Soal latihan Bangun Ruang Sisi Datar dan Sisi Lengkung berikut ini, silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan Periksa Jawaban dan jika hasilnya belum memuaskan, pilih Ulangi Tes untuk tes ulang.
Tunjukkan Kemampuan Terbaikmu!
| Nama Peserta : | |
| Tanggal Tes : | |
| Jumlah Soal : | 35 soal |
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.
41. Soal UNBK Matematika SMP 2019 |*Soal Lengkap
Ayah membuat topi dari kain dengan bentuk seperti gambar.
Luas kain yang diperlukan untuk membuat topi tersebut adalah...
Alternatif Pembahasan:
Untuk menghitung banyak kain yang dibutuhkan untuk membuat seperti topi, sama dengan mencari luas selimut kerucut dengan jari-jari $10\ \text{cm}$ dan luas selisih dua lingkaran.
Luas selimut kerucut
$\begin{align}
L &= \pi\ \cdot r \cdot s\\
&= 3,14 \cdot 10\ \text{cm} \cdot 26\ \text{cm} \\
&= 816,4\ \text{cm}{2}
\end{align}$
Luas selisih dua lingkaran
$\begin{align}
L &= L_{2}-L_{1} \\
&= \pi \cdot r^{2}_{2}-\pi \cdot r^{2}_{1} \\
&= 3,14 \cdot 20^{2}- 3,14 \cdot 10^{2} \\
&= 3,14 \cdot 400- 3,14 \cdot 100 \\
&= 1,256- 314 \\
&= 942\ \text{cm}^{2} \\
\end{align}$
Total luas kain adalah $816,4+942=1.758,4\ \text{cm}^{2}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 1.758,4\ \text{cm}^{2}$
42. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap
Perhatikan gambar!
Luas seluruh permukaan bangun gabungan tabung dan setengah bola adalah...
Alternatif Pembahasan:
Pada gambar di atas terdapat dua bangun, yaitu tabung yang ditutup dengan setengah bola.
Pertama kita hitung luas permukaan setengah bola.
$\begin{align}
L_{b} & = \frac{1}{2} \cdot 4 \pi \cdot r^{2} \\
& = \frac{1}{2} \cdot 4 \frac{22}{7} \cdot (7)^{2} \\
& = 2 \cdot 22 \cdot 7 \\
& = 308
\end{align}$
Kedua kita hitung luas permukaan tabung tanpa tutup.
$\begin{align}
L_{t} & = \pi \cdot r^{2} + t \cdot 2 \pi r \\
& = \frac{22}{7} \cdot (7)^{2} + 19 \cdot 2 \cdot \frac{22}{7} \cdot 7 \\
& = 22 \cdot 7 + 38 \cdot 22 \\
& = 154 + 836 \\
& = 990
\end{align}$
Luas seluruh permukaan bangun adalah $990+308=1.298$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 1.298\ \text{cm}^{2}$
43. Soal UNBK Matematika SMP 2018 |*Soal Lengkap
Perhatikan gambar!
Luas seluruh permukaan bangun gabungan tabung dan setengah bola adalah...
Alternatif Pembahasan:
Pada gambar di atas terdapat dua bangun, yaitu tabung yang ditutup dengan setengah bola.
Pertama kita hitung luas permukaan setengah bola.
$\begin{align}
L_{b} & = \frac{1}{2} \cdot 4 \pi \cdot r^{2} \\
& = \frac{1}{2} \cdot 4 \frac{22}{7} \cdot (7)^{2} \\
& = 2 \cdot 22 \cdot 7 \\
& = 308
\end{align}$
Kedua kita hitung luas permukaan tabung tanpa tutup.
$\begin{align}
L_{t} & = \pi \cdot r^{2} + t \cdot 2 \pi r \\
& = \frac{22}{7} \cdot (7)^{2} + 10 \cdot 2 \cdot \frac{22}{7} \cdot 7 \\
& = 22 \cdot 7 + 20 \cdot 22 \\
& = 154 + 440 \\
& = 594
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 594\ cm^{2}$
44. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap
Sebuah kerucut mempunyai volume $50\ \text{cm}^{3}$. Jika diameter alas kerucut diperbesar $2$ kali dan tingginya diperbesar $3$ kali, maka volume kerucut yang baru adalah...
Alternatif Pembahasan:
Rumus bangun ruang sampai SMP masih bisa kita bagi menjadi 3 kategori;
- Kelompok Prisma: $V= \text{Luas Alas} \times \text{Tinggi}$
- Kelompok Limas: $V= \frac{1}{3} times \text{Luas Alas} \times \text{Tinggi}$
- Bola: $V= \frac{4}{3} times \pi\ r^{3}$
Kerucut masuk kedalam kategori Limas;
$V= \frac{1}{3} times \text{Luas Alas} \times \text{Tinggi}$
Misalkan:
$d_{o}:\ \text{diameter mula-mula}$;
$t_{o}:\ \text{tinggi mula-mula}$;
$V_{o}:\ \text{Volume mula-mula}$;
$\begin{align}
V_{o} &= \dfrac{1}{3} times \pi\ r_{o}^{2} \times t_{o} \\
50\ \text{cm}^{3} &= \frac{1}{3} times \pi\ \left(\frac{d_{o}}{2} \right)^{2} \times t_{o} \\
50\ \text{cm}^{3} &= \frac{1}{3} times \frac{1}{4} \pi\ d_{o}^{2} \times t_{o} \\
50\ \text{cm}^{3} &= \frac{1}{12} \times \pi\ d_{o}^{2} \times t_{o} \\
50\ \text{cm}^{3} times 12 &= \pi\ d_{o}^{2} \times t_{o} \\
600\ \text{cm}^{3} &= \pi\ d_{o}^{2} \times t_{o}
\end{align}$
Misalkan:
$d_{t}:$ diameter setelah perubahan;
$t_{t}:$ tinggi setelah perubahan;
$V_{t}:$ Volume setelah perubahan;
$V_{t}= \frac{1}{3} times \pi\ r_{t}^{2} \times t_{t}$
Karena diameter alas kerucut diperbesar $2$ kali $(d_{t}=2d_{o})$ dan tingginya diperbesar $3$ kali $(t_{t}=3t_{o})$, maka:
$\begin{align}
V_{t} &= \frac{1}{3} times \pi\ r_{t}^{2} \times t_{t} \\
V_{t} &= \frac{1}{3} pi\ \left( \frac{d_{t}}{2} \right)^{2} \times t_{t} \\
V_{t} &= \frac{1}{3} pi\ \left( \frac{2d_{o}}{2} \right)^{2} \times 3t_{o} \\
V_{t} &= \frac{1}{3} pi\ d_{o}^{2} \times 3t_{o} \\
V_{t} &= \frac{3}{3} pi\ d_{o}^{2} \times t_{o} \\
V_{t} &= 600
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 600\ \text{cm}^{3}$
45. Soal Masuk Asrama YASOP - SMAN 2 Balige 2006 |*Soal Lengkap
Volume sebuah kerucut adalah $314\ \text{cm}^{2}$. Jika jari-jarinya adalah $5\ \text{cm}$ dan $\pi=3,14$ maka panjang garis pelukisnya adalah...
Alternatif Pembahasan:
Garis pelukis kerucut $(s)$ adalah jumlah kuadrat dari jari-jari dan tinggi kerucut;
Dengan Volume $314\ \text{cm}^{2}$ maka
$\begin{align}
V & = \dfrac{1}{3} pi r^{2} t \\
314 & = \dfrac{1}{3} (3,14) (25) (t) \\
314 & = \dfrac{1}{3} (3,14) (25) (t) \\
t & = \dfrac{314 \times 3}{3,14 \times 25} \\
t & = \dfrac{300}{25} \\
t & = 12
\end{align}$
$\begin{align}
s^{2} & = t^{2}+r^{2} \\
s^{2} & = 12^{2}+5^{2} \\
s^{2} & = 144+25 \\
s^{2} & = 169 \\
s & = \sqrt{169} \\
s & = 13
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 13$
46. Soal UN Matematika SMP 2018 |*Soal Lengkap
Sebuah tabung berdiameter $14\ \text{cm}$ dengan tinggi $34\ \text{cm}$. Luas seluruh permukaan tabung adalah...$\left(\pi=\dfrac{22}{7} \right)$
Alternatif Pembahasan:
Luas permukaan tabung adalah luas selimut berupa persegipanjang ditambah dua kali luas alas yang berupa lingkaran:
$\begin{align}
L_{t} & = t \cdot 2 \pi r + 2 \pi \cdot r^{2} \\
L_{t} & = 34 \cdot 2 \left( \dfrac{22}{7} \right) \left( 7 \right) + 2 \left( \dfrac{22}{7} \right) \cdot \left( 7 \right)^{2} \\
& = 68 \left( 22 \right) + 2 \left( 22 \right) \cdot \left( 7 \right) \\
& = 1.496 + 308 \\
& = 1.804
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 1.804\ \text{cm}^{2}$
47. Soal UN Matematika SMP 2017 |*Soal Lengkap
Kubah masjid berbentuk setengah bola yang akan dilapisi aluminium di sisi luarnya. Panjang jari-jari kubah $3,5\ \text{meter}$, luas minimal yang dibutuhkan adalah...
Alternatif Pembahasan:
Luas permukaan kubah masjid berbentuk setengah bola, luas permukaannya adalah:
$\begin{align}
L_{b} & = \dfrac{1}{2} \cdot 4 \pi \cdot r^{2} \\
& = \dfrac{1}{2} \cdot 4 \cdot \dfrac{22}{7} \cdot (3,5)^{2} \\
& = 2 \cdot \dfrac{22}{7} \cdot (3,5) \cdot (3,5) \\
& = \dfrac{22}{7} \cdot (7) \cdot (3,5) \\
& = 22 \cdot (3,5) \\
& = 77
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 77\ \text{m}^{2}$
48. Soal UN Matematika SMP 2016 |*Soal Lengkap
Sebuah kerucut mempunyai volume $27\ \text{cm}^{3}$. Jika diameter alas kerucut diperbesar $2$ kali dan tingginya diperbesar $3$ kali, maka volume kerucut yang baru adalah...
Alternatif Pembahasan:
Rumus bangun ruang sampai SMP masih bisa kita bagi menjadi 3 kategori;
- Kelompok Prisma: $V= \text{Luas Alas} \times \text{Tinggi}$
- Kelompok Limas: $V= \frac{1}{3} times \text{Luas Alas} \times \text{Tinggi}$
- Bola: $V= \frac{4}{3} times \pi\ r^{3}$
Kerucut masuk kedalam kategori Limas;
$V= \frac{1}{3} times \text{Luas Alas} \times \text{Tinggi}$
Misalkan:
$d_{o}:\ \text{diameter mula-mula}$;
$t_{o}:\ \text{tinggi mula-mula}$;
$V_{o}:\ \text{Volume mula-mula}$;
$\begin{align} V_{o} &= \dfrac{1}{3} times \pi\ r_{o}^{2} \times t_{o} \\ 27\ \text{cm}^{3} &= \frac{1}{3} times \pi\ \left(\frac{d_{o}}{2} \right)^{2} \times t_{o} \\ 27\ \text{cm}^{3} &= \frac{1}{3} times \frac{1}{4} \pi\ d_{o}^{2} \times t_{o} \\ 27\ \text{cm}^{3} &= \frac{1}{12} \times \pi\ d_{o}^{2} \times t_{o} \\ 27\ \text{cm}^{3} times 12 &= \pi\ d_{o}^{2} \times t_{o} \\ 324\ \text{cm}^{3} &= \pi\ d_{o}^{2} \times t_{o} \end{align}$
Misalkan:
$d_{t}:$ diameter setelah perubahan;
$t_{t}:$ tinggi setelah perubahan;
$V_{t}:$ Volume setelah perubahan;
$V_{t}= \frac{1}{3} times \pi\ r_{t}^{2} \times t_{t}$
Karena diameter alas kerucut diperbesar $2$ kali $(d_{t}=2d_{o})$ dan tingginya diperbesar $3$ kali $(t_{t}=3t_{o})$, maka:
$\begin{align}
V_{t} &= \frac{1}{3} times \pi\ r_{t}^{2} \times t_{t} \\
V_{t} &= \frac{1}{3} pi\ \left( \frac{d_{t}}{2} \right)^{2} \times t_{t} \\
V_{t} &= \frac{1}{3} pi\ \left( \frac{2d_{o}}{2} \right)^{2} \times 3t_{o} \\
V_{t} &= \frac{1}{3} pi\ d_{o}^{2} \times 3t_{o} \\
V_{t} &= \frac{3}{3} pi\ d_{o}^{2} \times t_{o} \\
V_{t} &= 324\ \text{cm}^{3}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 324\ \text{cm}^{3}$
49. Soal UN Matematika SMP 2015 |*Soal Lengkap
Sebuah benda berbentuk belahan bola dengan panjang diameter $18\ \text{cm}$. Volume benda adalah...
Alternatif Pembahasan:
Volume benda berbentuk setengah bola adalah:
$\begin{align}
V_{b} & = \dfrac{1}{2} \times \dfrac{4}{3} times \pi\ r^{3} \\
& = \dfrac{1}{2} \times \dfrac{4}{3} times \pi\ \left( 9\ \text{cm} \right)^{3} \\
& = \dfrac{2}{3} times \pi\ \times 729\ \text{cm}^{3}$ \\
& = 486\ \text{cm}^{3}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 486 \pi \ \text{cm}^{3}$
50. Soal UN Matematika SMP 2015 |*Soal Lengkap
Panjang jari-jari alas kerucut $7\ \text{cm}$. Jika tinggi kerucut $9\ \text{cm}$ maka volume kerucut adalah...
Alternatif Pembahasan:
Volume kerucut dengan $r=7\ \text{cm}$, $t=9\ \text{cm}$ dan $\pi$ yang kita gunakan $\pi=\dfrac{22}{7}$ adalah...
$\begin{align}
V_{k} & = \dfrac{1}{3} \cdot L_{\text{alas}} \cdot t \\
V_{k} & = \dfrac{1}{3} \cdot \pi \cdot r^{2} \cdot t \\
& = \dfrac{1}{3} \cdot \left( \dfrac{22}{7} \right) \cdot 7^{2} \cdot 9 \\
& = \left( \dfrac{22}{7} \right) \cdot 7 \cdot 7 \cdot 3 \\
& = (22) (7) (3) \\
& = 462
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 462\ cm^{3}$
51. Soal UN Matematika SMP 2015 |*Soal Lengkap
Perhatikan gambar!
Jika luas permukaan bola $160\ \text{cm}^{2}$, maka luas seluruh permukaan tabung adalah...
Alternatif Pembahasan:
Luas permukaan bola adalah $160\ \text{cm}^{2}$ sehingga dapat kita peroleh:
$\begin{align}
L_{b} & = 4 \cdot \pi \cdot r^{2} \\
160 & = 4 \cdot \pi \cdot r^{2} \\
\dfrac{160}{4} & = \pi \cdot r^{2} \\
40 & = \pi \cdot r^{2}
\end{align}$
Karena bola menyinggung sisi-sisi tabung maka tinggi tabung merupakan diameter bola.
$\begin{align}
L_{t} & = 2 \cdot \pi \cdot r^{2} + t \cdot 2 \pi r \\
& = 2 \cdot 40 + 2r \cdot 2 \pi \cdot r \\
& = 80 + 4 \cdot \pi \cdot r^{2} \\
& = 80 + 4 \cdot 40 \\
& = 40 + 160 \\
& = 200
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 200\ \text{cm}^{2}$
52. Soal UN Matematika SMP 2014 |*Soal Lengkap
Sebuah prisma memiliki alas berbentuk layang-layang. Panjang diagonal layang-layang tersebut $10\ \text{cm}$ dan $17\ \text{cm}$. Jika tinggi prisma $8\ \text{cm}$, maka volume adalah...
Alternatif Pembahasan:
Volume prisma adalah Luas alas $\times$ tinggi, sehingga dengan bentuk alas layang-layang volume prisma adalah:
$\begin{align}
V_{p} & = L_{\text{layang-layang}} \times t \\
& = \dfrac{1}{2} \cdot 10 \cdot 17 \cdot 8 \\
& = 170 \cdot 4 \\
& = 680
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 680\ \text{cm}^{3}$
53. Soal UN Matematika SMP 2014 |*Soal Lengkap
Perhatikan gambar gabungan kerucut dan tabung di bawah ini!
Luas permukaan bangun tersebut adalah...
Alternatif Pembahasan:
Bangun terdiri dari tabung dan kerucut dimana kerucut hanya selimut dan tabung tanpa tutup sehingga luas permukaan adalah:
Luas selimut kerucut
$\begin{align}
L_{k} &= \pi\ \cdot r \cdot s \\
&= \dfrac{22}{7} \cdot 7 \cdot 25 \\
&= 22 \cdot 25=550
\end{align}$
Luas permukaan tabung
$\begin{align}
L_{t} & = \pi \cdot r^{2} + t \cdot 2 \pi r \\
& = \dfrac{22}{7} \cdot 7^{2} + 12 \cdot 2 \cdot \dfrac{22}{7} \cdot 7 \\
& = 22 \cdot 7 + 24 \cdot 22 \\
& = 154 + 528 \\
& = 682
\end{align}$
Total luas permukaan adalah $682+550=1.232\ \text{cm}^{2}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 1.232\ \text{cm}^{2}\ \text{cm}^{2}$
54. Soal UN Matematika SMP 2013 |*Soal Lengkap
Sebuah bola akan dimasukkan ke dalam kubus dengan panjang rusuk $20\ \text{cm}$. Volume bola terbesar yang dapat masuk ke dalam kubus adalah...$\left(\pi=3,14 \right)$
Alternatif Pembahasan:
Bola akan dimasukkan ke dalam kubus dengan panjang rusuk kubus $20\ \text{cm}$ maka jari-jari bola yang bisa masuk paling besar adalah $10\ \text{cm}$. Sehingga volume bola terbesar adalah:
$\begin{align}
V_{b} & = \dfrac{4}{3} \cdot \pi \cdot r^{3} \\
& = \dfrac{4}{3} \cdot 3,14 \cdot (10)^{3} \\
& = \dfrac{4}{3} \cdot 3,14 \cdot 1.000 \\
& = \dfrac{4}{3} \cdot 3.140 \\
& = \dfrac{12.560}{3} \\
& = 4.186,67
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 4.186,67\ \text{cm}^{3}$
55. Soal UN Matematika SMP 2013 |*Soal Lengkap
Sebuah tabung berdiameter $28\ \text{cm}$ dengan tinggi $26\ \text{cm}$. Luas seluruh permukaan tabung adalah...$\left(\pi=\dfrac{22}{7} \right)$
Alternatif Pembahasan:
Luas seluruh permukaan tabung adalah:
$\begin{align}
L_{t} & = t \cdot 2 \pi r + 2 \pi \cdot r^{2} \\
L_{t} & = 26 \cdot 2 \cdot \left( \dfrac{22}{7} \right) \left( 14 \right) + 2 \cdot \left( \dfrac{22}{7} \right) \cdot \left( 14 \right)^{2} \\
& = 52 \cdot \left( 22 \right) \left( 2 \right) +2 \cdot \left( 22 \right) \cdot \left( 2 \right) \cdot \left( 14 \right) \\
& = 52 \cdot 44 + 44 \cdot 28 \\
& = 44 \left ( 52 + 28 \right) \\
& = 3.520
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 3.520\ \text{cm}^{2}$
56. Soal UN Matematika SMP 2012 |*Soal Lengkap
Volume kerucut yang panjang diameter alasnya $20\ \text{cm}$ dan tinggi $12\ \text{cm}$ adalah... $\left( \pi=3,14 \right)$
Alternatif Pembahasan:
Volume kerucut dengan $d=20\ \text{cm}$ maka $r=10\ \text{cm}$ dan $t=12\ \text{cm}$ dengan $\pi$ yang kita gunakan $\pi=3,14$ adalah...
$\begin{align}
V_{k} & = \dfrac{1}{3} \cdot L_{\text{alas}} \cdot t \\
V_{k} & = \dfrac{1}{3} \cdot \pi \cdot r^{2} \cdot t \\
& = \dfrac{1}{3} \cdot \left( 3,14 \right) \cdot 10^{2} \cdot 12 \\
& = 4 \cdot 3,14 \cdot 100 \\
& = 4 \cdot 314 \\
& = 1.256
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 1.256\ \text{cm}^{3}$
57. Soal UN Matematika SMP 2012 |*Soal Lengkap
Volume bola terbesar yang dapat dimasukkan ke dalam dus berbentuk kubus dengan panjang rusuk $12\ \text{cm}$ adalah...
Alternatif Pembahasan:
Bola akan dimasukkan ke dalam dus berbentuk kubus dengan panjang rusuk kubus $12\ \text{cm}$ maka jari-jari bola yang bisa masuk paling besar adalah $6\ \text{cm}$. Sehingga volume bola terbesar adalah:
$\begin{align}
V_{b} & = \dfrac{4}{3} \cdot \pi \cdot r^{3} \\
& = \dfrac{4}{3} \cdot \pi \cdot (6)^{3} \\
& = \dfrac{4}{3} \cdot \pi \cdot 216 \\
& = 4 \pi \cdot 72 \\
& = 288\pi
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 288\pi\ \text{cm}^{3}$
58. Soal UN Matematika SMP 2012 |*Soal Lengkap
Perhatikan gambar!
Jika jari-jari bola $12\ \text{cm}^{2}$, maka luas seluruh permukaan tabung adalah...
Alternatif Pembahasan:
Bola dalam tabung dengan jari-jari $12\ \text{cm}$ sehingga jari-jari alas tabung adalah $12\ \text{cm}$ dan tinggi tabung $24\ \text{cm}$:
$\begin{align}
L_{t} & = 2 \cdot \pi \cdot r^{2} + t \cdot 2 \pi r \\
& = 2 \cdot \pi \cdot 12^{2} + 24 \cdot 2 \pi \cdot 12 \\
& = 2 \pi \cdot 144 + 48 \cdot \pi \cdot 12 \\
& = 288\pi + 576 \pi \\
& = 864 \pi
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 864\pi\ \text{cm}^{2}$
59. Soal UN Matematika SMP 2011 |*Soal Lengkap
Ke dalam tabung berisi air setinggi $30\ \text{cm}$ dimasukkan $6$ bola besi yang masing-masing berjari-jari $7\ \text{cm}$. Jika diameter tabung $28\ \text{cm}$, tinggi air dalam tabung setelah dimasukkan enam bola besi adalah...
Alternatif Pembahasan:
Volume $6$ bola besi yang berjari-jari $7\ \text{cm}$ adalah:
$\begin{align}
V_{b} & = 6 \times \dfrac{4}{3} \cdot \pi \cdot r^{3} \\
& = 8 \cdot \pi \cdot (7)^{3} \\
& = 8 \cdot 343 \pi \\
& = 2.744 \pi
\end{align}$
Volume air dalam tabung adalah volume tabung dengan tinggi air $30\ \text{cm}$ dan $r=14\ \text{cm}$:
$\begin{align}
V_{a} & = \pi \cdot r^{2} \cdot t \\
& = \pi \cdot 14^{2} \cdot 30 \\
& = \pi \cdot 196 \cdot 30 \\
& = 5.880 \pi
\end{align}$
Volume di dalam tabung setelah dimasukkan $6$ bola adalah volue air ditambah volume $6$ bola yaitu:
$\begin{align}
V_{a+b} & = 5.880 \pi + 2.744 \pi \\
& = 8.624 \pi
\end{align}$
Tinggi air di tabung setelah dimasukkan $6$ bola adalah $8.624 \pi$ sehingga dapat kita peroleh:
$\begin{align}
V_{a+b} & = 8.624 \pi \\
\pi \cdot 14^{2} \cdot t_{a} & = 8.624 \pi \\
\pi \cdot 196 \cdot t_{a} & = 8.624 \pi \\
t_{a} & = \dfrac{8.624 \pi}{\pi \cdot 196} \\
& = 44
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 44\ \text{cm}$
60. Soal UN Matematika SMP 2011 |*Soal Lengkap
Sebuah kerucut memiliki diameter alas $14\ \text{cm}$ dan tinggi $24\ \text{cm}$. Luas permukaan kerucut adalah...
Alternatif Pembahasan:
Untuk $d=14\ \text{cm}$ maka $r=7\ \text{cm}$, jika $t=24\ \text{cm}$ maka dapat kita peroleh garis pelukis $s$, yaitu:
$\begin{align}
s^{2} & =t^{2}+r^{2} \\
& = 24^{2}+7^{2} \\
& = 576+49 \\
& = 625 \\
s & = \sqrt{625}=25
\end{align}$
Luas permukaan kerucut adalah luas alas kerucut ditambah luas selimut kerucut, yaitu:
$\begin{align}
L & = \pi \cdot r^{2} + \pi \cdot r \cdot s \\
& = \pi \cdot 7^{2} + \pi \cdot 7 \cdot 25 \\
& = 49 \pi + 175 \pi \\
& = 224 \pi
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 224 \pi\ \text{cm}^{2}$
61. Soal UN Matematika SMP 2010 |*Soal Lengkap
Tabung dengan panjang jari-jari alas $10\ \text{cm}$ berisi minyak setinggi $14\ \text{cm}$. Ke dalam tabung itu dimasukkan minyak lagi sebanyak $1,884\ \text{liter}$. Tinggi minyak dalam tabung sekarang adalah... $\left( \pi=3,14 \right)$
Alternatif Pembahasan:
Tabung dengan jari-jari alas $10\ \text{cm}$ berisi minyak setinggi $14\ \text{cm}$, maka banyak minyak sama dengan volume tabung dengan tinggi $14\ \text{cm}$, yaitu:
$\begin{align}
V_{m} & = \pi \cdot r^{2} \cdot t_{m} \\
& = 3,14 \cdot 10^{2}\ \text{cm}^{2} \cdot 14\ \text{cm} \\
& = 3,14 \cdot 10^{2}\ \text{cm}^{2} \cdot 14\ \text{cm} \\
& = 314 \cdot 14\ \text{cm}^{3} \\
& = 4.396\ \text{cm}^{3}
\end{align}$
Ke dalam tabung itu dimasukkan minyak lagi sebanyak $1.884\ \text{liter}$. Jika ukuran liter kita ubah dalam satuan $\text{cm}^{3}$ maka akan kita peroleh:
$\begin{align}
1,884\ \text{liter} & = 1,884\ \text{dm}^{3} \\
& = 1,884 \times 10^{3}\ \text{cm}^{3} \\
& = 1.884\ \text{cm}^{3}
\end{align}$
Volume minyak dalam tabung setelah dimasukkan minyak adalah $1.884\ \text{cm}^{3}+4.396\ \text{cm}^{3}$ atau $6.280\ \text{cm}^{3}$. Sehingga tinggi minyak dalam tabung adalah:
$\begin{align}
V_{m} & = \pi \cdot r^{2} \cdot t_{m} \\
6.280 & = 3,14 \cdot 10^{2} \cdot t_{m} \\
6.280 & = 314 \cdot t_{m} \\
\dfrac{6.280}{314} & = t_{m} \\
20 & = t_{m}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 20\ \text{cm}$
62. Soal UN Matematika SMP 2010 |*Soal Lengkap
Sebuah kubah menara berbentuk setengah bola dengan diameter $7\ \text{meter}$. Bagian luar kubah tersebut akan dicat, dan setiap $11\ \text{m}^{2}$ memerlukan satu kaleng cat. Berapa kaleng cat yang diperlukan untuk mengecat kubah tersebut...$\left(\pi=\dfrac{22}{7} \right)$
Alternatif Pembahasan:
Permukaan kubah menara berbentuk setengah bola dengan diameter $7\ \text{meter}$ maka $r=3,5\ \text{meter}$, luas permukaannya adalah:
$\begin{align}
L_{b} & = \dfrac{1}{2} \cdot 4 \pi \cdot r^{2} \\
& = \dfrac{1}{2} \cdot 4 \cdot \dfrac{22}{7} \cdot (3,5)^{2} \\
& = 2 \cdot \dfrac{22}{7} \cdot (3,5) \cdot (3,5) \\
& = \dfrac{22}{7} \cdot (7) \cdot (3,5) \\
& = 22 \cdot (3,5) \\
& = 77
\end{align}$
Luas permukaan kubah adalah $77\ \text{m}^{2}$ dan untuk $11\ \text{m}^{2}$ memerlukan satu kaleng cat. Sehingga untuk $77\ \text{m}^{2}$ diperlukan $\dfrac{77}{11}=7$ kaleng cat.
$\therefore$ Pilihan yang sesuai adalah $(A)\ 7\ \text{kaleng}$
63. Soal Seleksi Masuk Asrama YASOP - SMAN 2 Balige |*Soal Lengkap
Nilai luas permukaan sebuah kubus sama dengan dua kali volume kubus tersebut. Volume kubus tersebut adalah...
Alternatif Pembahasan:
Kita ketahui bahwa untuk menghitung luas permukaan kubus dengan panjang rusuknya $a$ adalah $6 \times a \times a$. Untuk menghitung volume kubus adalah $a \times a \times a$.
Sehingga saat nilai luas permukaan sebuah kubus sama dengan dua kali volume kubus tersebut, dapat kita peroleh:
$\begin{align}
6 \times a \times a & = 2 \times a \times a \times a \\
6 \times a \times a & = 2 \times a \times a \times a \\
6 & = 2 \times a \\
3 & = a \\
\hline
V_{\text{kubus}} & = a \times a \times a \\
& = 3 \times 3 \times 3 \\
& = 27
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 27\ \text{cm}^{3}$
64. Soal Seleksi Masuk Asrama YASOP - SMAN 2 Balige |*Soal Lengkap
Tinggi air di dalam sebuah kerucut yang jari-jarinya alasnya $10\ \text{cm}$ dan tingginya $15\ \text{cm}$ adalah $12\ \text{cm}$. Jika kerucut tersebut dibalik, maka tinggi air di dalam kerucut adalah...$\left( \pi=3,14 \right)$
Alternatif Pembahasan:
Volume kerucut dengan $r=10\ \text{cm}$ dan $t=15\ \text{cm}$ adalah...
$\begin{align}
V_{k} & = \dfrac{1}{3} \cdot L_{\text{alas}} \cdot t \\
V_{k} & = \dfrac{1}{3} \cdot \pi \cdot r^{2} \cdot t \\
& = \dfrac{1}{3} \cdot \pi \cdot 10^{2} \cdot 15 \\
& = 500 \pi
\end{align}$
Dari gambar di atas dengan menggunakan perbandingan pada segitiga yang sebangun kita peroleh:
$\begin{align}
\dfrac{15}{3} & = \dfrac{10}{x} \\
x & = 2
\end{align}$
Untuk $x=2$ maka kita peroleh volume kerucut yang kosong dari air dengan $r=2\ \text{cm}$ dan $t=3\ \text{cm}$ yaitu:
$\begin{align}
V_{ko} & = \dfrac{1}{3} \cdot L_{\text{alas}} \cdot t \\
V_{ko} & = \dfrac{1}{3} \cdot \pi \cdot r^{2} \cdot t \\
& = \dfrac{1}{3} \cdot \pi \cdot 2^{2} \cdot 3 \\
& = 4 \pi
\end{align}$
Volume air adalah:
$\begin{align}
V_{air} & = V_{k}-V_{ko} \\
V_{air} & = 500 \pi-4 \pi \\
& = 496 \pi
\end{align}$
Volume air dapat juga dihitung dengan volume kerucut terpancung, yaitu $V=\frac{1}{3} \pi \times t \left( R^{2}+Rr+r^{2} \right)$
Kemudian kerucut dibalik sehingga tingggi air pada kerucut berubah seperti gambar di sebelah kanan. Dengan menggunakan perbandingan pada segitiga yang sebangun kita peroleh:
$\begin{align}
\dfrac{10}{y} & = \dfrac{15}{t_{air}} \\
y & = \dfrac{2}{3}t_{air}
\end{align}$
Volume air sebelum kerucut di balik dan sesudah kerucut dibalik adalah sama, sehingga dapat kita peroleh:
$\begin{align}
V_{air} & = \dfrac{1}{3} \cdot \pi \cdot r^{2} \cdot t \\
496 \pi & = \dfrac{1}{3} \cdot \pi \cdot y^{2} \cdot t_{air} \\
496 \pi & = \dfrac{1}{3} \cdot \pi \cdot \left( \dfrac{2}{3}t_{air} \right)^{2} \cdot t_{air} \\
496 \cdot 3 & = \dfrac{4}{9}t^{2}_{air} \cdot t_{air} \\
496 \cdot \dfrac{27}{4} & = t^{3}_{air} \\
124 \cdot 27 & = t^{3}_{air} \\
t_{air} & = \sqrt[3]{124 \cdot 27} \\
t_{air} & = 3 \sqrt[3]{124}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 3\sqrt[3]{124} \ \text{cm}$
65. Model Soal US-UM Matematika SMP 2023 |*Soal Lengkap
Perhatikan gambar berikut!
Jika panjang rusuk $AB$ adalah $6\ cm$. maka panjang diagonal $AG$ adalah...
Alternatif Pembahasan:
Diagonal ruang sebuah kubus dapat dihitung dengan menggunakan rumus yang sudah ada yaitu $a\sqrt{3}$ dimana $a$ adalah panjang rusuk kubus.
Sehingga untuk panjang rusuk $6\ cm$ maka panjang diagonal ruang adalah $6\sqrt{3}\ cm $.
Alternatif lain untuk menghitung panjang diagonal ruang sebuah kubus dapat menggunakan teorema pythagoras, cara ini juga digunakan untuk mendapatkan rumus di atas.
$ \begin{align}
AG^{2} &= CG^{2}+AC^{2} \\
AG^{2} &= CG^{2}+AB^{2}+BC^{2} \\
AG^{2} &= 6^{2}+6^{2}+6^{2} \\
AG^{2} &= 36+36+36 \\
AG &= \sqrt{36 \times 3} =6\sqrt{3}
\end{align} $
$\therefore$ Pilihan yang sesuai adalah $(C)\ 6\sqrt{3}\ cm $
66. Model Soal US-UM Matematika SMP 2023 |*Soal Lengkap
Diketahui volume sebuah bola adalah $36 \pi\ m^{3}$, luas permukaan bola tersebut adalah...
Alternatif Pembahasan:
Dari volume bola yang diketahui dapat kita peroleh:
$\begin{align}
V_{b} & = \frac{4}{3} \cdot \pi \cdot r^{3} \\
36 \pi & = \frac{4}{3} \cdot \pi \cdot r^{3} \\
36 & = \frac{4}{3} \cdot r^{3} \\
9 & = \frac{1}{3} \cdot r^{3} \\
27 & = r^{3} \longrightarrow r=3
\end{align}$
Luas permukaan bola adalah:
$\begin{align}
L_{b} & = 4 \pi \cdot r^{2} \\
& = 4 \cdot \pi \cdot (3)^{2} \\
& = 4 \cdot \pi \cdot 9 \\
& = 36 \pi
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 36\pi\ \text{m}^{2}$
67. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Disediakan kawat yang panjangnya $6\ \text{m}$, akan dibuat kerangka balok berukuran $13\ \text{cm} \times 9\ \text{cm} \times 8\ \text{cm}$. Banyak kerangka balok yang dapat dibuat dari kawat tersebut adalah...
Alternatif Pembahasan:
Rangka balok terdiri dari tiga bagian, gambarannya dapat kita lihat pada gambar di bawah ini:
$\begin{align}
K_{\text{balok}} &= 4 \times p +4 \times l + 4 \times t \\
&= 4 \times 13\ \text{cm} + 4 \times 9\ \text{cm} + 4 \times 8\ \text{cm} \\
&= 52\ \text{cm} + 36\ \text{cm} + 32\ \text{cm} \\
&= 120\ \text{cm}=1,2\ \text{m}
\end{align}$
Banyak rangka balok yang dapat dibuat adalah $\dfrac{6\ \text{m}}{1,2\ \text{m}}=5$, sehingga banyak rangka balok yang dapat dibuat paling banyak adalah $5\ \text{buah}$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ 5\ \text{buah}$
68. Soal UN Matematika SMP 2012 |*Soal Lengkap
Perhatikan bangun berikut yang terdiri dari balok dan limas!
Diketahui balok berukuran $12\ \text{cm} \times 12\ \text{cm} \times 6\ \text{cm}$. Jika tinggi limas $8\ \text{cm}$, luas permukaan bangun adalah...
Alternatif Pembahasan:
Permukaan bangun terdiri dari empat segitiga pada limas dan lima segiempat pada balok.
Luas empat segitiga adalah:
$\begin{align}
L\ &= 4 \times \left( \dfrac{1}{2} \times 12 \times 10 \right) \\
&= 240
\end{align}$
Luas lima segiempat adalah:
$\begin{align}
L\ &= 12 \times 12 + 4 \times \left( 12 \times 6 \right) \\
&= 144 + 4 \times \left( 72 \right) \\
&= 144 + 288 \\
&= 432
\end{align}$
Luas seluruh permukaan bangun adalah $240\ \text{cm}^{2} + 432\ \text{cm}^{2}=672\ \text{cm}^{2}$.
$\therefore$ Pilihan yang sesuai adalah $(B)\ 672\ \text{cm}^{2}$
69. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Aku adalah bangun ruang yang memiliki $5$ sisi, $9$ rusuk, dan $6$ titik sudut. Aku adalah...
Alternatif Pembahasan:
Dari informasi pada soal yang paling sesuai menggambarkan ciri dari prisma segitiga
$\therefore$ Pilihan yang sesuai adalah $(B)\ \text{prisma segitiga}$
70. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Jumlah panjang rusuk sebuah kubus adalah $96\ \text{cm}$. Luas permukaan kubus tersebut adalah...
Alternatif Pembahasan:
Kubus mempunyai rusuk yang sama sebanyak $12$ buah, sehingga saat panjang seluruh rusuknya $96\ \text{cm}$ maka panjang salah satu rusuknya adalah $\dfrac{96\ \text{cm}}{12}=8\ \text{cm}$.
Luas permukaan kubus terdiri dari $6$ persegi yang kongruen dimana panjang rusuknya adalah $8\ \text{cm}$, maka luas seluruh permukaan kubus adalah $6 \times 8\ \text{cm} \times 8\ \text{cm}=384\ \text{cm}^{2}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 384\ \text{cm}^{2}$
71. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Suatu balok memiliki luas permukaan $516\ \text{cm}^{2}$. Jika panjang dan lebar balok masing-masing $15\ \text{cm}$ dan $6\ \text{cm}$, maka tinggi balok tersebut adalah...
Alternatif Pembahasan:
Untuk luas permukaan balok $516\ \text{cm}^{2}$, $p=15\ \text{cm}$ dan $l=6\ \text{cm}$ maka dapat kita tentukan tingginya, yaitu:
$\begin{align}
L_{\text{balok}} &= 2 \times \left( p \times l + p \times t + l \times t \right) \\
516 &= 2 \times \left( 15 \times 6 + 15 \times t + 6 \times t \right) \\
258 &= 90 + 15t + 6t \\
168 &= 21t \\
t &= \dfrac{168}{21} = 8
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 8\ \text{cm}$
72. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Alas sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi $3\ \text{cm},$ $4\ \text{cm},$ dan $5\ \text{cm}$. Jika volume prisma adalah $36\ \text{cm}^{3}$, maka tinggi prisma tersebut adalah...
Alternatif Pembahasan:
Volume prisma adalah $\text{luas alas} \times \text{tinggi}$, untuk alas berupa segitiga siku-siku dengan panjang sisi $3\ \text{cm}$, $4\ \text{cm}$, $5\ \text{cm}$ dan ini merupakan tripel pythagoras maka dapat kita pastikan alas dan tinggi segitiga adalah $3\ \text{cm}$ dan $4\ \text{cm}$.
$\begin{align}
V\ &= L_{\text{segitiga}} \times \text{tinggi} \\
36\ \text{cm}^{3} &= \dfrac{1}{2} \times 3\ \text{cm} \times 4\ \text{cm} \times t \\
36\ \text{cm}^{3} &= 6t\ \text{cm}^{2} \\
t &= \dfrac{36\ \text{cm}^{3}}{6\ \text{cm}^{2}} \\
&= 6\ \text{cm}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 6\ \text{cm}$
73. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Perhatikan gambar berikut. Sebuah limas $T.ABCD$ tingginya $TP = 8\ \text{cm}$ dan tinggi rusuk tegaknya $TQ = 10\ \text{cm}$. Jika alasnya berbentuk persegi maka luas permukaan limas adalah...
Alternatif Pembahasan:
Luas permukaan limas segiempat adalah luas alas ditambah 4 luas segitiga.
Pada gambar di atas belum diketahui panjang rusuk persegi. Panjang rusuk persegi ini dapat kita ketahui dengan bantuan segitiga siku-siku $TPQ$ yaitu:
$\begin{align}
TQ^{2}\ &= TP^{2}+PQ^{2} \\
10^{2}\ &= 8^{2}+PQ^{2} \\
100\ &= 64+PQ^{2} \\
PQ^{2}\ &= 100-64 \\
PQ\ &= \sqrt{36}=6
\end{align}$
Untuk $PQ=6$ maka panjang rusuk persegi adalah $12$, sehingga luasnya adalah:
$\begin{align}
\left[ ABCD \right]\ &= AB \times CD \\
&= 12 \times 12 = 144
\end{align}$
Luas permukaan limas adalah:
$\begin{align}
L_{\text{Prisma}}\ &= \left[ ABCD \right] + 4 \times \left[ TBC \right] \\
&= 144 + 4 \times \dfrac{1}{2} \times 12 \times 10 \\
&= 144 + 240 = 384
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 384\ \text{cm}^{2}$
74. Contoh Soal PAS Matematika SMP/MTs |*Soal Lengkap
Volume balok yang berukuran $13\ \text{cm} \times 15\ \text{cm} \times 17\ \text{cm}$ adalah...
Alternatif Pembahasan:
Volume balok dengan ukuran $13\ \text{cm} \times 15\ \text{cm} \times 17\ \text{cm}$ adalah:
$\begin{align}
V_{\text{Balok}}\ &= 13\ \text{cm} \times 15\ \text{cm} \times 17\ \text{cm} \\
&= 3.315\ \text{cm}^{3}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 3.315\ \text{cm}^{3}$
75. Model Soal US-UM Matematika SMP 2023 |*Soal Lengkap
Perhatikan pernyataan berikut ini!Berdasarkan pernyataan di atas, sifat kubus ditunjukkan oleh pernyataan nomor...
- Rusuk kubus berukuran sama panjang
- Diagonal bidang/sisi sama panjang
- Sisi kubus berbentuk persegi panjang
- Diagonal bidang sama besar dengan diagonal ruang
Alternatif Pembahasan:
Pernyataan yang paling tepat untuk mewakili ciri-ciri kubus adalah pernyataan (1)Rusuk kubus berukuran sama panjang dan (2)Diagonal bidang/sisi sama panjang.
$\therefore$ Pilihan yang sesuai adalah $(A)\ 1\ \text{dan}\ 2$
Catatan Soal dan Pembahasan Bangun Ruang Sisi Datar dan Sisi Lengkung Matematika SMP di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.
Ayo Share (Berbagi) Satu Hal Baik.
Keberhasilan bukanlah milik orang yang pintar, tapi milik orang yang tekun dan tidak pernah menyerah.
