Pembahasan 30 Soal Sistem Persamaan Linear Dua Variabel (SPLDV) Matematika SMP

Calon guru belajar matematika dasar SMP lewat soal dan pembahasan bangun datar (segitiga dan segiempat) pada matematika SMP. Apa yang diharapkan setelah mempelajari materi ini, yaitu dengan aturan yang berlaku dan kreativitas berpikir kita dapat menyelesaikan masalah kontekstual yang berkaitan dengan luas dan keliling segiempat (persegi, persegipanjang, belahketupat, jajargenjang, trapesium, dan layang-layang) dan segitiga.

Soal matematika dasar segitiga dan segiempat untuk SMP ini kita pilih dari soal-soal yang sudah pernah diujikan pada soal Ujian Sekolah matematika SMP, soal Ujian Nasional matematika SMP, atau soal ujian seleksi akademik masuk SMA Unggulan atau SMA Plus.

---

SEGITIGA

Segitiga adalah poligon yang memiliki tiga sisi. Poligon diartikan dengan bangun datar yang terdiri dari garis lurus yang bergabung untuk membentuk rantai tertutup atau sirkuit.

---

SIFAT-SIFAT SEGITIGA

• Jumlah sudut bagian dalam segitiga adalah $180^{\circ}$.
• Jumlah panjang dua sisi pada segitiga harus lebih dari satu sisi segitiga yang lain.
• Sudut dalam terbesar menghadap sisi yang terpanjang dan aturan yang sama berlaku untuk sudut terkecil menghadap sisi yang terpendek.

---

Klasifikasi Segitiga Menurut Panjang Sisinya

• Segitiga sembarang: segitiga yang panjang sisinya tidak ada yang sama.
• Segitiga samakaki: segitiga yang memiliki dua panjang sisi yang sama
• Segitiga samasisi: segitiga yang memiliki tiga panjang sisi yang sama

---

Klasifikasi Segitiga Menurut Besar Sudutnya

• Segitiga lancip: segitiga yang ketiga sudutnya lebih kecil dari $90^{\circ}$ atau ketiga sudutnya merupakan sudut lancip.
• Segitiga siku-siku: segitiga yang salah satu sudutnya $90^{\circ}$
• Segitiga samasisi: segitiga yang ketiga sudutnya $60^{\circ}$
• Segitiga tumpul: segitiga yang salah satu sudutnya lebih dari $90^{\circ}$ atau salah satu sudutnya merupakan sudut tumpul.

---

LUAS DAN KELILING SEGITIGA

---

Garis Istimewa Pada Segitiga

• Garis Tinggi adalah garis dari titik sudut segitiga yang memotong salah satu sisi segitiga sehingga garis tegak lurus dengan sisi segitiga tersebut.
• Garis Berat adalah garis dari titik sudut segitiga yang memotong salah satu sisi segitiga sehingga garis membagi panjang sisi segitiga tersebut sama panjang.
• Garis Bagi adalah garis dari titik sudut segitiga yang memotong salah satu sisi segitiga sehingga garis membagi besar sudut segitiga tersebut sama besar.
• Garis Sumbu adalah garis yang tegak lurus dengan sisi segitiga dan membagi panjang sisi segitiga tersebut sama panjang.
Pada segitiga samasisi keempat garis di atas merupakan garis yang sama.

---

SEGIEMPAT

Segiempat adalah poligon yang memiliki empat sisi. Poligon diartikan dengan bangun datar yang terdiri dari garis lurus yang bergabung untuk membentuk rantai tertutup atau sirkuit.

Segiempat ada beberapa jenis yang sudah kita kenal, antara lain persegi, persegipanjang, belahketupat, jajargenjang, trapesium, dan layang-layang.

---

PERSEGI (BUJUR SANGKAR)

---

PERSEGI PANJANG

---

BELAH KETUPAT

---

LAYANG-LAYANG

---

JAJAR GENJANG

---

TRAPESIUM

---

Pembahasan Soal Bangun Datar (Segitiga dan Segiempat) Matematika SMP

---

Soal dan Pembahasan Bentuk Akar Matematika SMP

Soal-soal bangun datar (segitiga dan segiempat) matematika SMP berikut ini, silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan periksa jawaban. Jika hasilnya belum memuaskan silahkan dicoba lagi untuk tes ulang.

Ayo dicoba terlebih dahulu, Sebelum melihat pembahasan soal.
Tunjukkan Kemampuan Terbaikmu!

Nama Peserta :
Tanggal Tes :
Jumlah Soal :	55 soal

Petunjuk Pengerjaan Soal:
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.

1. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Perhatikan gambar.

Besar sudut $BAC$ adalah...

$(A)\ 24^{\circ} $

$(B)\ 28^{\circ} $

$(C)\ 55^{\circ} $

$(D)\ 65^{\circ} $

Alternatif Pembahasan:

Untuk setiap segitiga, jumlah sudut dalam segitiga adalah $180^{\circ}$, sehingga berlaku;
$\begin{align}
180 &= \angle ABC+\angle BCA+\angle BAC \\
180 &= 8x+1+4x+7+2x+4 \\
180 &= 14x+12 \\
180-12 &= 14x \\
\dfrac{168}{14} &= x \\
12 &=x
\end{align}$
Besar $\angle BAC=2x+4=2(12)+4=28$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 28^{\circ}$

2. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Sebuah taman berbentuk persegipanjang dengan panjang diagonal $(6x+4)$ meter dan $(7x-1)$ meter. Panjang diagonal taman tersebut adalah...

$(A)\ 5\ m $

$(B)\ 26\ m $

$(C)\ 34\ m $

$(D)\ 36\ m $

Alternatif Pembahasan:

Panjang diagonal sebuah persegi adalah sama, sehingga berlaku:
$\begin{align}
6x+4 &= 7x-1 \\
4+1 &= 7x-6x \\
5 &= x \\
\end{align}$
Panjang diagonal adalah $ 6x+4=6(5)+4=34$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 34\ m$

3. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Perhatikan gambar

Jika luas daerah yang tidak diarsir $55\ cm^{2}$, luas daerah yang diarsir adalah...

$(A)\ 5\ cm^{2} $

$(B)\ 10\ cm^{2} $

$(C)\ 20\ cm^{2} $

$(D)\ 40\ cm^{2} $

Alternatif Pembahasan:

Gambar di atas kita coba bagi menjadi tiga bagian yaitu, bagian $A$, $B$ dan $C$, seperti gambar berikut;

Luas daerah yang tidak diarsir $A+C=55$ dan luas daerah yang diarsir $B$, sehingga berlaku:
$\begin{align} [A+B ] &= \dfrac{1}{2} \cdot 10\ \cdot 7 \\ &= 35 \\
\hline
[B+C ] &= \dfrac{1}{2} \cdot 10\ \cdot 12 \\ &= 60 \\
\hline
[A+B+B+C ] &= 35+60 \\ [A+C ]+[2B ] &= 95 \\ 55+[2B ] &= 95 \\ [2B ] &= 95-55 \\ [2B ] &= 40 \\ [ B ] &= 20 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 20\ cm^{2}$

4. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap

Utari memiliki selembar karton untuk membuat namanya dengan huruf kapital. Ia memulai dengan huruf "U" seperti tampak pada gambar berikut.

Luas karton yang diperlukan untuk membuta huruf "U" tersebut adalah...

$(A)\ 228\ cm^{2} $

$(B)\ 168\ cm^{2} $

$(C)\ 120\ cm^{2} $

$(D)\ 100\ cm^{2} $

Alternatif Pembahasan:

Gambar kita berikan garis bantu, ilustrasinya seperti berikut:

Dari gambar diatas kita peroleh $3$ persegi panjang dimana $2$ persegi panjang adalah kongruen.

• Persegi panjang pertama luasnya adalah $5 \times 18 = 90$
• Persegi panjang kedua luasnya adalah $5 \times 18 = 90$
• Persegi panjang kedua luasnya adalah $8 \times 6 = 48$

Total luas karton adalah $90+90+48=228$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 228\ cm^{2}$

5. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap

Pada gambar berikut, panjang $FL=KD=12\ cm$, $FK=4\ cm$ dan $FM=DE=16\ cm$. Keliling bangun tersebut adalah...

$(A)\ 78\ cm $

$(B)\ 80\ cm $

$(C)\ 86\ cm $

$(D)\ 92\ cm $

Alternatif Pembahasan:

Dengan memperhatikan gambar, kita dapat dua segitiga siku-siku yaitu $EDK$ dan $FLM$, dimana sebagian sisi segitiga berimpit.
Keliling bagun datar adalah: $16+8+20+12+4+20=80$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 80\ cm$

6. Soal UNBK Matematika SMP 2018 |*Soal Lengkap

Andi akan membuat huruf L seperti gambar!

Luas karton yang dibutuhkan adalah...

$(A)\ 30\ cm^{2} $

$(B)\ 20\ cm^{2} $

$(C)\ 18\ cm^{2} $

$(D)\ 10\ cm^{2} $

Alternatif Pembahasan:

Gambar kita berikan garis bantu, ilustrasinya seperti berikut:

Dari gambar kita peroleh $2$ persegi panjang;
Persegi panjang pertama luasnya adalah $4 \times 2 = 8$
Persegi panjang kedua luasnya adalah $5 \times 2 = 10$

$\therefore$ Luas karton yang dibutuhkan adalah $(B)\ 18\ cm^{2}$

7. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar berikut!

Sebidang tanah berbentuk trapesium samakaki. Di bagian dalam akan dibuat kolam ikan yang sebangun dengan tanah tersebut. Di sekeliling kolam dibangun jalan setapak. Luas jalan tersebut adalah...

$(A)\ 216\ m^{2} $

$(B)\ 226\ m^{2} $

$(C)\ 236\ m^{2} $

$(D)\ 316\ m^{2} $

Alternatif Pembahasan:

Untuk menghitung luas jalan, kita coba hitung dari luas tanah dan luas kolam. Bentuk tanah dan kolam sama-sama berbentuk trapesium sama kaki sehingga kedua trapesium adalah trapesium yang sebangun. Sehingga berlaku:
$\begin{align} \dfrac{x}{15} &=\dfrac{36}{y} =\dfrac{20}{25} \\ \dfrac{x}{15} &=\dfrac{36}{y} =\dfrac{4}{5} \\ \hline \dfrac{x}{15} &=\dfrac{4}{5} \\ x &= \dfrac{4}{5} \times 15 \\ x &=12 \\ \hline \dfrac{36}{y} &= \dfrac{4}{5} \\ y &= \dfrac{5}{4} \times 36 \\ y &= 45 \end{align}$

Untuk mendapatkan luas jalan, kita bisa dapat dari selisih luas tanah dengan luas kolam.

Dengan memperhatikan data-data pada gambar dapat kita peroleh:

• Luas Tanah
  $\begin{align}
  L_{t}\ &= \dfrac{1}{2} \times (15+45) \times 20 \\ &= \dfrac{1}{2} \times 60 \times 20 \\ &= 600\ m^{2} \end{align}$
• Luas Kolam
  $\begin{align}
  L_{k}\ &= \dfrac{1}{2} \times (12+36) \times 16 \\ &= \dfrac{1}{2} \times 48 \times 16 \\ &= 384\ m^{2} \end{align}$
• Luas jalan adalah selisih luas tanah dengan luas kolam yaitu:
  $\begin{align}
  L_{j}\ &= L_{t}-L_{k} \\ &= 600\ m^{2} - 384\ m^{2}\\ &= 216\ m^{2} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 216\ m^{2}$

8. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

Tanah pekarangan pak Ahsan berbentuk persegipanjang dengan panjang $24$ meter dan lebar $18$ meter. Di sekeliling tanah tersebut dipasang kawat sebagai pagar sebanyak $3$ lapis. Panjang kawat yang diperlukan adalah...

$(A)\ 432\ \text{meter} $

$(B)\ 360\ \text{meter} $

$(C)\ 252\ \text{meter} $

$(D)\ 162\ \text{meter} $

Alternatif Pembahasan:

Tanah yang dimiliki pak Ahsan berbentuk persegi panjang denga ukuran $p=24$ dan $l=18$.
Panjang kawat yang dibutuhkan untuk mengelilingi tanah tersebut satu kali adalah menggunakan konsep keliling persegi panjang, yaitu:
$k=2p+2l$
$k=2(24)+2(18)$
$k=48+36$
$k=84$
Karena kawat mengelilingi tanah sebanyak $3$ kali, maka panjang kawat yang dibutuhkan adalah $3 \times 84=252$ meter.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 252\ \text{meter}$

9. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar berikut!

Luas daerah yang diarsir adalah...

$(A)\ 136\ m^{2} $

$(B)\ 163\ m^{2} $

$(C)\ 200\ m^{2} $

$(D)\ 236\ m^{2} $

Alternatif Pembahasan:

Luas daerah yang diarsir kita tentukan dari $\left[ ABE \right]$ dan $\left[ BED \right]$, dapat kita peroleh:
$\begin{align} [ ABE ] &= [ ABC ] + [ BCE ] \\ \dfrac{1}{2} \cdot 16\ \cdot 10 &= [ ABC ] + \dfrac{1}{2} \cdot 16\ \cdot 4 \\ 80 &= [ ABC ] + 32 \\ 48 &= [ ABC ] \\ \hline [ BED ] &= [ CDE ] + [ BCE ] \\ \dfrac{1}{2} \cdot 16\ \cdot 15 &= [ CDE ] + \dfrac{1}{2} \cdot 16\ \cdot 4 \\ 120 &= [ CDE ] + 32 \\ 88 &= [ CDE ] \\ \hline L_{\text{arsir}} &= [ ABC ] + [ CDE ] \\ &= 48 + 88 \\ &= 136 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 136\ cm^{2}$

10. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

Diketahui segitiga dengan panjang sisi $a,\ b,$ dan $c$, dengan syarat $a \gt b \gt c$. Pernyataan yang benar sesuai dengan konsep segitiga adalah...

$(A)\ b+c \gt a $

$(B)\ a+c \lt b $

$(C)\ a+b \lt c $

$(D)\ a+b = c $

Alternatif Pembahasan:

Panjang sisi pada segitiga konsepnya memenuhi aturan "Jumlah dua panjang sisi segitiga harus lebih panjang dari sisi yang lain".
Secara simbolik dapat kita tuliskan, jika $a,\ b,\ c$ adalah panjang sisi-sisi segitiga maka berlaku:

• $a+b \gt c$,
• $a+c \gt b$, dan
• $b+c \gt a$

$\therefore$ Pilihan yang sesuai adalah $(A)\ b+c \gt a$

11. Soal Masuk YASOP - SMAN 2 Balige 2018 |*Soal Lengkap

Pasangan ruas garis berikut yang dapat membentuk segitiga adalah segitiga dengan panjang sisi...

$(A)\ 7,4,12 $

$(B)\ 10,6,20 $

$(C)\ 7,11,19 $

$(D)\ 21,11,12 $

Alternatif Pembahasan:

Sebuah segitiga dapat dibangun oleh tiga buah ruas garis dengan syarat "jumlah panjang dua garis harus lebih dari garis yang lain"

• $7,4,12$ tidak memenuhi karena $7+4 \lt 12$
• $10,6,20$ tidak memenuhi karena $10+6 \lt 20$
• $7,11,19$ tidak memenuhi karena $7+11 \lt 19$
• $21,11,12$ memenuhi karena:
  
  • $21+11 \gt 12$
  • $21+12 \gt 11$
  • $11+12 \gt 21$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 21,11,12$

12. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

Nilai $a,b$ dan $c$ adalah sisi-sisi sebuah segitiga, jika $a$ sisi terpanjang, maka pernyataan berikut yang selalu benar adalah...

$(A)\ a \gt b+c $

$(B)\ a \lt b+c $

$(C)\ a \leq b+c $

$(D)\ a^{2}+b^{2}=c^{2} $

Alternatif Pembahasan:

Untuk setiap segitiga $ABC$, jika $a,b,c$ adalah panjang sisi-sisi segitiga maka berlaku $a+b \gt c$, $a+c \gt b$ dan $b+c \gt a$.

$\therefore$ Pilihan yang sesuai adalah $(A)\ b+c \gt a $

13. Soal Masuk YASOP - SMAN 2 Balige 2007 |*Soal Lengkap

Perhatikan gambar di bawah ini!

Diketahui persegi $ABCD$ dan persegipanjang $PQRS$. Jika keliling persegi panjang sama dengan dua kali keliling persegi, maka panjang sisi persegi adalah...

$(A)\ 12\ cm $

$(B)\ 9\ cm $

$(C)\ 8\ cm $

$(D)\ 6\ cm $

Alternatif Pembahasan:

Kita misalkan panjang sisi persegi $ABCD$ adalah $x$ sehingga kelilingnya adalah $4x$.

Keliling $PQRS$ adalah $2 \times 9+2 \times 15=48$

Jika keliling persegi panjang sama dengan dua kali keliling persegi, maka
$\begin{align}
2(4x) & = 48 \\ 8x & = 48 \\ x & = \dfrac{48}{8} \\ x & = 6
\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 6\ cm$

14. Soal UN Matematika SMP 2015 |*Soal Lengkap

Perhatikan gambar!

Garis $CE$ adalah...

$(A)\ \text{Garis Berat} $

$(B)\ \text{Garis Bagi} $

$(C)\ \text{Garis Tinggi} $

$(D)\ \text{Garis Sumbu} $

Alternatif Pembahasan:

Pada segitiga ada empat garis khusus yaitu:

• Garis Tinggi adalah garis dari titik sudut segitiga yang memotong salah satu sisi segitiga sehingga garis tegak lurus dengan sisi segitiga tersebut.
• Garis Berat adalah garis dari titik sudut segitiga yang memotong salah satu sisi segitiga sehingga garis membagi panjang sisi segitiga tersebut sama panjang.
• Garis Bagi adalah garis dari titik sudut segitiga yang memotong salah satu sisi segitiga sehingga garis membagi besar sudut segitiga tersebut sama besar.
• Garis Sumbu adalah garis yang tegak lurus dengan sisi segitiga dan membagi panjang sisi segitiga tersebut sama panjang.
Pada segitiga samasisi keempat garis di atas merupakan garis yang sama.

$\therefore$ Pilihan yang sesuai adalah $(A)\ \text{Garis Berat}$

15. Soal UN Matematika SMP 2010 |*Soal Lengkap

Perhatikan gambar belahketupat $ABCD$

$\angle A : \angle B = 1 : 2$. Besar $\angle C$ adalah...

$(A)\ 60^{\circ} $

$(B)\ 90^{\circ} $

$(C)\ 120^{\circ} $

$(D)\ 150^{\circ} $

Alternatif Pembahasan:

Perbandingan $\angle A : \angle B = 1 : 2$ dapat kita misalkan menjadi $\angle A : \angle B = 1x : 2x$ sehingga $\angle A=1x$ dan $\angle B = 2x$.

Berdasarkan ciri belahketupat, sudut yang sehadap sama besar dan jumlah keempat sudut adalah $360^{\circ}$, sehingga kita peroleh:
$\begin{align}
\angle A+\angle B +\angle C+ \angle D &= 360^{\circ} \\ 1x+ 2x + 1x + 2x &= 360^{\circ} \\ 6x &= 360^{\circ} \\ x &= \dfrac{360^{\circ}}{6} \\ &= 60^{\circ} \\ \hline \angle C &= x \\ &=60^{\circ} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 60^{\circ}$

16. Soal UN Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar!

Luas karton yang digunakan untuk membuat bangun huruf $E$ adalah...

$(A)\ 1.448\ cm^{2} $

$(B)\ 1.356\ cm^{2} $

$(C)\ 1.224\ cm^{2} $

$(D)\ 924\ cm^{2} $

Alternatif Pembahasan:

Dari informasi pada soal kita peroleh:

$\therefore$ Pilihan yang sesuai adalah $(C)\ 1.224\ cm^{2}$

17. Soal UN Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar bangun yang terdiri dari jajargenjang dan segitiga siku-siku.

Keliling bangun tersebut adalah...

$(A)\ 105\ cm $

$(B)\ 120\ cm $

$(C)\ 123\ cm $

$(D)\ 156\ cm $

Alternatif Pembahasan:

Dari informasi pada soal dapat kita peroleh:

$\therefore$ Pilihan yang sesuai adalah $(B)\ 120\ cm$

18. Soal UN Matematika SMP 2018 |*Soal Lengkap

Ruangan sebuah aula dengan panjang $21\ m$ dan lebar $15\ m$ akan ditutupi dengan ubin berukuran $30\ cm \times 30\ cm$. Banyaknya ubin yang diperlukan untuk menutup semua lantai aula adalah...

$(A)\ 35.000\ \text{ubin} $

$(B)\ 3.500\ \text{ubin} $

$(C)\ 350\ \text{ubin} $

$(D)\ 35\ \text{ubin} $

Alternatif Pembahasan:

Luas ruangan sebuah aula dengan panjang $21\ m=2.100\ cm$ dan lebar $15\ m=1.500\ cm$ adalah:
$\begin{align}
L_{\text{aula}} &= p \times l \\ &= 2.100\ cm \times 1.500\ cm \\ &= 3.150.000\ cm^{2} \end{align}$

Luas ubin dengan panjang $30\ cm$ dan lebar $30\ cm$ adalah:
$\begin{align}
L_{\text{ubin}} &= p \times l \\ &= 30\ cm \times 30\ cm \\ &= 900\ cm^{2} \end{align}$

Banyak ubin yang diperlukan adalah $3.150.000 \ cm^{2}$ dibagi $900\ cm^{2}$ yaitu $3.500$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 3.500\ \text{ubin}$

19. Soal UN Matematika SMP 2016 |*Soal Lengkap

Perhatikan gambar berikut!

Luas daerah yang diarsir adalah...

$(A)\ 45\ m^{2} $

$(B)\ 54\ m^{2} $

$(C)\ 72\ m^{2} $

$(D)\ 81\ m^{2} $

Alternatif Pembahasan:

Luas daerah yang diarsir kita tentukan dari $\left[ ADB \right]$ dan $\left[ ADE \right]$, dapat kita peroleh:
$\begin{align} [ ADB ] &= [ ADC ] + [ ABC ] \\ \dfrac{1}{2} \cdot 9\ \cdot 8 &= \dfrac{1}{2} \cdot 9\ \cdot 2 + [ ABC ] \\ 36 &= 9 + [ ABC ] \\ 27 &= [ ABC ] \\ \hline [ ADE ] &= [ ADC ] + [ CDE ] \\ \dfrac{1}{2} \cdot 9\ \cdot 12 &= \dfrac{1}{2} \cdot 9\ \cdot 2 + [ CDE ] \\ 54 &= [ CDE ] + 9 \\ 45 &= [ CDE ] \\ \hline L_{\text{arsir}} &= [ ABC ] + [ CDE ] \\ &= 27 + 45 \\ &= 72 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 72\ cm^{2}$

20. Soal UN Matematika SMP 2018 |*Soal Lengkap

Nabil mempunyai sebidang tanah berbentuk persegipanjang berukuran $70\ m \times 30\ m$. Di sekeliling tanah dipagari dengan biaya per meter $Rp30.000,00$ biaya pemagaran seluruhnya adalah...

$(A)\ Rp63.000.000,00 $

$(B)\ Rp36.000.000,00 $

$(C)\ Rp6.000.000,00 $

$(D)\ Rp3.000.000,00 $

Alternatif Pembahasan:

Keliling tanah berbentuk persegipanjang berukuran $70\ m \times 30\ m$ adalah:
$\begin{align}
K_{\text{tanah}} &= 2 \left( p + l \right) \\ &= 2 \left( 70\ m+30\ m \right) \\ &= 200\ m \end{align}$

Biaya pagar keseluruhn adalah:
$\begin{align}
B_{\text{pagar}} &= 200 \times Rp30.000,00 \\ &= Rp6.000.000,00\ m \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ Rp6.000.000,00\ m$

21. Soal UN Matematika SMP 2018 |*Soal Lengkap

keliling suatu persegi panjang $80\ cm$. Jika perbandingan panjang dan lebarnya $7 : 3$, maka luas persegi panjang tersebut adalah...

$(A)\ 336\ cm^{2} $

$(B)\ 320\ cm^{2} $

$(C)\ 268\ cm^{2} $

$(D)\ 210\ cm^{2} $

Alternatif Pembahasan:

Perbandingan panjang dan lebar persegipanjang $7 : 3$, ini dapat kita tuliskan menjadi $7a : 3a$ sehingga $p=7a$ dan $l=3a$. Untuk keliling $80\ cm$, kita peroleh:
$\begin{align}
K_{\text{tanah}} &= 2 \left( p + l \right) \\ 80 &= 2 \left( 7a + 3a \right) \\ 80 &= 20a\ longrightarrow a=4 \end{align}$

Untuk $a=4$ kita peroleh $p=7a=28$ dan $l=3a=12$, sehingga luas persegipanjang adalah:
$\begin{align}
L &= p \times l \\ &= 28\ cm \times 12\ cm \\ &= 336\ cm^{2} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 336\ cm^{2}$

22. Soal UN Matematika SMP 2015 |*Soal Lengkap

Perhatikan gambar!

Jika panjang $OC=6\ cm$, maka luas bangun $ABCDEF$ adalah...

$(A)\ 636\ cm^{2} $

$(B)\ 468\ cm^{2} $

$(C)\ 418\ cm^{2} $

$(D)\ 318\ cm^{2} $

Alternatif Pembahasan:

Dari informasi pada soal, dapat kita ketahui bangun $ABCDEF$ adalah bangun layang-layang dan jajar genjang.

Dari layang-layang $BCDE$, segitiga $OCD$ dan segitiga $ODE$ adalah segitiga siku-siku sehingga berlaku:
$\begin{align} CD^{2} &= OC^{2} + OD^{2} \\ 10^{2} &= 6^{2} + OD^{2} \\ 100 &= 36 + OD^{2} \\ OD^{2} &= 100-36 \\ OD &= \sqrt{64}=8 \\ \hline DE^{2} &= OD^{2} + OE^{2} \\ 17^{2} &= 8^{2} + OE^{2} \\ 289 &= 64 + OE^{2} \\ OE^{2} &= 225 \\ OD &= \sqrt{225}=15 \\ \hline [BCDE] &= \dfrac{1}{2} \times BD \times CE \\ &= \dfrac{1}{2} \times (2 \cdot OD) \times (OE + OC) \\ &= \dfrac{1}{2} \times (16) \times (21) \\ &= 168 \end{align}$

Luas $ABCDEF$ adalah:
$\begin{align} [ABEF] + [BCDE] &= [ABEF] + [BCDE] \\ &= AB \times OE + 168 \\ &= 20 \times 15 + 168 \\ &= 300 + 168 =468 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 468\ cm^{2}$

23. Soal UN Matematika SMP 2015 |*Soal Lengkap

Sebuah kolam renang berbentuk persegi panjang berukuran $15\ m$ dan $10\ m$. Di sekeliling kolam dibuat jalan dengan lebar $1\ m$ dan dipasang keramik. Luas keramik yang diperlukan untuk jalan adalah...

$(A)\ 45\ m^{2} $

$(B)\ 46\ m^{2} $

$(C)\ 50\ m^{2} $

$(D)\ 54\ m^{2} $

Alternatif Pembahasan:

Dari informasi pada soal, jika kita gambarkan keadaan kolam dan jalan, dapat seperti berikut ini:

Dari gambar di atas luas keramik yang dibutuhkan sama dengan luas jalan, yang dapat kita peroleh dari selisih luas tanah dan luas kolam yaitu:
$\begin{align} L_{\text{Jalan}} &= L_{\text{Tanah}}-L_{\text{Kolam}} \\ &= 15 \times 10 - 13 \times 8 \\ &= 150 - 104 \\ &= 46 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 46\ m^{2}$

24. Soal UN Matematika SMP 2015 |*Soal Lengkap

Sebuah taman berbentuk persegi panjang berukuran panjang $32\ m$ dan lebar $24\ m$. Di sekeliling taman akan dipasang lampu dengan jarak antar lampu $4\ m$. Jumlah lampu yang diperlukan...

$(A)\ 14\ \text{lampu} $

$(B)\ 28\ \text{lampu} $

$(C)\ 52\ \text{lampu} $

$(D)\ 112\ \text{lampu} $

Alternatif Pembahasan:

Dari informasi pada soal di sekeliling taman akan dipasang lampu dengan jarak antar lampu $4\ m$. Sehingga kita perlu panjang keliling taman yaitu:
$\begin{align} K_{\text{Taman}} &= 2 \left( p+ l \right) \\ &= 2 \left( 32+ 24 \right) \\ &= 112 \\ \hline B_{\text{lampu}} &= \dfrac{112}{4}=28 \end{align}$

Jika kita gambarkan keadaan taman dan lampu, dapat seperti berikut ini:

$\therefore$ Pilihan yang sesuai adalah $(B)\ 28\ \text{lampu}$

25. Soal UN Matematika SMP 2014 |*Soal Lengkap

Diketahui keliling persegipanjang $64\ m$ dengan ukuran panjang $\left( 3x+7 \right)\ cm$ dan lebar $\left( 2x+5 \right)\ cm$, maka panjang dan lebar persegi panajang berturut-turut adalah...

$(A)\ 26\ cm\ \text{dan}\ 6\ cm$

$(B)\ 22\ cm\ \text{dan}\ 10\ cm$

$(C)\ 19\ cm\ \text{dan}\ 13\ cm$

$(D)\ 18\ cm\ \text{dan}\ 14\ cm $

Alternatif Pembahasan:

Dari informasi pada soal keliling persegipanjang $64\ m$, sehingga dapat kita peroleh:
$\begin{align} K_{\text{Taman}} &= 2 \left( p+ l \right) \\ 64 &= 2 \left( 3x+7+ 2x+5 \right) \\ 64 &= 2 \left( 5x+12 \right) \\ 64 &= 10x + 24 \\ 64-24 &= 10x \\ 40 &= 10x \longrightarrow x=\dfrac{40}{10}=4 \\ \hline p &= 3x+7=3(4)+7=19 \\ l &= 2x+5=2(4)+5=13 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 19\ cm\ \text{dan}\ 13\ cm$

26. Soal UN Matematika SMP 2014 |*Soal Lengkap

Perhatikan gambar!

$ABCD$ dan $EFGH$ adalah persegi, titik $D$ dalah titik pusat persegi $EFGH$. Luas daerah yang diarsir adalah...

$(A)\ 32\ cm^{2} $

$(B)\ 24\ cm^{2} $

$(C)\ 16\ cm^{2} $

$(D)\ 12\ cm^{2} $

Alternatif Pembahasan:

Dari informasi pada soal, dapat kita gambarkan dua buah segitiga yang kongruen pada persegi $EFGH$ seperti gambar berikut ini:

$\therefore$ Pilihan yang sesuai adalah $(C)\ 16\ cm^{2}$

27. Soal UN Matematika SMP 2014 |*Soal Lengkap

Perhatikan gambar berikut ini!

Keliling bangun tersebut adalah...

$(A)\ 61\ cm $

$(B)\ 84\ cm $

$(C)\ 90\ cm $

$(D)\ 94\ cm $

Alternatif Pembahasan:

Dari informasi pada soal, gambar pada soal dapat kita gambarkan menjadi seperti berikut ini:

Dari gambar di atas kita peroleh keliling bangun adalah:
$\begin{align} K &= P_{merah} + P_{biru}+P_{hijau} \\ &= 2 \times 18 + 2 \times 20 + 2 \times 4 \\ &= 36 + 40+8 \\ &= 84 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 84\ cm$

28. Soal UN Matematika SMP 2013 |*Soal Lengkap

Sebuah belah ketupat $KLMN$ dengan diagonal $KM=24\ cm$. Jika luas belahketupat $384\ cm^{2}$, keliling belahketupat tersebut adalah...

$(A)\ 16\ cm $

$(B)\ 20\ cm $

$(C)\ 32\ cm $

$(D)\ 80\ cm $

Alternatif Pembahasan:

Dari informasi pada soal, belah ketupat dapat kita gambarkan menjadi seperti berikut ini:

$\therefore$ Pilihan yang sesuai adalah $(D)\ 80\ cm$

29. Soal UN Matematika SMP 2013 |*Soal Lengkap

Perhatikan gambar persegipanjang $KLMN$ dan persegi $PQRS$!

Jika luas daerah yang diarsir $40\ cm^{2}$, luas daerah yang tidak diarsir adalah...

$(A)\ 80\ cm^{2} $

$(B)\ 176\ cm^{2} $

$(C)\ 216\ cm^{2} $

$(D)\ 256\ cm^{2} $

Alternatif Pembahasan:

Gambar di atas kita coba bagi menjadi tiga bagian yaitu, bagian $[A]$, $[B]$ dan $40$, seperti gambar berikut;

Luas daerah yang diarsir kita tentukan dari $\left[ PQRS \right]$ dan $\left[ KLMN \right]$, dapat kita peroleh:
$\begin{align} [ KLMN ] &= [ B ] + 40 \\ 16\ \cdot 12 &=[ B ] + 40 \\ 192 &= [ B ] + 40 \\ 152 &= [ B ] \\ \hline [ PQRS ] &= [ A ] + 40 \\ 8\ \cdot 8 &= [ A ] + 40 \\ 64 &= [ A ] + 40 \\ 24 &= [ A ] \\ \hline L_{\text{tidak diarsir}} &= [A] + [B] \\ &= 152 + 24 \\ &= 176 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 176\ cm^{2} $

30. Soal UN Matematika SMP 2013 |*Soal Lengkap

Sebuah taman berbentuk persegi, di sekelilingnya akan dipasang lampu dengan jarak antar lampu $6$ meter. Jika panjang sisi taman $30$ meter, banyak lampu yang dipasang adalah...

$(A)\ 5\ \text{lampu} $

$(B)\ 10\ \text{lampu} $

$(C)\ 15\ \text{lampu} $

$(D)\ 20\ \text{lampu} $

Alternatif Pembahasan:

Dari informasi pada soal di sekeliling taman akan dipasang lampu dengan jarak antar lampu $6\ m$. Sehingga kita perlu panjang keliling taman yaitu:
$\begin{align} K_{\text{Taman}} &= 4p \\ &= 4 \times 30\ m \\ &= 120\ m \\ \hline B_{\text{lampu}} &= \dfrac{120\ m}{6\ m}=20 \end{align}$

Jika kita gambarkan keadaan taman dan lampu, dapat seperti berikut ini:

$\therefore$ Pilihan yang sesuai adalah $(D)\ 20\ \text{lampu}$

31. Soal UN Matematika SMP 2012 |*Soal Lengkap

Luas belahketupat yang panjang salah satu diagonalnya $10\ cm$ dan kelilingnya $52\ cm$ adalah...

$(A)\ 120\ cm^{2} $

$(B)\ 130\ cm^{2} $

$(C)\ 240\ cm^{2} $

$(D)\ 260\ cm^{2} $

Alternatif Pembahasan:

Dari informasi pada soal, belah ketupat dapat kita gambarkan menjadi seperti berikut ini:

Dari apa yang sudah didapat pada gambar di atas, dapat kita peroleh:
$\begin{align} \text{Luas} & = \dfrac{1}{2} \times AC \times BD \\ & = \dfrac{1}{2} \times 10 \times 24 \\ & = 120 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 120\ cm^{2}$

32. Soal UN Matematika SMP 2012 |*Soal Lengkap

Perhatikan gambar persegi $PQRS$ dengan $PQ=12\ cm$ dan persegipanjang $ABCD$ dengan $DC=15\ cm$; $AD=6\ cm$. Luas daerah yang tidak di arsir $198\ cm^{2}$, luas daerah yang diarsir adalah...

$(A)\ 18\ cm^{2} $

$(B)\ 36\ cm^{2} $

$(C)\ 54\ cm^{2} $

$(D)\ 72\ cm^{2} $

Alternatif Pembahasan:

Gambar di atas kita coba bagi menjadi tiga bagian yaitu, bagian $[X]$, $[Y]$ dan $[Z]$, seperti gambar berikut;

Luas daerah yang diarsir kita tentukan dari $\left[ ABCD \right]$ dan $\left[ PQRS \right]$, dapat kita peroleh:
$\begin{align} [ X ] + [Z] &= 198 \\ \hline [ ABCD ]+[ PQRS ] &= [ X ] + [ Y ] + [ Y ] + [ Z ] \\ 90+ 144 &= [ X ] + [ Z ] + 2[ Y ] \\ 234 &= 198 + 2[ Y ] \\ 234-198 &= 2[ Y ] \\ 36 &= 2[ Y ] \\ 18 &= [Y] \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 18\ cm^{2} $

33. Soal UN Matematika SMP 2012 |*Soal Lengkap

Di atas sebidang tanah berbentuk persegipanjang dengan ukuran $12\ m \times 6\ m$ akan dibuat pagar di sekelilingnya. Untuk kekuatan pagar, setiap jarak $3\ m$ ditanam tiang pancang. Banyak tiang pancang yang ditanam adalah...

$(A)\ 12 $

$(B)\ 13 $

$(C)\ 14 $

$(D)\ 15 $

Alternatif Pembahasan:

Dari informasi pada soal di sekeliling tanah akan dipasang tiang pancang dengan jarak $3\ m$. Sehingga kita perlu panjang keliling tanah yaitu:
$\begin{align} K_{\text{Tanah}} &= 2 \left( p+ l \right) \\ &= 2 \left( 15+ 6 \right) \\ &= 2 \left( 21 \right) \\ &= 42 \\ \hline B_{\text{pancang}} &= \dfrac{42}{3}=14 \end{align}$

Jika kita gambarkan keadaan tanah dan pancang, dapat seperti berikut ini:

$\therefore$ Pilihan yang sesuai adalah $(C)\ 14$

34. Soal UN Matematika SMP 2011 |*Soal Lengkap

Perhatikan bangun trapesium $ABCF$ dan layang-layang $EFCD$. Jika panjang $CE=21\ cm$, keliling bangun tersebut adalah...

$(A)\ 105\ cm $

$(B)\ 97\ cm $

$(C)\ 88\ cm $

$(D)\ 80\ cm $

Alternatif Pembahasan:

Dari informasi pada soal, Bangun $ABCDEF$ adalah bangun layang-layang dan trapesium. Jika titik potong diagonal layang-layang kita misalkan dengan $O$ maka dapat kita gambarkan menjadi seperti berikut ini:

Dari gambar di atas kita peroleh $OA=BC$ sehingga $OF=22-14=8$ dan $OD=8$. Untuk $OD=8$ dari segitiga siku-siku $OCD$ kita peroleh:
$\begin{align} CD^{2} &= OC^{2} + OD^{2} \\ 17^{2} &= OC^{2} + 8^{2} \\ 289 &= OC^{2}+64 \\ OC^{2} &= 289-64 \\ OC &= \sqrt{225}=15 \longrightarrow AB=15 \\ \hline DE^{2} &= OD^{2} + OE^{2} \\ DE^{2} &= 8^{2} + 6^{2} \\ DE^{2} &= 64 + 36 \\ DE^{2} &= 100 \\ DE &= \sqrt{100}=10 \\ \hline K &= AB+BC+CD+DE+EF+FA \\ K &= 15+22+17+10+10+14 \\ &= 88 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 88\ cm^{2}$

35. Soal UN Matematika SMP 2011 |*Soal Lengkap

Pak Ali mempunyai kebun dengan bentuk seperti pada gambar. Kebun tersebut akan dijual dengan harga $Rp200.000,00$ per $m^{2}$. Hasil penjualan kebun Pak Ali adalah...

$(A)\ Rp28.800.000,00 $

$(B)\ Rp30.000.000,00 $

$(C)\ Rp36.000.000,00 $

$(D)\ Rp57.600.000,00 $

Alternatif Pembahasan:

Dari gambar di atas kita peroleh $ADEF$ adalah sebuah jajargenjang dengan tinggi $10$, $AD=FE=12$ dan $AB=BD=6$. Kita peroleh luas $ADEF$ adalah:
$\begin{align} [ADEF] &= AD \times 10 \\ [ADEF] &= 12 \times 10 \\ &= 120\ m^{2} \end{align}$

Dari gambar di atas juga kita peroleh $BCD$ adalah sebuah segitiga siku-siku tinggi $BC=10$ dan alas $BD=6$. Kita peroleh luas $BCD$ adalah:
$\begin{align} [BCD] &= \dfrac{1}{2} \times BD \times BC \\ [BCD] &= \dfrac{1}{2} \times 6 \times 10 \\ &= 30\ m^{2} \end{align}$

Luas total kebun adalah $120\ m^{2}+30\ m^{2}=150\ m^{2}$ sehingga untuk harga $Rp200.000,00$ per $m^{2}$ hasil penjualan adalah $150 \times Rp200.000,00 = Rp30.000.000,00$.

$\therefore$ Pilihan yang sesuai adalah $(B)\ Rp30.000.000,00$

36. Soal UN Matematika SMP 2011 |*Soal Lengkap

Perhatikan gambar!
Luas daerah yang diarsir adalah...

$(A)\ 276\ cm^{2} $

$(B)\ 264\ cm^{2} $

$(C)\ 246\ cm^{2} $

$(D)\ 228\ cm^{2} $

Alternatif Pembahasan:

Berdasarakan informasi pada soal, jika di gambar kita beri beberapa tambahan titik, maka kita peroleh gambar seperti berikut ini:

Dari gambar di atas kita peroleh $CDEF$ adalah sebuah persegi dan dengan panjang sisi $10$, sehingga luasnya adalah:
$\begin{align} [CDEF] &= 10 \times 10 \\ [CDEF] &= 100 \end{align}$

Dari gambar di atas juga kita peroleh $ABCF$ adalah sebuah trapesium, luas $ABCF$ adalah:
$\begin{align} BC^{2} &= 6^{2} + t^{2} \\ 10^{2} &= 36 + t^{2} \\ t^{2} &= 100-36 \\ t &= \sqrt{64}=8 \\ \hline [ABCF] &= \dfrac{1}{2} \times \left(AB + ED \right) \times t \\ &= \dfrac{1}{2} \times \left( 22 + 10 \right) \times 8 \\ &= 32 \times 4 = 128 \end{align}$

Luas total daerah yang diarsir adalah $100\ cm^{2}+120\ cm^{2}=228\ cm^{2}$.

$\therefore$ Pilihan yang sesuai adalah $(D)\ 228\ cm^{2}$

37. Soal UN Matematika SMP 2010 |*Soal Lengkap

Perhatikan gambar!
Luas daerah yang diarsir adalah sketsa tanah yang ditanami rumput.

Luas hamparan rumput tersebut adalah...

$(A)\ 954\ cm^{2} $

$(B)\ 904\ cm^{2} $

$(C)\ 454\ cm^{2} $

$(D)\ 404\ cm^{2} $

Alternatif Pembahasan:

Berdasarakan informasi pada soal, jika di gambar kita beri beberapa tambahan titik, maka kita peroleh gambar seperti berikut ini:

Dari gambar di atas dapat kita peroleh panjang $y$ dengan menggunakan teorema pythagoras, yaitu:
$\begin{align} 25^{2} &= 20^{2} + y^{2} \\ 625 &= 400 + y^{2} \\ y^{2} &= 625-400 \\ y &= \sqrt{225}=15 \end{align}$

Untuk $y=15$ maka dapat kita peroleh nilai $x$ yaitu:
$\begin{align} x+12 +x + y &= 35 \\ 2x+12 +15 &= 35 \\ 2x &= 35-27 \\ 2x &= 8\ \longrightarrow x=4 \end{align}$

Untuk $x=4$ maka luas total daerah hamparan rumput adalah:
$\begin{align} L &= (20)(x)+(12)(12)+(20)(x)+\dfrac{1}{2}(20)(y) \\ &= (20)(4)+(12)(12)+(20)(4)+\dfrac{1}{2}(20)(15) \\ &= 80+ 144+80+ 150 \\ &= 454 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 454\ cm^{2}$

38. Soal UN Matematika SMP 2010 |*Soal Lengkap

Perhatikan gambar berikut!

Keliling daerah yang diarsir adalah....

$(A)\ 46\ cm $

$(B)\ 96\ cm $

$(C)\ 116\ cm $

$(D)\ 126\ cm $

Alternatif Pembahasan:

Berdasarakan informasi pada soal, untuk menghitung keliling daerah yang diarsir kita perlu ketahui panjang $PQ=PS=SR$ yaitu $PQ=22-8-4=10$. Sehingga keliling yang diarsir adalah:
$\begin{align} K &= AB+BQ+QP+PS+SR+RC+CD+DA \\ &= 26+8+10+10+10+4+26+22 \\ &= 34+30+52 \\ &= 116 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 116\ cm$

39. Soal TUK Masuk SMA Unggul DEL 2022 |*Soal Lengkap

Perhatikan gambar berikut:

Luas segitiga $ABC$ adalah $100\ \text{cm}^{2}$. Panjang $BD=\dfrac{1}{4} BC$, dan panjang $BD=\dfrac{2}{3} BC$. Luas segitiga $AED$ adalah...

$(A)\ 35\ \text{cm}^{2} $

$(B)\ 40\ \text{cm}^{2} $

$(C)\ 45\ \text{cm}^{2} $

$(D)\ 50\ \text{cm}^{2} $

Alternatif Pembahasan:

Dari informasi pada gambar di atas, dan bantuan perbandingan luas dua segitiga untuk tinggi segitiga sama dapat kita peroleh beberapa persamaan seperti berikut ini:

Perhatikan $\bigtriangleup ABD$ dan $\bigtriangleup ABC$ adalah segitiga dengan tinggi sama yaitu jarak $A$ ke $BC$, sehingga dapat kita peroleh:
$\begin{align} \dfrac{[ABD]}{[ABC]} & =\dfrac{1}{4} \\ \dfrac{[ABD]}{100} & =\dfrac{1}{4} \\ [ABD] & =\dfrac{1}{4}\ \times 100 \\ [ABD] & = 25 \end{align}$

Perhatikan $\bigtriangleup ADC$ dan $\bigtriangleup ADE$ adalah segitiga dengan tinggi sama tinggi sama yaitu jarak $D$ ke $AC$, sehingga dapat kita peroleh:
$\begin{align} \dfrac{[ADC]}{[ADE]} & =\dfrac{3}{2} \\ \dfrac{75}{[ADE]} & =\dfrac{3}{2} \\ [ADE] & =\dfrac{2}{3}\ \times 75 \\ [ADE] & = 50 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 50\ \text{cm}^{2}$

40. Soal Simulasi US Matematika SMP |*Soal Lengkap

Perhatikan gambar berikut

Jika panjang $AB=\left( 6x-31\right)\ \text{cm}$, $CD=\left( 3x- 1\right)\ \text{cm}$ dan $BC=\left( 2x+3 \right)\ \text{cm}$, maka panjang $AD= \cdots \text{cm}$

$(A)\ 29 $

$(B)\ 26 $

$(C)\ 23 $

$(D)\ 20 $

Alternatif Pembahasan:

Dari informasi pada soal dan gambar dapat kita peroleh:
$\begin{align}
AB &= CD \\ 6x-31 &= 3x- 1 \\ 6x-3x &= 31-1 \\ 3x &= 30 \\ x &= \dfrac{30}{3} = 10 \\ \hline AD &= BC \\ &= 2x+3 \\ &= 2(10)+3 \\ &= 23 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 23$

41. Soal Masuk SMA Unggulan - SMA Favorit |*Soal Lengkap

Luas persegi $ABCD$ yang memiliki koordinat $A \left(3,0 \right)$ dan $B \left( 2,2 \right)$ adalah...

$(A)\ 2\ \text{satuan luas} $

$(B)\ 3\ \text{satuan luas} $

$(C)\ 5\ \text{satuan luas} $

$(D)\ 6\ \text{satuan luas} $

Alternatif Pembahasan:

Sebuah persegi dengan titik sudutnya adalah koordinat $A \left(3,0 \right)$ dan $B \left( 2,2 \right)$, sehingga panjang rusuk kubus adalah jarak titik $A$ dan $B$ yaitu:
$\begin{align}
AB & = \sqrt{\left(x_{2}-x_{1} \right)^{2} + \left(y_{2}-y_{1} \right)^{2}} \\ AB & = \sqrt{\left(3-2 \right)^{2} + \left(0-2 \right)^{2}} \\ AB & = \sqrt{1 + 4} = \sqrt{5} \\ \hline \left[ABCD \right] & = AB \times AB \\ & = \sqrt{5} \times \sqrt{5} \\ & = 5 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 5\ \text{satuan luas}$

42. Model Soal US-UM Matematika SMP |*Soal Lengkap

Diketahui keliling pesegi panjang $36\ cm$ dengan panjang $(3x+2)$ cm dan lebar $(4x-5)$ cm, maka panjang dan lebar persegi panjang beruturut-turut adalah...

$(A)\ 22\ cm\ \text{dan}\ 7\ cm $

$(B)\ 19\ cm\ \text{dan}\ 11\ cm $

$(C)\ 11\ cm\ \text{dan}\ 7\ cm $

$(D)\ 10\ cm\ \text{dan}\ 4\ cm $

Alternatif Pembahasan:

Dari informasi pada soal dapat kita peroleh:
$\begin{align}
\text{Keliling} &= 36 \\
2p+2l &= 36 \\
2(3x+2)+2(4x-5) &= 36 \\
6x+4+8x-10 &= 36 \\
14x-6 &= 36 \\
14x &= 36+6 \\
14x &= 42 \\
x &= \dfrac{42}{14}\ \longrightarrow x=3 \end{align}$

Untuk $x = 3$ maka panjang $p=3x+2=11$ dan lebar $l=4x-5=7.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 11\ cm\ \text{dan}\ 7\ cm $

43. Model Soal US-UM Matematika SMP |*Soal Lengkap

Suatu taman berbentuk persegipanjang memiliki panjang diagonal $(4x+10)$ meter dan $(6x-2)$ meter. Panjang diagonal taman sebenarnya adalah...meter

$(A)\ 34\ m $

$(B)\ 24\ m $

$(C)\ 12\ m $

$(D)\ 6\ m $

Alternatif Pembahasan:

Panjang diagonal sebuah persegi panjang adalah sama, sehingga berlaku:
$\begin{align}
4x+10 &= 6x-2 \\
4x-6x &= -2-10 \\
-2x &= -12\ \longrightarrow x=6 \end{align}$
Panjang diagonal adalah $ 4x+10=4(6)+10=34$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 34\ m$

44. Model Soal US-UM Matematika SMP |*Soal Lengkap

Perhatikan sifat-sifat bangun datar berikut!

1. mempunyai dua pasang sisi yang sama panjang.
2. mempunyai diagonal yang saling tegak lurus.
3. mempunyai sudut siku-siku.
4. mempunyai $2$ pasang sisi sejajar.
5. mempunyai sepasang sudut sama besar.

Dari sifat-sifat di atas yang merupakan sifat laying-layang adalah...

$(A)\ 1, 2, 3$

$(B)\ 1, 3, 4$

$(C)\ 1, 3, 5$

$(D)\ 1, 2, 5$

Alternatif Pembahasan:

Dari informasi pada soal yang merupakan sifat layang-layang adalah sifat 1,2,5. Perhatikan gambar!

$\therefore$ Pilihan yang sesuai adalah $(D)\ 1, 2, 5$

45. Model Soal US-UM Matematika SMP |*Soal Lengkap

Suatu lapangan berbentuk persegi panjang dengan luas $120\ m^{2}$. Panjang lapangan tersebut adalag $12\ m$. Berapakah kelilingnya?

$(A)\ 22\ \text{m}$

$(B)\ 24\ \text{m}$

$(C)\ 42\ \text{m}$

$(D)\ 44\ \text{m}$

Alternatif Pembahasan:

Dari aturan menghitung luas persegi panjang $L=\text{p} \times \text{l}$, dapat kita peroleh:
$\begin{align}
L &= \text{p} \times \text{l} \\ 120 &= 12 \times \text{l} \\ \text{l} &= \dfrac{120}{12}=10 \\ \hline \text{keliling} &= 2 \left( \text{p}+\text{l} \right) \\ \text{keliling} &= 2 \left( 12+10 \right) \\ &= 2(22) =44 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 44\ \text{m}$

46. Contoh Soal PAS Genap Matematika SMP/MTs |*Soal Lengkap

Perhatikan gambar belahketupat $ABCD$ berikut. Jika $AD = (2x + 5)\ \text{cm}$, $BC = (x + 8)\ \text{cm}$, maka panjang $AD$ adalah...

$(A)\ 2\ \text{cm}$

$(B)\ 3\ \text{cm}$

$(C)\ 9\ \text{cm}$

$(D)\ 11\ \text{cm}$

Alternatif Pembahasan:

Dari salah satu ciri-ciri belahketupat, yaitu panjang keempat sisinya sama panjang, sehingga kita peroleh:
$\begin{align}
AD &= BC \\ 2x + 5 &= x + 8 \\ 2x-x &= 8-5 \\ x &= 3 \\ \hline AD &= 2x+5 \\ &= 2(3)+5 = 11 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 11\ \text{cm}$

47. Contoh Soal PAS Genap Matematika SMP/MTs |*Soal Lengkap

Suatu tanah lapang berbentuk persegipanjang memiliki luas $84\ \text{m}^{2}$ dengan panjang $12\ \text{m}$. Lebar tanah lapang tersebut adalah...

$(A)\ 0,7\ \text{cm}$

$(B)\ 7\ \text{cm}$

$(C)\ 70\ \text{cm}$

$(D)\ 700\ \text{cm}$

Alternatif Pembahasan:

Kita ketahui luas persegi panjang adalah panjang $\times$ lebar, sehingga kita peroleh:
$\begin{align}
L &= p \times l \\ 84\ \text{m}^{2} &= 12\ \text{m} \times l \\ l &= \dfrac{84}{12}\ \text{m} \\ l &= 7\ \text{m} = 700\ \text{cm} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 700\ \text{cm}$

48. Contoh Soal PAS Genap Matematika SMP/MTs |*Soal Lengkap

Pehatikan gambar persegi $ABCD$ dan persegi panjang $EFGH$ berikut. Jika luas daerah diarsir adalah $20\ \text{cm}^{2}$, maka luas daerah yang tidak diarsir adalah...

$(A)\ 104\ \text{cm}^{2}$

$(B)\ 94\ \text{cm}^{2}$

$(C)\ 84\ \text{cm}^{2}$

$(D)\ 74\ \text{cm}^{2}$

Alternatif Pembahasan:

Gambar di atas kita coba bagi menjadi tiga bagian yaitu, bagian $[x]$, $[y]$ dan $[20]$, seperti gambar berikut;

Kita ketahui persegi $ABCD$ luasnya adalah:
$\begin{align} \left[ ABCD \right] &= AB \times CD \\ \left[ ABCD \right] &= 8\ \text{cm} \times 8\ \text{cm}\\ \left[ x \right] + \left[ 20 \right] &= 64\ \text{cm}^{2}\\ x + &= 64\ \text{cm}^{2} -20\ \text{cm}^{2} =44\ \text{cm}^{2} \end{align}$

berikutnya persegi panjang $EFGH$ luasnya adalah:
$\begin{align} \left[ EFGH \right] &= EF \times FG \\ \left[ EFGH \right] &= 10\ \text{cm} \times 6\ \text{cm} \\ \left[ y \right] + \left[ 20 \right] &= 60\ \text{cm}^{2} \\ y &= 60 -20 =40\ \text{cm}^{2} \end{align}$

Luas keseluruhan yang tidak diarsir adalah $x+y=40+44=84\ \text{cm}^{2}$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 84\ \text{cm}^{2}$

49. Contoh Soal PAS Genap Matematika SMP/MTs |*Soal Lengkap

Perhatikan gambar jajargenjang $ABCD$ berikut. Luasnya adalah...

$(A)\ 120\ \text{cm}^{2}$

$(B)\ 96\ \text{cm}^{2}$

$(C)\ 80\ \text{cm}^{2}$

$(D)\ 70\ \text{cm}^{2}$

Alternatif Pembahasan:

Dari gambar jajargenjang di atas, tinggi jajar genjang yang diketahui $DE=7\ \text{cm}$ dan alasnya $BC=10\ \text{cm}$, sehingga luanya adalah:
$\begin{align} \left[ ABCD \right] &= \text{alas} \times \text{tinggi} \\ \left[ ABCD \right] &= 10\ \text{cm} \times 7\ \text{cm}\\ &= 70\ \text{cm}^{2} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 70\ \text{cm}^{2}$

50. Contoh Soal PAS Genap Matematika SMP/MTs |*Soal Lengkap

Perhatikan gambar trapesium berikut. Luasnya adalah...

$(A)\ 25\ \text{cm}^{2}$

$(B)\ 54\ \text{cm}^{2}$

$(C)\ 60\ \text{cm}^{2}$

$(D)\ 75\ \text{cm}^{2}$

Alternatif Pembahasan:

Untuk menghitung luas trapesium kita butuhkan jumlah garis sejajar dan tinggi. Dari gambar trapesium di atas belum diketaui tinggi trapesium. Dengan menggunakan teorema pythagoras dan unsur-unsur yang sudah diketahui dapat kita ketahui seperti berikut ini:

Dari gambar di atas dapat kita peroleh tinggi trapesium $t$ dengan menggunakan teorema pythagoras, yaitu:
$\begin{align} 5^{2} &= 3^{2} + t^{2} \\ 25 &= 9 + t^{2} \\ t^{2} &= 25-9 \\ t &= \sqrt{16}=4 \end{align}$

Untuk $t=4$, maka luas trapesium adalah:
$\begin{align} \left[ Trapesium \right] &= \dfrac{1}{2} \times \text{Jumlah Garis Sejajar} \times \text{t} \\ &= \dfrac{1}{2} \times (12+15) \times 4 \\ &= 54\ \text{cm}^{2} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 54\ \text{cm}^{2}$

51. Contoh Soal PAS Genap Matematika SMP/MTs |*Soal Lengkap

Belah ketupat $PQRS$ dengan panjang diagonal $8\ \text{cm}$ dan $6\ \text{cm}$. Keliling belah ketupat tersebut adalah...

$(A)\ 48\ \text{cm}$

$(B)\ 40\ \text{cm}$

$(C)\ 24\ \text{cm}$

$(D)\ 20\ \text{cm}$

Alternatif Pembahasan:

Dari informasi pada soal, belah ketupat dapat kita gambarkan menjadi seperti berikut ini:

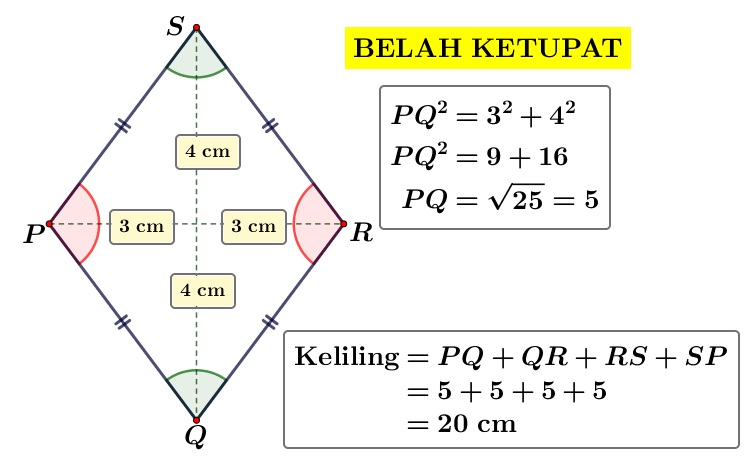
$\therefore$ Pilihan yang sesuai adalah $(D)\ 20\ \text{cm}$

52. Contoh Soal PAS Genap Matematika SMP/MTs |*Soal Lengkap

Perhatikan gambar $\bigtriangleup ABC$ berikut. Luasnya adalah ...

$(A)\ 30\ \text{cm}^{2}$

$(B)\ 60\ \text{cm}^{2}$

$(C)\ 90\ \text{cm}^{2}$

$(D)\ 120\ \text{cm}^{2}$

Alternatif Pembahasan:

Untuk menghitung luas $\bigtriangleup ABC$ kita perlukan alas dan tinggi segitiga dan pada gambar di atas belum diketahui tinggi segitiga.

Dari gambar di atas dapat kita peroleh luas $\bigtriangleup ABC$ adalah:
$\begin{align} \left[ ABC\right] &= \dfrac{1}{2} \times \text{alas} \times \text{t} \\ &= \dfrac{1}{2} \times 10 \times 12 \\ &= 60\ \text{cm}^{2} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 60\ \text{cm}^{2}$

53. Soal Seleksi Masuk YASOP - SMAN 2 Balige |*Soal Lengkap

Panjang sisi sejajar pada trapesium sama kaki $ABCD$ adalah $m$ dan $2m$. Jarak dua sisi tersebut adlaah $m-2$. Jika luas trapesium tersebut adalah $36\ cm^{2}$, maka keliling trapesium tersebut adalah...

$(A)\ 23\ \text{cm} $

$(B)\ 24\ \text{cm} $

$(C)\ 28\ \text{cm} $

$(D)\ 32\ \text{cm} $

Alternatif Pembahasan:

Dari informasi pada soal, jika kita gambarkan trapesium $ABCD$ adalah seperti berikut ini:

Dari gambar di atas kita peroleh:
$\begin{align} \left[ ABCD \right] &= \dfrac{1}{2} \times EC \left(AB+CD \right) \\ 36 &= \dfrac{1}{2} \times \left( m-2 \right) \left( m+2m \right) \\ 72 &= \left( m-2 \right) \left( 3m \right) \\ 72 &= 3m^{2}-6m \\ 24 &= m^{2}-2m \\ 0 &= m^{2}-2m-24 \\ 0 &= \left( m-6 \right)\left( m-4 \right) \\ 0 & m=6\ \text{atau}\ m=4 \end{align}$

Untuk $m=6$, dengan menggunakan teorema pythagoras kita peroleh panjang kaki trapesium adalah $5$, sehingga keliling trapesium adalah $K=6+5+12+5=28$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 28\ \text{cm} $

54. Soal Seleksi Masuk YASOP - SMAN 2 Balige |*Soal Lengkap

Selisih panjang sisi sejajar trapesium siku-siku adalah $4$. Jarak kedua sisi tersebut adalah dua kurangnya dari sisi sejajar terkecil. Jika luas trapesium adalah $36\ cm^{2}$, maka keliling trapesium tersebut adalah...

$(A)\ 18\ \text{cm} $

$(B)\ 22\ \text{cm} $

$(C)\ 25\ \text{cm} $

$(D)\ 27\ \text{cm} $

Alternatif Pembahasan:

Dari informasi pada soal, jika kita gambarkan trapesium $ABCD$ adalah seperti berikut ini:

Dari gambar di atas kita peroleh:
$\begin{align} \left[ ABCD \right] &= \dfrac{1}{2} \times EC \left(AB+CD \right) \\ 21 &= \dfrac{1}{2} \times \left( a-6 \right) \left( a+a-4 \right) \\ 42 &= \left( a-6 \right) \left( 2a-4 \right) \\ 42 &= 2a^{2}-4a-12a+24 \\ 0 &= 2a^{2}-16a-18 \\ 0 &= a^{2}-8a-9 \\ 0 &= \left( a-9 \right)\left( a+1 \right) \\ 0 & a=9\ \text{atau}\ a-1 \end{align}$

Untuk $a=9$, dengan menggunakan teorema pythagoras kita peroleh panjang kaki trapesium yang miring adalah $5$, sehingga keliling trapesium adalah $K=9+5+5+3=22$.

$\therefore$ Pilihan yang sesuai adalah $(B)\ 22\ \text{cm} $

55. Soal Masuk SMA Unggulan - SMA Favorit |*Soal Lengkap

Jika panjang sisi persegi pada gambar adalah $20\ \text{cm}$. Luas daerah yang diarsir adalah...

$(A)\ 70\ \text{cm}^{2} $

$(B)\ 80\ \text{cm}^{2} $

$(C)\ 90\ \text{cm}^{2} $

$(D)\ 100\ \text{cm}^{2} $

Alternatif Pembahasan:

Luas persegi adalah $20\ \text{cm} \times 20\ \text{cm} =400\ \text{cm}^{2}$. Jika kita perhatikan persegi dapat kita gambarkan seperti berikut ini:

Dari gambar di atas, dapat kita simpulkan bahwa luas persegi sama dengan $5$ kali luas persegi kecil (arsir), sehingga luas persegi kecil atau yang di arsir adalah $\dfrac{1}{5} \times 400\ \text{cm}^{2}=80\ \text{cm}^{2}$.

Alternatif lain dapat dengan menggunakan perbandingan sisi-sisi yang bersesuaian, lalau memanfaatkan luas segitiga dan persegi.

Luas segitiga besar adalah:
$\begin{align}
L_{{\color{blue}{\triangle}}} &= \dfrac{1}{2} \times 20\ \text{cm} \times 10\ \text{cm} \\
L_{{\color{blue}{\triangle}}} &= 100\ \text{cm}^{2} \end{align}$

Dari segitiga besar $ABC$ dapat kita peroleh:
$\begin{align}
AC^{2} &= AB^{2}+ BC^{2} \\
AC^{2} &= 20^{2}+ 10^{2} \\
AC^{2} &= 400+ 100 \\
AC &= \sqrt{500}=10\sqrt{5} \end{align}$

Segitiga besar $ABC$ dan segitiga kecil $ADE$ merupakan segitiga yang sebangun, sehingga kita peroleh:
$\begin{align} \dfrac{BC}{AC} &= \dfrac{DE}{AE} \\ \dfrac{10}{10\sqrt{5}} &= \dfrac{DE}{10} \\ \dfrac{10}{\sqrt{5}} &= DE \\ 2\sqrt{5} &= DE \\ \hline \\ \dfrac{AB}{AC} &= \dfrac{AD}{AE} \\ \dfrac{20}{10\sqrt{5}} &= \dfrac{AD}{10} \\ \dfrac{20}{\sqrt{5}} &= AD \\ 4\sqrt{5} &= AD \end{align}$

Untuk $DE=2\sqrt{5}$ dan $AD=4\sqrt{5}$ maka luas segitiga $ADE$ adalah:
$\begin{align} \left[ADE \right] &= \dfrac{1}{2} \times AD \times DE \\ \left[ADE \right] &= \dfrac{1}{2} \times 4\sqrt{5} \times 2\sqrt{5} \\ \left[ADE \right] &= 20 \end{align}$

segitiga besar terdiri dari dua segitiga kecil dan satu segi empat, sehingga dapat kita peroleh:
$\begin{align}
L_{{\color{blue}{\triangle}}} &= 2 \times \left[\text{segitiga kecil} \right] + \left[\text{segi empat} \right] \\
100\ \text{cm}^{2} &= 2 \times 20\ \text{cm}^{2} + \left[\text{segi empat} \right] \\
100\ \text{cm}^{2} &= 40\ \text{cm}^{2} + \left[\text{segi empat} \right] \\
60\ \text{cm}^{2} &= \left[\text{segi empat} \right] \\
\end{align}$

Persegi terdiri dari empat segi empat, empat segitiga kecil, dan daerah yang di arsir, sehingga dapat kita peroleh:
$\begin{align}
L_{\text{persegi}} &= 4 \times \left[\text{Luas segi empat} \right] + 4 \times \left[\text{Luas segitiga} \right] + \left[\text{Luas Arsir} \right] \\
400 &= 4 \times 60 + 4 \times 20 + \left[\text{Luas Arsir} \right] \\
400 &= 240 + 80 + \left[\text{Luas Arsir} \right] \\
400 &= 320 + \left[\text{Luas Arsir} \right] \\
80 &= \left[\text{Luas Arsir} \right] \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 80\ \text{cm}^{2}$

Catatan Soal dan Pembahasan Bangun Datar (Segitiga dan Segiempat) Matematika SMP di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.

JADIKAN HARI INI LUAR BIASA!
Ayo Share (Berbagi) Satu Hal Baik.

Jika ingin sukses harus pintar, Jika ingin pintar maka harus belajar, dan Jika ingin belajar harus rajin membaca.

Nie Ing Han