Calon guru belajar matematika dasar SMA lewat Soal dan Pembahasan Matematika Dasar SMA tentang Lingkaran. Materi lingkaran, mungkin salah satu materi paling umum kita dengar di matematika. Sejak duduk di Sekolah Dasar, lingkaran sudah diperkenalkan melalui ban sepeda yang sering kita mainkan lalu dihubungkan dengan jari-jari pada lingkar roda sepeda.
Penerapan lingkaran dalam kehidupan sehari-hari juga sangat banyak, yang paling sederhana seperti yang kita sebutkan di awal yaitu lingkar ban sepeda yang berbentuk lingkaran.
Mempelajari dan menggunakan aturan-aturan pada lingkaran tidaklah sulit, jika kita mengikuti step by step pembahasan yang kita diskusikan di bawah ini, maka kita akan dengan mudah memahami pembahasan soal lingkaran dan kita harapkan dapat meningkatkan daya nalar atau cara berpikir kita untuk menyelesaikan soal-masalah yang kita hadapi pada kehidupan sehari-hari.
Kesulitan menganalisa kalimat soal jadi salah satu masalah paling umum dalam diskusi menyelesaikan soal tentang lingkaran. Mudah-mudahan diksusi kita berikut ini menambah pemahaman kita tentang lingkaran.
Bahan latihan soal lingkaran yang kita pilih adalah soal dari soal UTBK SBMPTN (Seleksi Bersama Masuk Perguruan Tinggi Negeri), Soal Ujian Mandiri masuk PTN (SIMAK UI, UTUL UGM, UM UNDIP, dan sebagainya), Soal Ujian Masuk Sekolah Kedinasan atau Soal UN (Ujian Nasional) SMA.
Sebagai catatan, berikut kita tuliskan beberapa aturan dasar pada Lingkaran yang mungkin membantu dalam menyelesaikan masalah tentang lingkaran.
PERSAMAAN LINGKARAN
- Pusat $(0,0)$ dengan jari-jari $r$
$\Leftrightarrow $ Persamaan Lingkaran $x^{2}+y^{2}=r^{2}$ - Pusat $(a,b)$ dengan jari-jari $r$
$\Leftrightarrow $ Persamaan Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$ - Persamaan Umum Lingkaran $x^{2}+y^{2}+Ax+By+C=0$
$\Leftrightarrow $ Pusat $\left (-\frac{1}{2}A,-\frac{1}{2}B \right )$ dengan jari-jari $r=\sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C}$
Hubungan Titik $A(p,q)$ Pada lingkaran $L:x^{2}+y^{2}=r^{2}$
- Jika nilai $K=p^{2}+q^{2}$ dan $K \gt r^{2}$ maka titik $A$ di luar $L$;
- Jika nilai $K=p^{2}+q^{2}$ dan $K = r^{2}$ maka titik $A$ tepat pada $L$;
- Jika nilai $K=p^{2}+q^{2}$ dan $K \lt r^{2}$ maka titik $A$ di dalam $L$;
Hubungan Titik $A(p,q)$ Pada lingkaran $L:(x-a)^{2}+(y-b)^{2}=r^{2}$
- Jika nilai $K=(p-a)^{2}+(q-b)^{2}$ dan $K \gt r^{2}$ maka titik $A$ di luar $L$;
- Jika nilai $K=(p-a)^{2}+(q-b)^{2}$ dan $K = r^{2}$ maka titik $A$ tepat pada $L$;
- Jika nilai $K=(p-a)^{2}+(q-b)^{2}$ dan $K \lt r^{2}$ maka titik $A$ di dalam $L$;
Hubungan Titik $A(p,q)$ Pada lingkaran $L:x^{2}+y^{2}+Ax+By+C=0$
- Jika nilai $K=p^{2}+q^{2}+Ap+Bq+C$ dan $K \gt 0$ maka titik $A$ di luar $L$;
- Jika nilai $K=p^{2}+q^{2}+Ap+Bq+C$ dan $K = 0$ maka titik $A$ tepat pada $L$;
- Jika nilai $K=p^{2}+q^{2}+Ap+Bq+C$ dan $K \lt 0$ maka titik $A$ di dalam $L$;
Hubungan garis dengan lingkaran
Misal Jika diketahui persamaan garis $y=mx+n$ dan lingkaran $L:x^{2}+y^{2}+Ax+By+C=0$, maka dengan mensubstitusi $y=mx+n$ ke lingkaran $L$ akan diperoleh persamaan kuadrat. Dari persamaan kuadrat persekutuan tersebut kita bisa peroleh nilai $D=b^{2}-4ac$
- Jika nilai $D \gt 0$ maka garis memotong lingkaran;
- Jika nilai $D = 0$ maka garis menyinggung lingkaran;
- Jika nilai $D \lt 0$ maka garis tidak memotong dan tidak menyinggung lingkaran;
Hubungan terkahir yang perlu kita ketahui yaitu hubungan dua lingkaran. Untuk menentukan hubungan dua lingkaran atau kedudukan dua lingkaran dapat kita tentukan dengan melihat nilai diskriminan $\left( D=b^{2}-4ac \right)$ persamaan kuadrat persekutuan kedua lingkaran dan nilai jari-jari kedua lingkaran.
Persamaan Garis Singgung (PGS) Lingkaran
- Jika diketahui titik singgung $(x_{1},y_{1})$ pada lingkaran
- Persamaan Lingkaran $x^{2}+y^{2}=r^{2}$
$\Leftrightarrow $ PGS: $xx_{1} +yy_{1} =r^{2}$ - Persamaan Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$
$\Leftrightarrow $ PGS: $(x-a)(x_{1}-a)+(y-b)(y_{1}-b)=r^{2}$ - Persamaan Lingkaran $x^{2}+y^{2}+Ax+By+C=0$
$\Leftrightarrow $ PGS: $xx_{1} +yy_{1}+\frac{1}{2}A(x+x_{1})+\frac{1}{2}B(y+y_{1})+C=0$ - Jika diketahui gradien garis singgung lingkaran $(m)$
- Persamaan Lingkaran $x^{2}+y^{2}=r^{2}$
$\Leftrightarrow $ PGS: $y=mx\pm r\sqrt{m^{2}+1}$ - Persamaan Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$
$\Leftrightarrow $ PGS: $y-b=m(x-a)\pm r\sqrt{m^{2}+1}$
Jarak Titik ke Titik
Jarak titik $\left( x_{1},y_{1} \right)$ ke titik $\left( x_{2},y_{2} \right)$ adalah:
$d= \sqrt{ \left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2}} $
Jarak Titik ke Garis
Jarak titik $\left( x_{1},y_{1} \right)$ ke garis $ax+by+c=0$ adalah:
$d=\left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right|$
Rumus Alternatif Persamaan Garis Singgung (PGS) lingkaran
- Persamaan Garis Singgung lingkaran dengan pusat $\left( x_{1},y_{1} \right)$ dan jari-jari $r$ yang sejajar dengan garis $ax+by+c=0$, adalah:
$ax+by=ax_{1}+by_{1} \pm r \sqrt{a^{2}+b^{2}}$ - Persamaan Garis Singgung lingkaran dengan pusat $\left( x_{1},y_{1} \right)$ dan jari-jari $r$ yang tegak lurus dengan garis $ax+by+c=0$, adalah:
$bx-ay=bx_{1}-ay_{1} \pm r \sqrt{a^{2}+b^{2}}$
Soal dan Pembahasan Matematika Dasar SMA Lingkaran
Soal-soal latihan Matematika Dasar Lingkaran berikut ini silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan Periksa Jawaban dan jika hasilnya belum memuaskan, pilih ⟳ Ulangi Tes untuk tes ulang. Ayo Tunjukkan Kemampuan Terbaikmu!
| Nama Peserta : | |
| Tanggal Tes : | |
| Jumlah Soal : | 44 soal |
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.
1. Soal UMPTN 1994 🔗
Jari-jari dan titik pusat lingkaran $4x^{2}+4y^{2}+4x-12y+1=0$ adalah...
Alternatif Pembahasan:
$\begin{align}
4x^{2}+4y^{2}+4x-12y+1 &= 0 \\
x^{2}+ y^{2}+ x-3y+\dfrac{1}{4} &= 0 \\
\hline
A=1,\ B=-3,\ & C= \dfrac{1}{4}
\end{align}$
$\begin{align}
\text{Pusat}\ &= \left (-\dfrac{1}{2}A,-\dfrac{1}{2}B \right ) \\
&= \left (-\dfrac{1}{2}(1),-\dfrac{1}{2}(-3) \right ) \\
&= \left (-\dfrac{1}{2} , \dfrac{3}{2} \right ) \\
\hline
r &= \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
&=\sqrt{\dfrac{1}{4}(1)^{2}+\dfrac{1}{4}(-3)^{2}-\dfrac{1}{4}} \\
&= \sqrt{\dfrac{1}{4} + \dfrac{9}{4} -\dfrac{1}{4}} \\
&= \sqrt{\dfrac{9}{4}} = \dfrac{3}{2}
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(B)\ \frac{3}{2}\ \text{dan}\ \left( -\frac{1}{2}, \frac{3}{2} \right)$
2. Soal SPMB 2005 Kode 280 🔗
Jika $a \lt 0$ dan lingkaran $x^{2}+y^{2}-ax+2ay+1=0$ mempunyai jari-jari $2$ maka koordinat pusat lingkaran adalah...
Alternatif Pembahasan:
$\begin{align}
x^{2}+y^{2}-ax+2ay+1 &= 0 \\
A=-a,\ B=2a,\ & C= 1
\end{align}$
$\begin{align}
r &= \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
r^{2} &= \frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C \\
2^{2} &= \dfrac{1}{4}(-a)^{2}+\dfrac{1}{4}(2a)^{2}-1 \\
4 &= \dfrac{1}{4}a^{2} + a^{2} - 1 \\
4+1 &= \dfrac{5}{4}a^{2} \\
5 \cdot \dfrac{4}{5} &= a^{2} \\
4 &= a^{2} \rightarrow a=\pm 2
\end{align}$
Karena $a \lt 0$ maka nilai $a$ yang memenuhi adalah $a=-2$, sehingga berlaku:
$\begin{align}
x^{2}+y^{2}-ax+2ay+1 &= 0 \\
x^{2}+y^{2}+2x-4y+1 &= 0 \\
A=2,\ B=-4,\ & C= 1 \\
\end{align}$
$\begin{align}
\text{Pusat}\ & = \left (-\dfrac{1}{2}A,-\dfrac{1}{2}B \right ) \\
& = \left (-\dfrac{1}{2}(2),-\dfrac{1}{2}(-4) \right ) \\
& = \left (-1 , 2 \right ) \\
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ \left( -1, 2 \right) $
3. Soal UN Matematika IPA 2006 🔗
Persamaan lingkaran dengan pusat $P(3,1)$ dan menyinggung garis $3x+4y+7=0$ adalah...
Alternatif Pembahasan:
Untuk menggambar atau membentuk persamaan lingkaran ada dua hal dasar yang harus kita ketahui yaitu titik pusat lingkaran dan jari-jari lingkaran.
Pada soal sudah diberitahu bahwa pusat $P(3,1)$.
Lingkaran menyinggung garis $3x+4y+7=0$ sehingga jari-jari lingkaran adalah jarak titik $P(3,1)$ ke garis $3x+4y+7=0$.
$\begin{align}
r = d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\
&= \left| \dfrac{(3)(3)+(4)(1)+7}{\sqrt{3^{2}+4^{2}}} \right| \\
&= \left| \dfrac{20}{\sqrt{25}} \right| = 4
\end{align}$
Persamaan lingkaran dengan pusat $P(3,1)$ dan $r=4$
$\begin{align}
(x-a)^{2}+(y-b)^{2} &= r^{2} \\
(x-3)^{2}+(y-1)^{2} &= 4^{2} \\
x^{2}+y^{2}-6x-2y+9+1 &= 16 \\
x^{2}+y^{2}-6x-2y-6 &= 0
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ x^{2}+y^{2}-6x-2y-6=0$
4. Soal SPMB 2003 🔗
Diketahui lingkaran $2x^{2}+2y^{2}-4x+3py-30=0$ melalui titik $(-2,1)$. Persamaan lingkaran yang sepusat tetapi panjang jari-jarinya dua kali panjang jari-jari lingkaran tersebut adalah...
Alternatif Pembahasan:
Untuk menggambar atau membentuk persamaan lingkaran ada dua hal dasar yang harus kita ketahui yaitu titik pusat lingkaran dan jari-jari lingkaran.
Lingkaran $2x^{2}+2y^{2}-4x+3py-30=0$ melalui titik $(-2,1)$ sehingga berlaku:
$\begin{align}
2x^{2}+2y^{2}-4x+3py-30 &= 0 \\
2(-2)^{2}+2(1)^{2}-4(-2)+3(1)p-30 &= 0 \\
8+2+8+3p-30 &= 0 \\
3p &= 12 \\
p &= 4
\end{align}$
Untuk $p=4$, maka persamaan lingkaran menjadi
$\begin{align}
2x^{2}+2y^{2}-4x+3py-30 &= 0 \\
2x^{2}+2y^{2}-4x+12y-30 &= 0 \\
x^{2}+ y^{2}-2x+6y-15 &= 0
\end{align}$
$\begin{align}
\text{Pusat}\ &= \left (-\dfrac{1}{2}A,-\dfrac{1}{2}B \right ) \\
&= \left(-\dfrac{1}{2}(-2),-\dfrac{1}{2}(6) \right ) \\
&= \left( 1, -3 \right) \\
\hline
r &= \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
&=\sqrt{\dfrac{1}{4}(-2)^{2}+\dfrac{1}{4}(6)^{2}-(-15)} \\
&=\sqrt{1+9+15} = 5
\end{align}$
Persamaan lingkaran dengan $P\left( 1, -3 \right)$ dan $r=2(5)=10$ adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x-1 \right)^{2}+\left( y+3 \right)^{2} &= 10^{2} \\
x^{2}+y^{2}-2x+6y+1+9 &= 100 \\
x^{2}+y^{2}-2x+6y-90 &= 0 \\
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ x^{2}+y^{2}-2x+6y-90=0$
5. Soal UMPTN 1992 🔗
Jika titik $(-5,k)$ terletak pada lingkaran $x^{2}+y^{2}+2x-5y-21=0$, nilai $k$ adalah...
Alternatif Pembahasan:
Titik $(-5,k)$ terletak pada lingkaran $x^{2}+y^{2}+2x-5y-21=0$, sehingga berlaku:
$\begin{align}
x^{2}+y^{2}+2x-5y-21 &= 0 \\
(-5)^{2}+k^{2}+2(-5)-5(k)-21 &= 0 \\
25+k^{2}-10-5k-21 &= 0 \\
k^{2}-5k-6 &= 0 \\
(k-6)(k+1) &= 0 \\
k=6\ \text{atau}\ k=-1 &
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ -1\ \text{atau}\ 6$
6. Soal UMPTN 2005 Kode 780 🔗
Jika lingkaran $x^{2}+y^{2}+6x+6y+c=0$ menyinggung garis $x=2$, maka nilai $c$ adalah...
Alternatif Pembahasan:
Untuk menggambar atau membentuk persamaan lingkaran ada dua hal dasar yang harus kita ketahui yaitu titik pusat lingkaran dan jari-jari lingkaran.
Pada lingkaran $x^{2}+y^{2}+6x+6y+c=0$ titik pusatnya adalah:
$\begin{align}
\text{Pusat}\ &= \left (-\dfrac{1}{2}A,-\dfrac{1}{2}B \right ) \\
&= \left(-\dfrac{1}{2}(6),-\dfrac{1}{2}(6) \right ) \\
&= \left( -3, -3 \right)
\end{align}$
Lingkaran $x^{2}+y^{2}+6x+6y+c=0$ menyinggung garis $x=2$ sehingga jari-jari lingkaran adalah jarak titik $P(-3,-3)$ ke garis $x=2$ yaitu $5$.
Jika belum bisa mendapatkan $r=5$ dengan membayangkan posisi lingkaran dengan garis dapat menghitung jarak $P(-3,-3)$ ke garis $x-2=0$ yaitu:
$\begin{align}
r = d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\
&= \left| \dfrac{(1)(-3)+(0)(-3)-2}{\sqrt{(1)^{2}+(0)^{2}}} \right| \\
&= \left| \dfrac{-5}{\sqrt{1}} \right| = 5
\end{align}$
Persamaan lingkaran dengan pusat $P(-3,-3)$ dan $r=5$
$\begin{align}
(x-a)^{2}+(y-b)^{2} &= r^{2} \\
(x+3)^{2}+(y+3)^{2} &= 5^{2} \\
x^{2}+y^{2}+6x+6y+9+9 &= 25 \\
x^{2}+y^{2}+6x+6y-7 &= 0
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ -7$
7. Soal SPMB 2006 Kode 420 🔗
Jika lingkaran $x^{2}+y^{2}+ax+by+c=0$ yang berpusat di $(1,-1)$ dan menyinggung garis $y=x$, maka nilai $a+b+c$ adalah...
Alternatif Pembahasan:
Untuk menggambar atau membentuk persamaan lingkaran ada dua hal dasar yang harus kita ketahui yaitu titik pusat lingkaran dan jari-jari lingkaran.
Pada lingkaran $x^{2}+y^{2}+ax+by+c=0$ titik pusatnya $(1,-1)$, sehingga berlaku:
$\begin{align}
\text{Pusat}\ &= \left (-\dfrac{1}{2}A,-\dfrac{1}{2}B \right ) \\
\left(1,-1 \right ) &= \left(-\dfrac{1}{2}(a),-\dfrac{1}{2}(b) \right ) \\
a &= -2 \\
b &= 2
\end{align}$
Untuk $a=-2$ dan $b=2$ maka persamaan lingkaran $x^{2}+y^{2}-2x+2y+c=0$.
Lingkaran $x^{2}+y^{2}-2x+2y+c=0$ menyinggung garis $y=x$ sehingga jari-jari lingkaran adalah jarak titik $P(1,-1)$ ke garis $x-y=0$, yaitu:
$\begin{align}
r = d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\
&= \left| \dfrac{(1)(1)+(-1)(-1)+0}{\sqrt{(1)^{2}+(-1)^{2}}} \right| \\
&= \left| \dfrac{2}{\sqrt{2}} \right| = \sqrt{2}
\end{align}$
Persamaan lingkaran dengan pusat $P(1,-1)$ dan $r=\sqrt{2}$
$\begin{align}
(x-a)^{2}+(y-b)^{2} &= r^{2} \\
(x-1)^{2}+(y+1)^{2} &= \left( \sqrt{2} \right)^{2} \\
x^{2}+y^{2}-2x+2y+1+1 &= 2 \\
x^{2}+y^{2}-2x+2y &= 0
\end{align}$
Dari persamaan di atas kita peroleh nilai $c=0$, sehingga $a+b+c=-2+2+0=0$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ 0$
8. Soal UMPTN 1994 🔗
Lingkaran yang melalui titik-titik $(4,2),\ (1,3)$ dan $(-3,-5)$ berjari-jari...
Alternatif Pembahasan:
Untuk membentuk persamaan lingkaran dari tiga titik yang dilalui lingkaran adalah dengan mensubstitusi nilai $(x,y)$ ke persamaan umum lingkaran $x^{2}+y^{2}+Ax+By+C= 0$. Setelah dapat tiga persamaan dengan dua variabel, lalu dilakukan substitusi atau eliminasi.
$\begin{align}
(4,2)\ & \rightarrow (4)^{2}+(2)^{2}+A(4)+B(2)+C= 0 \\
& \rightarrow 4A +2B +C= -20\ \cdots (pers.1) \\
(1,3)\ & \rightarrow (1)^{2}+(3)^{2}+A(1)+B(3)+C= 0 \\
& \rightarrow A +3B +C= -10\ \cdots\ (pers.2) \\
(-3,-5)\ & \rightarrow (-3)^{2}+(-5)^{2}+A(-3)+B(-5)+C= 0 \\
& \rightarrow -3A -5B +C= -34\ \cdots\ (pers.3)
\end{align}$
Pertama, kita pilih mengeliminasi $C$ dari $(pers.1)$ dan $(pers.2)$
$\begin{array}{c|c|cc}
4A +2B +C= -20 & \\
A +3B +C= -10 & (-) \\
\hline
3A-B = -10\ \cdots\ (pers.4) &
\end{array} $
Kedua, kita mengeliminasi $C$ dari $(pers.2)$ dan $(pers.3)$
$\begin{array}{c|c|cc}
A +3B +C= -10 & \\
-3A -5B +C= -34 & (-) \\
\hline
4A+8B = 24\ & \\
A+2B = 6\ \cdots\ (pers.5) &
\end{array} $
Ketiga, kita mengeliminasi $A$ atau $B$ dari $(pers.4)$ dan $(pers.5)$
$\begin{array}{c|c|cc}
3A-B = -10 & (\times 2) \\
A+2B = 6 & (\times 1) \\
\hline
6A-2B = -20 & \\
A+2B = 6 & (+) \\
\hline
7A = -14 &
A = -2 &
\end{array} $
Keempat, kita substitusi $A=-2$ ke $(pers.4)$ atau $(pers.5)$
$\begin{align}
A+2B = 6\ & \rightarrow -2+2B = 6 \\
& \rightarrow 2B = 8 \\
& \rightarrow B = 4
\end{align}$
Kelima, kita substitusi $A=-2$ dan $B=4$ ke $(pers.1)$, $(pers.2)$ atau $(pers.3)$
$\begin{align}
4A +2B +C= -20\ & \rightarrow 4(-2) +2(4) +C= -20 \\
& \rightarrow -8 + 8 +C= -20 \\
& \rightarrow C = -20
\end{align}$
Untuk $A=-2$, $B=4$ dan $C=-20$, kita sudah dapat menentukan persamaan lingkran atau jari-jari lingkaran.
$\begin{align}
r &= \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
&=\sqrt{\frac{1}{4}(-2)^{2}+\frac{1}{4}(4)^{2}-(-20)} \\
&=\sqrt{1+4+20}=5
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 5$
9. Soal UMPTN 2001 Rayon C 🔗]
Jika garis $x=2y+5$ memotong lingkaran $x^{2}+y^{2}-4x+8y+10=0$ di titik $A$ dan $B$, maka panjang ruas garis $AB$ adalah...
Alternatif Pembahasan:
Titik potong lingkaran dan garis dapat kita ketahui dengan mensubsitusi $x=2y+5$ ke persamaan $x^{2}+y^{2}-4x+8y+10=0$.
$\begin{align}
x^{2}+y^{2}-4x+8y+10 & = 0 \\
(2y+5)^{2}+y^{2}-4(2y+5)+8y+10 & = 0 \\
4y^{2}+20y+25+y^{2}-8y-20+8y+10 & = 0 \\
5y^{2}+20y+15 & = 0 \\
y^{2}+4y+3 & = 0 \\
(y+3)(y+1) & = 0
\end{align}$
$y=-1\ \text{maka}\ x= 2(-1)+5=3$
$y=-3\ \text{maka}\ x= 2(-3)+5=-1$
Kita peroleh titik potong garis dan lingkaran adalah di $A(3,-1)$ dan $B(-1,-3)$, panjang ruas garis $AB$ adalah
$\begin{align}
d & = \sqrt{(-3+1)^{2}+(-1-3)^{2}} \\
& = \sqrt{4+16} \\
& = 2\sqrt{5}
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 2\sqrt{5}$
10. Soal UMPTN 1999 Rayon C 🔗
Jika garis $g:x-2y=5$ memotong lingkaran $x^{2}+y^{2}-4x+8y+10=0$ di titik $A$ dan $B$, maka luas segitiga yang dibentuk oleh $A$, $B$ dan pusat lingkaran adalah...
Alternatif Pembahasan:
kita ketahui bahwa jika garis $y=mx+n$ dan lingkaran $L:x^{2}+y^{2}+Ax+By+C=0$ berpotongan maka titik potong dapat diperoleh dari akar persamaan kuadrat persekutuan antara garis dan lingkaran.
Pertama, kita substitusi $x-2y=5$ ke $x^{2}+y^{2}-4x+8y+10=0$
$\begin{align}
x^{2}+y^{2}-4x+8y+10 &= 0 \\
(5+2y)^{2}+y^{2}-4(5+2y)+8y+10 &= 0 \\
4y^{2}+20y+25+y^{2}-20-8y+8y+10 &= 0 \\
5y^{2}+20y+15 &= 0 \\
y^{2}+4y+3 &= 0 \\
(y+1)(y+3) &= 0 \\
y=-1\ \text{atau}\ y=-3 &
\end{align}$
Untuk $y=-1$ kita peroleh $x=5+2y=5+2(-1)=3$, titik potong $(3,-1)$
Untuk $y=-3$ kita peroleh $x=5+2y=5+2(-3)=-1$, titik potong $(-1,-3)$
Jika kita gambarkan, titik potong garis dengan lingkaran dan segitiga yang disebutkan oleh soal, seperti berikut ini:

Dari gambar di atas dapat kita hitung luas segitiga adalah luas setengah persegi dimana panjang sisi persegi adalah:
$\begin{align}
d &= \sqrt{ \left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2}} \\
&= \sqrt{ \left(3-0 \right)^{2}+\left(-1-0 \right)^{2}} \\
&= \sqrt{ 9+1} = \sqrt{10}
\end{align}$
Luas segitiga adalah $\dfrac{1}{2} \cdot \sqrt{10} \cdot \sqrt{10} = 5$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 5$
11. Soal SPMB 2005 Kode 580 🔗
Lingkaran $L$ menyinggung sumbu-$x$, menyinggung lingkaran $x^{2}+y^{2}=4$ dan melalui titik $(4,6)$. Persamaan lingkaran $L$ adalah...
Alternatif Pembahasan:
Jika kita gambarkan, ilustrasi apa yang disampaikan pada soal kurang lebih seperti berikut ini:

- Lingkaran yang akan kita kita tentukan misalkan lingkaran dengan pusat $(a,b)$ dan jari-jari $r$ yaitu $(x-a)^{2}+(y-b)^{2}=r^{2}$.
- Lingkaran menyinggung sumbu-$x$ sehingga dengan pusat $(a,b)$, dapat kita tentukan bahwa $r=b$.
- Pada segitiga $PQR$ dapat kita terapkan teorema pythagoras,
$ \begin{align}
OP^{2} & = OQ^{2}+PQ^{2} \\ (r+2)^{2} & = a^{2}+r^{2} \\ r^{2}+4r+4 & = a^{2}+r^{2} \\ 4r+4 & = a^{2}
\end{align} $ - Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$ melalui titik $(4,6)$ sehingga berlaku:
$ \begin{align}
(x-a)^{2}+(y-b)^{2} &= r^{2} \\ (4-a)^{2}+(6-b)^{2} &= r^{2} \\ a^{2}-8a+16+b^{2}-12b+36 &= r^{2} \\ \hline
4r+4 = a^{2}\ \text{dan}\ b=r \\
\hline
4r+4-8a+16+r^{2}-12r+36 &= r^{2} \\ -8a+56 &= 8r \\ -a+7 &= r
\end{align} $
Untuk $r=-a+7$ dan $4r+4 = a^{2}$ kita peroleh:
$\begin{align}
4r+4 &= a^{2} \\
4(-a+7)+4 &= a^{2} \\
-4a+28+4 &= a^{2} \\
a^{2}+4a-32 &= 0 \\
(a+8)(a-4) &= 0 \\
a=-8\ \text{atau}\ a=4 &
\end{align}$
Dengan $a=4$, maka $b=r=-a+7=3$, sehingga persamaan lingkaran adalah:
$ \begin{align}
(x-a)^{2}+(y-b)^{2} &= r^{2} \\
(x-4)^{2}+(y-3)^{2} &= 3^{2} \\
x^{2}+y^{2}-8x-6y+16+9 &= 9 \\
x^{2}+y^{2}-8x-6y+16 &= 0
\end{align} $
$ \therefore $ Pilihan yang sesuai adalah $(C)\ x^{2}+y^{2}-8x-6y+16=0 $
12. Soal UM-UGM 2004 Kode 111 🔗
Diketahui sebuah lingkaran $L:x^{2}+y^{2}+2y-24=0$. Jika melalui titik $P(1,6)$ dibuat garis singgung pada $L$ maka jarak dari $P$ ke titik singgung tadi adalah...
Alternatif Pembahasan:
$\begin{align}
x^{2}+y^{2}+2y-24=0 &= 0 \\
A=0,\ B=2,\ C= -24 &
\end{align}$
$\begin{align} r &= \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\ r^{2} &= \frac{1}{4}(0)^{2}+\frac{1}{4}(2)^{2}-(-24) \\ r^{2} &= 1+24 \\ r &= \sqrt{25}=5 \end{align}$
$\begin{align} \text{Pusat}\ & = \left (-\dfrac{1}{2}A,-\dfrac{1}{2}B \right ) \\ & = \left (-\dfrac{1}{2}(0),-\dfrac{1}{2}(2) \right ) \\ & = \left (0 , -1 \right ) \\ \end{align}$
Jarak titik pusat $O \left (0 , -1 \right )$ ke $P\left (1 , 6 \right )$ adalah:
$\begin{align}
OP & = \sqrt{\left (0-1 \right )^{2}+\left (-1-6 \right )^{2}} \\
& = \sqrt{1+49} \\
& = \sqrt{50} \\
\end{align}$
Karena garis singgung tegak lurus dengan jari-jari, sehingga berlaku teorema pythagoras antara titik pusat, titik singgung dan titik $P$. Jarak titik singgung ke titik $P\left (1 , 6 \right )$ adalah:
$\begin{align}
d & = \sqrt{OP^{2}-r^{2}} \\
& = \sqrt{50-5^{2}} \\
& = \sqrt{25}=5
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(E)\ 5$
13. Soal SPMB 2006 Kode 621 🔗
Lingkaran dengan persamaan $x^{2}+y^{2}-2px+q=0$, $p \gt 0$ dan yang berjari-jari $2$ akan menyinggung garis $x-y=0$ bila $p$ sama dengan...
Alternatif Pembahasan:
Jari-jari lingkaran $x^{2}+y^{2}-2px+q=0$ adalah $2$, sehingga berlaku:
$\begin{align}
r &= \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
2 &=\sqrt{\frac{1}{4}(-2p)^{2}+\frac{1}{4}(0)^{2}-(q)} \\
2 &=\sqrt{p^{2}-q} \\
4 &= p^{2}-q
\end{align}$
Lingkaran $x^{2}+y^{2}-2px+q=0$ menyinggung garis $y=x$ sehingga diskriminan persamaan kuadrat persekutuan adalah nol;
$\begin{align}
x^{2}+(x)^{2}-2px+q &= 0 \\
2x^{2}-2px+q &= 0 \\
\hline
D=b^{2}-4ac &= 0 \\
(-2p)^{2}-4(2)(q) &= 0 \\
4p^{2}-8q &= 0 \\
p^{2}-2q &= 0 \\
p^{2}-q-q &= 0 \\
4-q &= 0 \\
q &=4
\end{align}$
Untuk $q=4$ maka kita peroleh nilai $p$
$\begin{align}
4 &= p^{2}-q \\
4 &= p^{2}-4 \\
8 &= p^{2} \\
2\sqrt{2} &= p
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(B)\ 2\sqrt{2}$
14. Soal SPMB 2005 Kode 480 🔗
Jika garis $y=\dfrac{1}{\sqrt{5}}\left( 2x+5 \right)$ menyinggung lingkaran $x^{2}+y^{2}-4x-k=0$, maka $k=\cdots$
Alternatif Pembahasan:
Lingkaran $x^{2}+y^{2}-4x-k=0$ menyinggung garis $y=\dfrac{1}{\sqrt{5}}\left( 2x+5 \right)$ sehingga diskriminan persamaan kuadrat persekutuan adalah nol;
$\begin{align}
x^{2}+y^{2}-4x-k &= 0 \\
x^{2}+\left( \dfrac{1}{\sqrt{5}}\left( 2x+5 \right) \right)^{2}-4x-k &= 0 \\
x^{2}+\dfrac{1}{5} \left( 2x+5 \right)^{2}-4x-k &= 0 \\
5x^{2}+ \left( 4x^{2}+20x+25 \right) -20x-5k &= 0 \\
9x^{2}+25-5k &= 0 \\
\hline
D=b^{2}-4ac &= 0 \\
(0)^{2}-4(9)(25-5k) &= 0 \\
0-900+180k &= 0 \\
180k &= 900 \\
k &= \dfrac{900}{180}=5
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(E)\ 5$
15. Soal SPMB 2006 Kode 320 🔗
Diketahui lingkaran berjari-jari $3$ dan berpusat di $(a,7)$ dengan $a$ bilangan bulat positif. Jika lingkaran tersebut menyinggung parabola $y=(a+2)+bx-x^{2}$ di titik puncak, maka $b=\cdots$
Alternatif Pembahasan:
Soal di atas adalah penggabungan materi lingkaran dan fungsi kuadrat, sehingga sedikit catatan tentang fungsi kuadrat mungkin perlu kita tampilkan yaitu:
Titik puncak parabola $y=ax^{2}+bx+c$ adalah $\left( -\dfrac{b}{2a}, -\dfrac{b^{2}-4ac}{4a} \right)$
Lingkaran berjari-jari $3$ dan berpusat di $(a,7)$ menyinggung puncak parabola $y=(a+2)+bx-x^{2}$, kemungkinannya hanya berada pada satu posisi, ilustrasinya seperti berikut ini:

Dari pusat lingkaran $(a,7)$ dan titik puncak parabola $\left( x_{p},y_{p} \right)$ dapat kita simpulan bahwa $x_{p}=a$ dan $y_{p}+3=7\ \rightarrow y_{p}=4$
$\begin{align}
x_{p} &= -\dfrac{b}{2a} \\
a &= -\dfrac{b}{2(-1)} \\
2a &= b \\
\hline
y_{p} &= -\dfrac{b^{2}-4ac}{4a} \\
4 &= -\dfrac{b^{2}-4(-1)(a+2)}{4(-1)} \\
16 &= b^{2}+4a+8 \\
0 &= b^{2}+4a-8 \\
0 &= b^{2}+2(b)-8 \\
0 &= (b+4)(b-2) \\
& b=-4\ \text{atau}\ b=2
\end{align}$
Karena $a$ bilangan bulat positif sehingga nilai $b$ yang memenuhi adalah $b=2$.
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 2$
16. Soal SBMPTN 2016 Kode 322 🔗
Diketahui dua buah lingkaran dengan titik pusat yang sama, berturut-turut berjari-jari $R_{1}$ dan $R_{2}$ dengan $R_{1} \gt R_{2}$. Jika panjang tali busur $AB=10$, maka selisih luas lingkaran tersebut adalah...
Alternatif Pembahasan:
Untuk menghitung Selisih luas lingkaran maka perhitungannya adalah;
$\pi R_{1}^{2}-\pi R_{2}^{2} $
$=\pi \left (R_{1}^{2}-R_{2}^{2} \right )$
Sampai pada perhitungan ini kita membutuhkan kuadrat selisih dari jari-jari lingkaran.

Dengan memperhatikan gambar diatas, $\bigtriangleup OAB$ adalah segitiga sama kaki. sehingga jika $OC$ merupakan garis tinggi, maka berlaku;
$\begin{align}
OA^{2} & = AC^{2}+OC^{2} \\
R_{1}^{2} & = 5^{2}+R_{2}^{2} \\
R_{1}^{2}-R_{2}^{2} & = 5^{2} \\
R_{1}^{2}-R_{2}^{2} & = 25
\end{align}$
Selisih luas kedua lingkaran adalah $ \pi \left(R_{1}^{2} - R_{2}^{2}\right) = \pi (25)= 25 \pi $
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 25 \pi$
17. Soal SBMPTN 2016 Kode 234 🔗
Titik $(0,b)$ adalah titik potong garis singgung persekutuan luar lingkaran luar $x^{2}+y^{2}=16$ dan $(x-8)^{2}+(y-8)^{2}=16$ dengan sumbu $y$. Nilai $b=\cdots$
Alternatif Pembahasan:
Apa yang disampaikan pada soal jika kita gambar, kurang lebih seperti tampak pada gambar berikut ini;

$g_{1}$ dan $g_{3}$ adalah garis singgung persekutuan luar lingkaran, sehingga garis singgung persekutuan luar lingkaran memotong sumbu $y$ di dua titik kemungkinan.
Untuk mengetahui koordinat titik $(0,b)$ kita cari tahu persamaan $g_{1}$ atau $g_{3}$, dapat kita ketahui dengan menggunakan persamaan garis singgung lingkaran dengan pusat $(0,0)$, $r=4$ dan gradien $m$
$y=mx\pm r\sqrt{1+m^{2}}$
$y=mx\pm 4\sqrt{1+m^{2}}$
Untuk mengetahui gradien $g_{1}$ kita hitung dari gradien $g_{2}$ karena $g_{1}$ sejajar dengan $g_{2}$ sehingga gradiennya sama.
Gradien $g_{2}$
$\begin{align}
m_{2} & = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\
m_{2} & = \frac{8-0}{8-2} \\
m_{2} & = 1 \\
m_{1} & = 1 \\
\end{align}$
Persamaan $g_{1}$ adalah
$y=mx\pm 4\sqrt{1+m^{2}}$
$y=x\pm 4\sqrt{1+1}$
$y=x\pm 4\sqrt{2}$
Saat garis $g_{1}$ memotong sumbu $y$ sehingga $x=0$ maka $y= 4\sqrt{2}$ atau $y= -4\sqrt{2}$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ 4\sqrt{2}$
18. Soal SBMPTN 2015 Kode 508 🔗
Misalkan titik $A$ dan $B$ pada lingkaran $x^{2}+y^{2}-6x-2y+k=0$ sehingga garis singgung lingkaran di titik $A$ dan $B$ berpotongan di $C(8,1)$. Jika luas segiempat yang melalui $A,B,C,$ dan pusat lingkaran adalah $12$, maka $k=\cdots$
Alternatif Pembahasan:
Apa yang disampaikan pada soal jika kita coba gambar, kurang lebih seperti tampak pada gambar berikut ini;

Luas $PABC$ adalah $\left [ PACB \right ]=OA\cdot AC$
$OA \cdot AC=12$
Dari persamaan lingkaran $x^{2}+y^{2}-6x-2y+k=0$ kita dapat nilai $r=OA$,
$\begin{align}
r & = \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
& = \sqrt{\frac{1}{4}(-6)^{2}+\frac{1}{4}(-2)^{2}-k} \\
& = \sqrt{10-k}
\end{align}$
Begitu juga dari $\bigtriangleup OAC$ kita dapat nilai $AC$.
$\begin{align}
OA^{2}+AC^{2} & = OC^{2} \\
r^{2}+AC^{2} & = 5^{2} \\
AC^{2} & = 5^{2}-r^{2} \\
& = 25-\left (10-k \right ) \\
& = 15+k \\
AC & = \sqrt{15+k}
\end{align}$
$\begin{align}
OA\ \cdot AC & = 12 \\
\sqrt{10-k} \cdot \sqrt{15+k} & = 12 \\
(10-k) \cdot (15+k) & = 144 \\
150-5k-k^{2} & = 144 \\
k^{2}+5k-6 & = 144 \\
(k+6)(k-1) & = 0
\end{align}$
Nilai $k$ yang memenuhi adalah $k=-6$ atau $k=1$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ 1$
19. Soal SBMPTN 2014 Kode 572/523 🔗
Persamaan garis lurus yang melalui titik potong lingkaran-lingkaran yang melalui titik $(-2,-1)$ dan menyinggung sumbu $x$ dan sumbu $y$ adalah...
Alternatif Pembahasan:
Dua lingkaran yang menyinggung sumbu $x$ dan sumbu $y$ jika kita gambarkan kurang lebih seperti gambar berikut:

Untuk lingkaran yang menyinggung sumbu $x$ dan sumbu $y$ mempunyai ciri-ciri khusus yaitu jika jari-jari $r=a$ maka titik pusat hanya ada 4 kemungkinan yaitu $(a,a)$ , $(-a,a)$, $(a,-a)$, dan $(-a,-a)$.
Pada soal dikatakan lingkaran melalui titik $(-2,-1)$ maka lingkaran yang dimaksud berada pada kwadran III sehingga titik pusat adalah $(-a,-a)$ dan persamaan lingkarannya adalah $\left (x+a \right )^{2}+\left (y+a \right )^{2}=a^{2}$.
Karena lingkaran melaui titik $(-2,-1)$ sehingga berlaku:
$\begin{align}
\left (-2+a \right )^{2}+\left (-1+a \right )^{2} & = a^{2} \\
4-4a+a^{2}+1-2a+a^{2} & = a^{2} \\
a^{2}-6a+5 & = 0 \\
(a-5)(a-1) & = 0 \\
a= 5\ \text{atau}\ a = 1 &
\end{align}$
Untuk $a=5$, persamaan lingkaran adalah
$\begin{align}
\left (x+a \right )^{2}+\left (y+a \right )^{2} &=a^{2} \\
\left (x+5 \right )^{2}+\left (y+5 \right )^{2} &=5^{2} \\
x^{2}+y^{2}+10x+10y+25 &=0
\end{align}$
Untuk $a=1$, persamaan lingkaran adalah
$\begin{align}
\left (x+a \right )^{2}+\left (y+a \right )^{2} &=a^{2} \\
\left (x+1 \right )^{2}+\left (y+1 \right )^{2} &=1^{2} \\
x^{2}+y^{2}+2x+2y+1 &=0
\end{align}$
Untuk mendapatkan persamaan garis yang melalui titik potong dua lingkaran, bisa dengan mengeliminasi kedua persamaan lingkaran.
$\begin{array}{c|c|cc}
x^{2}+y^{2}+10x+10y+25=0 & \\
x^{2}+y^{2}+2x+2y+1=0 & (-) \\
\hline
8x+8y+24=0 & \\
x+ y+3=0
\end{array} $
$ \therefore $ Pilihan yang sesuai adalah $(C)\ x+y+3=0$
20. Soal SBMPTN 2014 Kode 532 🔗
Persamaan garis lurus yang melalui titik potong lingkaran-lingkaran yang melalui titik $(2,-1)$ dan menyinggung sumbu $x$ dan sumbu $y$ adalah...
Alternatif Pembahasan:
Dua lingkaran yang menyinggung sumbu $x$ dan sumbu $y$ jika kita gambarkan kurang lebih seperti gambar berikut:

Untuk lingkaran yang menyinggung sumbu $x$ dan sumbu $y$ mempunyai ciri-ciri khusus yaitu jika jari-jari $r=a$ maka titik pusat hanya ada 4 kemungkinan yaitu $(a,a)$ , $(-a,a)$, $(a,-a)$, dan $(-a,-a)$.
Pada soal dikatakan lingkaran melalui titik $(2,-1)$ maka lingkaran yang dimaksud berada pada kwadran IV sehingga titik pusat adalah $(a,-a)$ dan persamaan lingkarannya adalah $\left (x-a \right )^{2}+\left (y+a \right )^{2}=a^{2}$.
karena lingkaran melaui titik $(2,-1)$ sehingga berlaku:
$\begin{align}
\left (2-a \right )^{2}+\left (-1+a \right )^{2} & = a^{2} \\
4-4a+a^{2}+1-2a+a^{2} & = a^{2} \\
a^{2}-6a+5 & = 0 \\
(a-5)(a-1) & = 0 \\
a= 5\ \text{atau}\ a = 1 &
\end{align}$
Untuk $a=5$, persamaan lingkaran adalah
$\begin{align}
\left (x-a \right )^{2}+\left (y+a \right )^{2} &=a^{2} \\
\left (x-5 \right )^{2}+\left (y+5 \right )^{2} &=5^{2} \\
x^{2}+y^{2}-10x+10y+25 &=0
\end{align}$
Untuk $a=1$, persamaan lingkaran adalah
$\begin{align}
\left (x-a \right )^{2}+\left (y+a \right )^{2} &=a^{2} \\
\left (x-1 \right )^{2}+\left (y+1 \right )^{2} &=1^{2} \\
x^{2}+y^{2}-2x+2y+1 &=0
\end{align}$
Untuk mendapatkan persamaan garis yang melalui titik potong dua lingkaran, bisa dengan mengeliminasi kedua persamaan lingkaran.
$\begin{array}{c|c|cc}
x^{2}+y^{2}-10x+10y+25=0 & \\
x^{2}+y^{2}-2x+2y+1=0 & (-) \\
\hline
-8x+8y+24=0 & \\
-x+ y+3=0 & \\
x- y-3=0
\end{array} $
$ \therefore $ Pilihan yang sesuai adalah $(C)\ x-y-3=0$
21. Soal SBMPTN 2014 Kode 512/514 🔗
Jika lingkaran $x^{2}+y^{2}-2ax+b=0$ mempunyai jari-jari $2$ dan menyinggung $x-y=0$, maka nilai $a^{2}+b$ adalah...
Alternatif Pembahasan:
Lingkaran $x^{2}+y^{2}-2ax+b=0$ mempunyai jari-jari $r=2$
$\begin{align}
r & = \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
2 & = \sqrt{\frac{1}{4}(-2a)^{2}-b} \\
4 & = a^{2}-b\ \cdots\ (1)
\end{align}$
Lingkaran $x^{2}+y^{2}-2ax+b=0$ menyinggung $y=x$ maka Diskriminan Persamaan Kuadrat persekutuan adalah nol.
$x^{2}+x^{2}-2ax+b=0$
$2x^{2}-2ax+b=0$
$\begin{align}
D & = 0 \\
b^{2}-4ac & = 0 \\
(-2a)^{2}-4(2)(b) & = 0 \\
4a^{2}-8b & = 0 \\
a^{2}-2b & = 0\ \cdots\ (2) \\
\end{align}$
Jika persamaan $(1)$ dan $(2)$ kita eliminasi maka;
$\begin{array}{c|c|cc}
a^{2}-b=4 & \\
a^{2}-2b=0 & (-) \\
\hline
b =4\ &\ a^{2}-b =4 \\
&\ a^{2}-4 =4 \\
&\ a^{2} =8 \\
a^{2}+b=12
\end{array} $
$ \therefore $ Pilihan yang sesuai adalah $(A)\ 12$
22. Soal UN Matematika IPA 2016 🔗]
Persamaan garis singgung lingkaran $x^{2}+y^{2}-6x+4y-12=0$ di titik $(7,-5)$ adalah...
Alternatif Pembahasan:
Persamaan garis singgung Lingkaran $x^{2}+y^{2}+Ax+By+C=0$ di titik $\left ( x_{1},y_{1} \right )$ adalah;
$xx_{1}+yy_{1}+\frac{1}{2}Ax+\frac{1}{2}Ax_{1}+\frac{1}{2}By+\frac{1}{2}By_{1}+C=0$
Persamaan garis singgung untuk lingkaran $x^{2}+y^{2}-6x+4y-12=0$ di titik $(7,-5)$ adalah
$x(7)+y(-5)+\frac{1}{2}(-6)x+\frac{1}{2}(-6)(7)+\frac{1}{2}(4)y+\frac{1}{2}(4)(-5)-12=0$
$7x-5y-3x-21+2y-10-12=0$
$4x-3y=43$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ 4x-3y=43$
23. Soal UMB-PT 2013 Kode 172 🔗]
Jika pada lingkaran $L:x^{2}+y^{2}+2x-4y+3=0$ dibuat garis singgung $g$ di titik $(0,1)$ dan garis singgung $h$ di titik $(0,3)$, maka garis $g$ dan $h$ berpotongan di titik...
Alternatif Pembahasan:
Garis singgung lingkaran $x^{2}+y^{2}+2x-4y+3=0$ di titik $(0,1)$ adalah:
$x(0) +y(1)+\frac{1}{2}(2)(x+0)+\frac{1}{2}(-4)(y+(1))+3=0$
$y +x-2y-2+3=0$
$ x-y =-1$
Garis singgung lingkaran $x^{2}+y^{2}+2x-4y+3=0$ di titik $(0,3)$ adalah:
$x(0) +y(3)+\frac{1}{2}(2)(x+0)+\frac{1}{2}(-4)(y+(3))+3=0$
$3y +x-2y-6+3=0$
$ x+y =3$
Titik potong garis $g$ dan $h$ adalah:
$\begin{array}{c|c|cc}
x-y=-1 & \\
x+y =3 & (+) \\
\hline
2x =2 & \\
x =1 & \\
y=2
\end{array} $
$ \therefore $ Pilihan yang sesuai adalah $(E)\ (1,2)$
24. Soal SBMPTN 2017 Kode 106 🔗]
Diketahui suatu lingkaran kecil dengan radius $3\sqrt{2}$ melalui pusat suatu lingkaran besar yang mempunyai radius $6$. Ruas garis yang menghubungkan dua titik potong lingkaran merupakan diameter dari lingkaran kecil, seperti pada gambar. Luas daerah irisan kedua lingkaran adalah ...
Alternatif Pembahasan:
Luas daerah irisan kedua lingkaran jika kita arsir kurang lebih gambarnya menjadi sebagai berikut;
![Soal dan Pembahasan SBMPTN 2017 Matematika [Kode106] Soal dan Pembahasan SBMPTN 2017 Matematika [Kode106]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhpHlaIHeXcidn5ihlMg_Zyz9oyzvnMIuRFcC0iZdHvxWEGZ8T3ECZ0R6YnumULMwi8kG-hSUky33p94xN1Ho85H6VX3epMtyuDLsHj_4fR5yxWpsx7EZoe8taCchjNCrddf7akJf4E9k2l/s600/Lingkaran+Soal+SBMPTN+Luas+Arsiran.png)
Pada soal diberitahu ruas garis yang menghubungkan dua titik potong lingkaran merupakan diameter dari lingkaran kecil, sehingga gambar dapat kita sajikan seperti berikut;
![Luas Arsiran Soal dan Pembahasan SBMPTN 2017 Matematika [Kode106]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh3Q463Lh1EF0LSChAXD7BxgYAkExZyIhAmIAeLmSyhp4XTOQS_0_NoqVJP8tPAml9YthKFLgamgcHLk_ThsPqoMCxdrAMhd7i3A6YgXCZMUbj1uEw9MP8AnbjygQz3azxJCk7bo-NgumKR/s600/Lingkaran+Soal+SBMPTN+Luas+Arsiran+2.png)
Dari gambar diatas luas irisan lingkaran adalah luas daerah biru ditambah luas daerah kuning. Kita dapat menghitung luas daerah biru yang merupakan luas setengah lingkaran kecil karena $AC$ merupakan diameter lingkaran kecil.
$\begin{split}
L_{Biru} & = \dfrac{1}{2} \pi r^{2} \\
& = \dfrac{1}{2} \pi (3\sqrt{2})^{2} = \dfrac{1}{2} \pi (18)\\
& = 9 \pi
\end{split}$
Untuk menghitung luas daerah kuning yang merupakan luas tembereng lingkaran yang besar, dapat digunakan dengan menghitung selisih luas juring $ABC$ dengan luas segitiga $ABC$.
![Soal dan Pembahasan SBMPTN 2017 Matematika [Kode106] Soal dan Pembahasan SBMPTN 2017 Matematika [Kode106]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhyBWyCFi__WnlhY546KIxLLlogaywO24Iy4LWkA2UzceV6exEV5rvFZmBtHJOVN-xTsMXUNtY025HCxAKTpGCkLYrbdFOsK5Ue2BqkvuFR_HjW_qaYoIsQyXilMdq_WCrUYl9ZsShyphenhyphenEmZX/s600/Lingkaran+Soal+SBMPTN+Luas+Arsiran+3.png)
Karena $AC$ merupakan diameter sehingga $\measuredangle ABC=90^{\circ}$, sehingga;
$\begin{split}
L_{Juring\ ABC} & = \frac{90^{\circ}}{360^{\circ}} \pi r^{2} \\
& = \frac{1}{4} \pi (6)^{2} \\
& = \frac{1}{4} \pi 36 = 9 \pi
\end{split}$
$\begin{split}
L_{ABC} & = \frac{1}{2} 6 \cdot 6 \\
& = 18 \\
\hline
L_{Tembereng} & = 9 \pi - 18
\end{split}$
Luas irisan lingkaran adalah $ L_{Biru} +L_{Tembereng}$ yaitu $9 \pi +9 \pi - 18=18 \pi - 18$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 18\pi-18$
25. Soal UTBK-SBMPTN 2019 🔗
Persamaan lingkaran yang pusatnya terletak pada garis $2x+3y-5=0$ serta menyinggung sumbu $X$ negatif dan sumbu $Y$ positif adalah...
Alternatif Pembahasan:
Catatan calon guru tentang Lingkaran yang mungkin kita butuhkan adalah:
- Pusat $(a,b)$ dengan jari-jari $r$
$\Leftrightarrow $ Persamaan Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$ - Persamaan Umum Lingkaran $x^{2}+y^{2}+Ax+By+C=0$
$\Leftrightarrow $ Pusat $\left (-\frac{1}{2}A,-\frac{1}{2}B \right )$ dengan jari-jari $r=\sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C}$

Dari gambar di atas, dapat kita misalkan pusat lingkaran adalah $(-a,a)$ dan jari-jari $a$. Karena garis $2x+3y-5=0$ melalui pusat lingkaran $(-a,a)$ sehingga berlaku:
$\begin{align}
2x+3y-5 &= 0 \\
2(-a)+3(a)-5 &= 0 \\
a &= 5 \\
\hline
(x-a)^{2}+(y-b)^{2} &=r^{2} \\
(x+a)^{2}+(y-a)^{2} &=5^{2} \\
(x+5)^{2}+(y-5)^{2} &=5^{2} \\
x^{2}+10x+25+y^{2}-10y+25 &=25 \\
x^{2}+y^{2}+10x-10y+25 &=0
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ x^{2}+y^{2}+10x-10y+25=0$
26. Soal UTBK-SBMPTN 2019 🔗
Sebuah lingkaran memiliki pusat $(a,b)$ dengan jari-jari $12$ dan menyinggung garis $3x+4y=5$. Nilai $3a+4b$ yang mungkin adalah...
Alternatif Pembahasan:
Catatan calon guru tentang Lingkaran yang mungkin kita butuhkan adalah:
- Pusat $(a,b)$ dengan jari-jari $r$
$\Leftrightarrow $ Persamaan Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$ - Jarak titik $(x_{1},y_{1})$ ke garis $ax+by+c=0$ adalah:
$d=\left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right|$
Lingkaran dengan pusat $(a,b)$ dengan jari-jari $12$ menyinggung garis $3x+4y-5=0$, sehingga jarak titik pusat $(a,b)$ ke garis $3x+4y-5=0$ adalah jari-jari lingkaran $r=12$, sehingga berlaku:
$\begin{align}
d &=\left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\
12 &=\left| \dfrac{3a+4b-5}{\sqrt{3^{2}+4^{2}}} \right| \\
12 &=\left| \dfrac{3a+4b-5}{5} \right| \\
\hline
12 &= \dfrac{3a+4b-5}{5} \\
60 &= 3a+4b-5 \\
65 &= 3a+4b \\
\hline
-12 &= \dfrac{3a+4b-5}{5} \\
-60 &= 3a+4b-5 \\
-55 &= 3a+4b \\
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ -55\ \text{dan}\ 65$
27. Soal UTBK-SBMPTN 2019 🔗
Diketahui titk $P(4,a)$ dan lingkaran $L:x^{2}+y^{2}-8x-2y+1=0$. Jika titik $P$ berada dalam lingkaran $L$, maka nilai $a$ yang mungkin adalah...
Alternatif Pembahasan:
Catatan calon guru tentang Lingkaran yang mungkin kita butuhkan adalah:
Hubungan Titik $A(p,q)$ Pada lingkaran $L:x^{2}+y^{2}+Ax+By+C=0$
- Jika nilai $K=p^{2}+q^{2}+Ap+Bq+C$ dan $K \gt 0$ maka titik $A$ di luar $L$;
- Jika nilai $K=p^{2}+q^{2}+Ap+Bq+C$ dan $K = 0$ maka titik $A$ tepat pada $L$;
- Jika nilai $K=p^{2}+q^{2}+Ap+Bq+C$ dan $K \lt 0$ maka titik $A$ di dalam $L$;
Karena titik $P(4,a)$ dalam lingkaran $L:x^{2}+y^{2}-8x-2y+1=0$, maka berlaku:
$\begin{align}
4^{2}+a^{2}-8(4)-2(a)+1 & \lt 0 \\
16+a^{2}-32-2a+1 & \lt 0 \\
a^{2} -2a-15 & \lt 0 \\
(a+3)(a-5) & \lt 0
\end{align}$
Dengan menggunakan cara alternatif pertidaksamaan kuadrat, nilai $a$ yang memenuhi adalah $-3 \lt a \lt 5$.
$ \therefore $ Pilihan yang sesuai adalah $(B)\ -3 \lt a \lt 5$
28. Soal UTBK-SBMPTN 2019 🔗
Jika garis $y=mx+b$ menyinggung lingkaran $x^{2}+y^{2}=1$, maka nilai $b^{2}-m^{2}+1=\cdots$
Alternatif Pembahasan:
Catatan calon guru tentang Lingkaran yang mungkin kita butuhkan adalah:
- Jika nilai $D \gt 0$ maka garis memotong lingkaran;
- Jika nilai $D = 0$ maka garis menyinggung lingkaran;
- Jika nilai $D \lt 0$ maka garis tidak memotong dan tidak menyinggung lingkaran;
Karena garis $y=mx+b$ menyinggung lingkaran $x^{2}+y^{2}=1$, maka berlaku:
$\begin{align}
x^{2}+y^{2} & = 1 \\
x^{2}+(mx+b)^{2} & = 1 \\
x^{2}+ m^{2}x^{2}+2bmx+b^{2} & = 1 \\
\left(1+ m^{2} \right) x^{2}+2bmx+b^{2}-1 & = 0 \\
\hline
b^{2}-4ac & = 0 \\
\left( 2bm \right)^{2}-4\left(m^{2}+1 \right)\left(b^{2}-1 \right) & = 0 \\
4b^{2}m^{2}-4 m^{2} b^{2}-4b^{2}+4m^{2}+4 & = 0 \\
-4\left( b^{2}-m^{2}-1 \right)& = 0 \\
b^{2}-m^{2}-1 & = 0 \\
b^{2}-m^{2}-1+2 & = 0+2 \\
b^{2}-m^{2}+1 & = 2 \\
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 2$
29. Soal UTBK-SBMPTN 2019 🔗
Jika lingkaran $x^{2}+y^{2}=1$ menyinggung garis $ax+by=2b$, maka $\dfrac{a^{2}}{a^{2}+b^{2}}=\cdots$
Alternatif Pembahasan:
Catatan calon guru tentang Lingkaran yang mungkin kita butuhkan adalah:
- Jika nilai $D \gt 0$ maka garis memotong lingkaran;
- Jika nilai $D = 0$ maka garis menyinggung lingkaran;
- Jika nilai $D \lt 0$ maka garis tidak memotong dan tidak menyinggung lingkaran;
Karena garis $y=2-\dfrac{ax}{b}$ menyinggung lingkaran $x^{2}+y^{2}=1$, maka berlaku:
$\begin{align}
x^{2}+y^{2} & = 1 \\
x^{2}+\left( 2-\dfrac{ax}{b} \right)^{2} & = 1 \\
x^{2}+4+ \dfrac{a^{2}x^{2}}{b^{2}} - \dfrac{4ax}{b} & = 1 \\
\left( \dfrac{a^{2}}{b^{2}}+1 \right) x^{2} - \dfrac{4a}{b}x + 3 & = 0 \\
\hline
D & = 0 \\
b^{2}-4ac & = 0 \\
\left( \dfrac{4a}{b} \right)^{2}-4\left( \dfrac{a^{2}}{b^{2}}+1 \right)\left( 3 \right) & = 0 \\
\dfrac{16a^{2}}{b^{2}} -12 \left( \dfrac{a^{2}+b^{2}}{b^{2}} \right) & = 0 \\
\dfrac{16a^{2}-12b^{2}-12a^{2}}{b^{2}} & = 0 \\
4a^{2}-12b^{2} & = 0 \\
a^{2} & = 3b^{2}\\
\hline
\dfrac{a^{2}}{a^{2}+b^{2}} & = \dfrac{3b^{2}}{3b^{2}+b^{2}} \\
& = \dfrac{3b^{2}}{4b^{2}} = \dfrac{3 }{4}
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ \frac{3}{4}$
30. Soal UTBK-SBMPTN 2019 🔗
Salah satu persamaan garis singgung lingkaran $x^{2}+y^{2}-4x+2y=0 $ yang tegak lurus dengan garis $x+2y=5$ adalah...
Alternatif Pembahasan:
Catatan calon guru tentang Lingkaran yang mungkin kita butuhkan adalah:
Jika diketahui gradien garis singgung lingkaran $(m)$
- Persamaan Lingkaran $x^{2}+y^{2}=r^{2}$
$\Leftrightarrow $ PGS: $y=mx\pm r\sqrt{m^{2}+1}$ - Persamaan Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$
$\Leftrightarrow $ PGS: $y-b=m(x-a)\pm r\sqrt{m^{2}+1}$
Karena garis singgung lingkaran $x^{2}+y^{2}-4x+2y=0 $ tegak lurus dengan garis $x+2y=5$ ($m=-\dfrac{1}{2}$), maka gradien garis singgung lingkaran adalah $m_{1} \cdot \left( -\dfrac{1}{2} \right) =-1\ \Leftrightarrow m_{1}=2$.
$\begin{align}
x^{2}+y^{2}-4x+2y &= 0 \\
x^{2}-4x+y^{2}+2y &= 0 \\
(x-2)^{2}-4+(y+1)^{2}-1 &= 0 \\
(x-2)^{2} +(y+1)^{2} &= 5
\end{align}$
Persamaan garis singgung lingkaran dengan $m=2$ adalah:
$\begin{align}
y-b & = m(x-a)\pm r\sqrt{m^{2}+1} \\
y+1 & = 2(x-2)\pm \sqrt{5} \sqrt{2^{2}+1} \\
y+1 & = 2 x-4 \pm 5 \\
y & = 2 x-5 \pm 5 \\
\hline
y & = 2 x-5 - 5 \\
y & = 2 x-5 + 5 \\
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ y=2x-10$
31. Soal UTBK-SBMPTN 2019 🔗
Sebuah lingkaran memiliki pusat $(a,b)$ dengan $a,b \gt 3$, menyinggung garis $3x+4y=12$. Jika lingkaran tersebut berjari-jari $12$, maka $3a+4b=\cdots$
Alternatif Pembahasan:
Catatan calon guru tentang Lingkaran yang mungkin kita butuhkan adalah:
- Pusat $(a,b)$ dengan jari-jari $r$
$\Leftrightarrow $ Persamaan Lingkaran $(x-a)^{2}+(y-b)^{2}=r^{2}$ - Jarak titik $(x_{1},y_{1})$ ke garis $ax+by+c=0$ adalah:
$d=\left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right|$
Lingkaran dengan pusat $(a,b)$ dengan jari-jari $12$ menyinggung garis $3x+4y-12=0$, sehingga jarak titik pusat $(a,b)$ ke garis $3x+4y-12=0$ adalah jari-jari lingkaran $r=12$, sehingga berlaku:
$\begin{align}
d &=\left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\
12 &=\left| \dfrac{3a+4b-12}{\sqrt{3^{2}+4^{2}}} \right| \\
12 &=\left| \dfrac{3a+4b-12}{5} \right| \\
\end{align}$
Karena $a,b \gt 3$ maka $3a+4b-12 \gt 0$, sehingga berlaku:
$\begin{align}
12 &= \dfrac{3a+4b-12}{5} \\
60 &= 3a+4b-12 \\
72 &= 3a+4b
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(E)\ 72$
32. Soal UM UGM 2014 Kode 531/532 🔗
Jika garis $y=mx+k$ menyinggung lingkaran $x^{2}+y^{2}-10x+6y+24=0$ di titik $(8,-4)$, maka nilai $m+k$ adalah...
Alternatif Pembahasan:
Lingkaran $x^{2}+y^{2}-10x+6y+24=0$ bersinggungan dengan garis $y=mx+k$ di titik $(8,-4)$ maka jari-jari lingkaran merupakan jarak titik pusat $(5,-3)$ ke garis $y=mx+k$, sehingga berlaku:
$\begin{align}
\sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} & = \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\
\sqrt{\frac{1}{4}(-10)^{2}+\frac{1}{4}(6)^{2}-24} & = \left| \dfrac{(m)(5)+(-1)(-3)+k}{\sqrt{(m)^{2}+(-1)^{2}}} \right| \\
\sqrt{25+9-24} & = \left| \dfrac{5m+3+k}{\sqrt{(m^{2}+1}} \right| \\
\sqrt{10} & = \left| \dfrac{5m+3+k}{\sqrt{(m^{2}+1}} \right| \\
\sqrt{10m^{2}+10} & = 5m+3+k
\end{align}$
Garis $y=mx+k$ melalui titik $(8,-4)$ sehingga $-4=8m+k$ atau $k=-4-8m$,
$\begin{align}
\sqrt{10m^{2}+10} & = 5m+3+k\\
\sqrt{10m^{2}+10} & = 5m+3-4-8m\\
\sqrt{10m^{2}+10} & = -1-3m\\
10m^{2}+10 & = \left( -1-3m \right)^{2}\\
10m^{2}+10 & = 9m^{2}+6m+1 \\
m^{2}-6m+9 & = 0 \\
\left( m-3 \right)^{2} & = 0 \\
m & = 3
\end{align}$
Untuk $m=3$ kita peroleh $k=-4-8m=-4-8(3)=-28$, sehingga nilai $m+k=3-28=-25$
$ \therefore $ Pilihan yang sesuai adalah $(B)\ -25$
33. Soal UM UGM 2019 Kode 624 🔗
Bilangan $A \gt 0$ sehingga lingkaran $x^{2}+y^{2}+2x-4Ay+40=0$ mempunyai jari-jari $A+1$ adalah...
Alternatif Pembahasan:
Lingkaran $x^{2}+y^{2}+2x-4Ay+40=0$ jari-jarinya adalah $A+1$ sehingga dapat kita tuliskan:
$\begin{align}
r &= \sqrt{\frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C} \\
A+1 &=\sqrt{ \frac{1}{4}(2)^{2}+\frac{1}{4}(-4A)^{2}-40 }\\
\left( A+1 \right)^{2} &= \frac{1}{4}(2)^{2}+\frac{1}{4}(-4A)^{2}-40 \\
A^{2}+2A+1 &= 1+4A^{2}-40 \\
0 &= 3A^{2}-2A-40 \\
0 &= \left ( 3A+10 \right ) \left ( A-4 \right )\\
& A=-\frac{10}{3}\ \text{atau}\ A=4
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(B)\ 4$
34. Soal UM-UGM 2018 Kode 576 🔗
Diberikan lingkaran pada bidang koordinat yang memotong sumbu-$x$ di $\left( 1,0 \right)$ dan $\left( 3,0 \right)$. Jika lingkaran tersebut menyingung sumbu-$y$, maka titik singgung yang mungkin adalah...
Alternatif Pembahasan:
Lingkaran $x^{2}+y^{2}+Ax+By+C=0$ melalui titik $\left( 1,0 \right)$, $\left( 3,0 \right)$ dan menyinggung sumby-$y$ kita misalkan di titik $\left( 0,p \right)$, sehingga dapat kita tuliskan:
- Lingkaran melalui titik $ \left( 1,0 \right)$, kita peroleh $( 1)^{2}+(0)^{2}+A( 1)+B(0)+C= 0$ sehingga $ A +C =-1$
- Lingkaran melalui titik $ \left( 3,0 \right)$, kita peroleh $(3)^{2}+(0)^{2}+A(3)+B(0)+C= 0$ sehingga $3A +C =-9$
- Lingkaran melalui titik $\left( 0,p \right)$, kita peroleh $(0)^{2}+(p)^{2}+A(0)+B(p)+C= 0$ sehingga $ p^{2}+Bp+C=0$
Dengan proses eliminasi atau substitusi pada persamaan $ A +C =-1$, dan $3A +C =-9$ kita peroleh:
$\begin{array}{c|c|cc}
A+C=-1 & \\
3A+C=-9 & (-) \\
\hline
2A = -8\ & \\
A = -4 & C=3
\end{array} $
Untuk $A=-4$ dan $C=3$ kita peroleh lingkaran $x^{2}+y^{2}-4x+By+3=0$. Lingkaran menyinggung sumbu-$y$ di $\left( 0,p \right)$ sehingga pusatnya adalah $\left( 2,p \right)$ dan $r= 2$.
Jika kita gambarkan keadaan lingkarannya seperti berikut ini:

Dari pusat lingkaran $\left( 2,p \right)$ maka $-\frac{1}{2}B=p$ atau $B=-2p$, dan untuk jari-jari $r= 2$ sehingga dapat kita tuliskan:
$\begin{align}
r &= \sqrt{ \dfrac{1}{4}A^{2} + \dfrac{1}{4}B^{2}- C } \\
2 &= \sqrt{ \dfrac{1}{4}(-4)^{2} + \dfrac{1}{4}(-2p)^{2}-3 } \\
4 &= 4 + p^{2} - 3 \\
p^{2} &= 3 \rightarrow p=\pm \sqrt{3}
\end{align}$
titik potong terhadap sumbu-$y$ adalah $\left( 0, \sqrt{3} \right)$ dan $\left( 0, -\sqrt{3} \right)$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ \left( 0,\sqrt{3} \right)$
35. Soal UM-UGM 2018 Kode 276 🔗
Diberikan garis $y=\dfrac{x}{3}$ dan $y=3x$. Persamaan lingkaran yang menyinggung dua garis tersebut, berpusat di $\left( -a,-a \right)$, $a \gt 0$, dan berjari-jari $\dfrac{6}{\sqrt{10}}$ adalah...
Alternatif Pembahasan:
Lingkaran yang menyinggung garis $y=\dfrac{x}{3}$ dan $y=3x$ memiliki jari-jari $r=\dfrac{6}{\sqrt{10}}$ sehingga jarak titik pusat $\left( -a,-a \right)$ ke garis $ y=3x$ adalah $\dfrac{6}{\sqrt{10}}$.
$\begin{align} d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\ r &= \left| \dfrac{(-3)(-a)+(1)(-a)+(0)}{\sqrt{(-3)^{2}+(1)^{2}}} \right| \\ \dfrac{6}{\sqrt{10}} &= \left| \dfrac{3a-a}{\sqrt{10}} \right| \\ \dfrac{6}{\sqrt{10}} &= \left| \dfrac{2a}{\sqrt{10}} \right| \\ a &= \pm 3 \end{align}$
Nilai $a \gt 0$, nilai $a=3$ sehingga pusat lingkaran adalah $\left( -3,-3 \right)$ dan dengan $r=\dfrac{6}{\sqrt{10}}$ persamaan lingkaran adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x+3 \right)^{2}+\left( y+3 \right)^{2} &= \left( \frac{6}{\sqrt{10}} \right)^{2} \\
x^{2}+6x+9+y^{2}+6y+9 &= \dfrac{36}{10} \\
x^{2} +y^{2}+6x +6y+18- \dfrac{36}{10}&= 0 \\
x^{2}+y^{2}+6x+6y+\frac{72}{5} &= 0
\end{align}$
Jika kita gambarkan keadaan lingkaran dan garisnya seperti berikut ini:

$ \therefore $ Pilihan yang sesuai adalah $(A)\ x^{2}+y^{2}+6x+6y+\frac{72}{5}=0$
36. Soal UM-UGM 2017 Kode 714 🔗
Titik pusat lingkaran $L$ terletak di kuadran I dan terletak pada garis $y=2x+1$. Jika lingkaran $L$ menyinggung sumbu $Y$ di titik $\left( 0,11 \right)$ maka persamaan lingkaran L adalah...
Alternatif Pembahasan:
Lingkaran L yang menyinggung sumbu-$y$ di titik $\left( 0,11 \right)$ sehingga titik pusatnya dapat kita misalkan adalah $\left( p,11 \right)$ dan jari-jari $r=p$. Karena titik pusat berada di garis $y=2x+1$ maka berlaku $11=2p+1$ atau $p=5$.
Dengan titik pusat lingkaran L adalah $\left( 5,11 \right)$ dan jari-jari $r=5$ persamaan lingkaran adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x-5 \right)^{2}+\left( y-11 \right)^{2} &= 5^{2} \\
x^{2}-10x+25+y^{2}-22y+121 &= 25 \\
x^{2} +y^{2}-10x-22y+ 121 &= 0
\end{align}$
Jika kita gambarkan keadaan lingkaran dan garisnya seperti berikut ini:

$ \therefore $ Pilihan yang sesuai adalah $(C)\ x^{2}+y^{2}-10x-22y+121=0$
37. Soal UM-UGM 2017 Kode 738 🔗
Sebuah lingkaran dengan pusat $P \left( 2,3 \right)$ dan menyinggung garis $4x+3y -7 = 0$, maka persamaan lingkaran ialah...
Alternatif Pembahasan:
Lingkaran yang berpusat di $P \left( 2,3 \right)$ dan meyinggung garis garis $4x+3y -7 = 0$, maka jari-jari lingkaran dapat kita tentukan dengan menghitung jarak titik pusat $P \left( 2,3 \right)$ ke garis $4x+3y -7 = 0$.
$\begin{align} d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\ r &= \left| \dfrac{(4)(2)+(3)(3)+(-7)}{\sqrt{(4)^{2}+(3)^{2}}} \right| \\ &= \left| \dfrac{10}{\sqrt{16+9}} \right|= \left| \dfrac{10}{5} \right|= 2 \end{align}$
Lingkaran pusatnya $P \left( 2,3 \right)$ dan $r=2$, maka persamaanya adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x-2 \right)^{2}+\left( y-3 \right)^{2} &= 4
\end{align}$
Jika kita gambarkan Lingkaran yang menyinggung garis, seperti berikut ini:

$ \therefore $ Pilihan yang sesuai adalah $(A)\ \left( x-2 \right)^{2}+\left( y-3 \right)^{2} = 4$
38. Soal UM-UGM 2016 Kode 582 🔗
Diketahui $\left( 1,p \right)$ berada pada lingkaran $x^{2}+y^{2}-2y=0$. Persamaan lingkaran dengan pusat $\left( 1,p \right)$ dan menyinggung garis $px+y=4$ adalah...
Alternatif Pembahasan:
Titik $\left( 1,p \right)$ berada pada lingkaran $x^{2}+y^{2}-2y=0$ sehingga dapat kita tuliskan
$\begin{align} x^{2}+y^{2}-2y &= 0 \\ 1^{2}+p^{2}-2p &= 0 \\ p^{2}-2p+1 &= 0 \\ p^{2}-2p+1 &= 0 \\ \left( p-1 \right)\left( p-1 \right) &= 0 \\ p=1 & \end{align}$
Untuk $p=1$ kita peroleh pusat lingkaran $\left( 1,1 \right)$ yang menyinggung garis $x+y=4$ jari-jarinya adalah jarak titik pusat $ \left( 1,1 \right)$ ke garis $x+y = 4$.
$\begin{align} d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\ r &= \left| \dfrac{(1)(1)+(1)(1)+(-4)}{\sqrt{(1)^{2}+(1)^{2}}} \right| \\ &= \left| \dfrac{-2}{\sqrt{1+1}} \right|= \dfrac{2}{\sqrt{2}} \end{align}$
Lingkaran pusatnya $\left( 1,1 \right)$ dan $r=\dfrac{2}{\sqrt{2}}$, maka persamaanya adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x-1 \right)^{2}+\left( y-1 \right)^{2} &= \left( \dfrac{2}{\sqrt{2}} \right)^{2} \\
x^{2}-2x+1+y^{2}-2y+1 &= 2 \\
x^{2} +y^{2}-2x -2y &= 0
\end{align}$
Jika kita gambarkan Lingkaran yang menyinggung garis, seperti berikut ini:

$ \therefore $ Pilihan yang sesuai adalah $(C)\ x^{2}+y^{2}-2x-2y=0$
39. Soal UM UNDIP 2019 Kode 324 🔗
Persamaan lingkaran lingkaran yang berpusat di titik $P\left( -2,3 \right)$ dan menyinggung garis $4x-3y +2 = 0$ mempunyai persamaan...
Alternatif Pembahasan:
Lingkaran yang berpusat di $P \left( -2,3 \right)$ dan meyinggung garis garis $4x-3y +2 = 0$, maka jari-jari lingkaran dapat kita tentukan dengan menghitung jarak titik pusat $P \left( -2,3 \right)$ ke garis $4x-3y +2 = 0$.
$\begin{align} d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\ r &= \left| \dfrac{(4)(-2)+(-3)(3)+(2)}{\sqrt{(4)^{2}+(-3)^{2}}} \right| \\ &= \left| \dfrac{-15}{\sqrt{16+9}} \right|= \left| \dfrac{-15}{5} \right|= 3 \end{align}$
Lingkaran pusatnya $P \left( 2,3 \right)$ dan $r=2$, maka persamaanya adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x+2 \right)^{2}+\left( y-3 \right)^{2} &= (3)^{2} \\
x^{2}+4x+4+y^{2}-6y+9 &= 9 \\
x^{2}+y^{2}+4x-6y+4 &= 0 \\
\end{align}$
Jika kita gambarkan Lingkaran yang menyinggung garis, seperti berikut ini:

$ \therefore $ Pilihan yang sesuai adalah $(C)\ x^{2}+y^{2}+4x-6y+4=0$
40. Soal UM UNDIP 2018 Kode 730 🔗
Lingkaran yang sepusat dengan lingkaran $x^{2}+y^{2}-6x+4y-13=0$ dan menyinggung garis $3x+4y+9=0$ mempunyai persamaan...
Alternatif Pembahasan:
Pusat lingkaran $x^{2}+y^{2}-6x+4y-13=0$ adalah $\left( -\frac{1}{2}A, -\frac{1}{2}B \right)= \left( 3,-2 \right)$.
Lingkaran dengan titik pusat $\left( 3,-2 \right)$ dan menyinggung garis garis $3x+4y+9=0$, maka jari-jari lingkaran dapat kita tentukan dengan menghitung jarak titik pusat $\left( 3,-2 \right)$ ke garis $3x+4y+9=0$.
$\begin{align} d &= \left| \dfrac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}} \right| \\ r &= \left| \dfrac{(3)(3)+(4)(-2)+(9)}{\sqrt{(3)^{2}+(4)^{2}}} \right| \\ &= \left| \dfrac{10}{\sqrt{9+16}} \right|= \left| \dfrac{10}{5} \right|= 2 \end{align}$
Lingkaran pusatnya $\left( 3,-2 \right)$ dan $r=2$, maka persamaanya adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x-3 \right)^{2}+\left( y+2 \right)^{2} &= (2)^{2} \\
x^{2}-6x+9+ y^{2}+4y+4 &= 4 \\
x^{2}+y^{2}-6x+4y+9 &= 0 \\
\end{align}$
Jika kita gambarkan Lingkaran yang menyinggung garis, seperti berikut ini:

$ \therefore $ Pilihan yang sesuai adalah $(D)\ x^{2}+y^{2}-6x+4y+9=0$
41. Soal UM UGM 2019 Kode 923/924 🔗
Diberikan lingkaran pada bidang koordinat dengan titik pusat $\left(a,b \right)$ dan memotong sumbu-$X$ di titik $\left( 3,0 \right)$ dan $\left( 9,0 \right)$. Jika garis yang melalui titik $\left( 0,3 \right)$ menyinggung lingkaran di titik $\left( 3,0 \right)$, maka nilai dari $a^{2}-b^{2}$ adalah...
Alternatif Pembahasan:
Jika kita gambarkan lingkaran dan garis yang disebutkan oleh soal, seperti berikut ini:

Persamaan garis yang melalui titik $A\left( 0,3 \right)$ dan $B\left( 3,0 \right)$ adalah garis $AB$ yaitu:
\begin{align}
\dfrac{x-x_{1}}{x_{2}-x_{1}} &= \dfrac{y-y_{1}}{y_{2}-y_{1}} \\
\dfrac{x-0}{3-0} &= \dfrac{y-3}{0-3} \\
-3x &= 3y-9 \\
-3x &= 3y-9 \\
y &= 3-x
\end{align}
Garis $AB$ menyinggung lingkaran dan $BP$ merupakan jari-jari lingkaran sehingga $AB \perp BP$ dan kita peroleh:
\begin{align}
m_{AB} \cdot m_{BP} &= -1 \\
-1 \cdot \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}&= -1 \\
\dfrac{b-0}{a-3}&= 1 \\
b &= a-3
\end{align}
Jari-jari lingkaran $BP$ dan $PC$, sehingga berlaku:
\begin{align}
\left| BP \right| &= \left| PC \right| \\
\sqrt{ \left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2}} &= \sqrt{ \left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2}} \\
\left( a-3 \right)^{2}+\left( b-0 \right)^{2} &= \left( a- 9 \right)^{2}+\left( b- 0 \right)^{2} \\
\left( a-3 \right)^{2} &= \left( a- 9 \right)^{2} \\
a^{2}-6a+9 &= a^{2}-18a+81 \\
12a &= 72 \\
a &= 6 \rightarrow b= 3 \\
\hline
a^{2}-b^{2} &= 36-9=27
\end{align}
$\therefore$ Pilihan yang sesuai $(C)\ 27$
42. Soal SBMPTN 2016 Kode 249🔗
Diketahui persegi dengan panjang sisi $12$ dan setengah lingkaran dengan diameter pada alas, seperti pada gambar. Garis $CE$ menyinggung lingkaran di titik $F$. Panjang garis $CE$ adalah...
Alternatif Pembahasan:
Dari informasi pada soal, jika kita misalkan $EA=x$ maka kita peroleh $ED=12-x$ dan unsur lain dapat kita gambarkan seperti berikut ini:
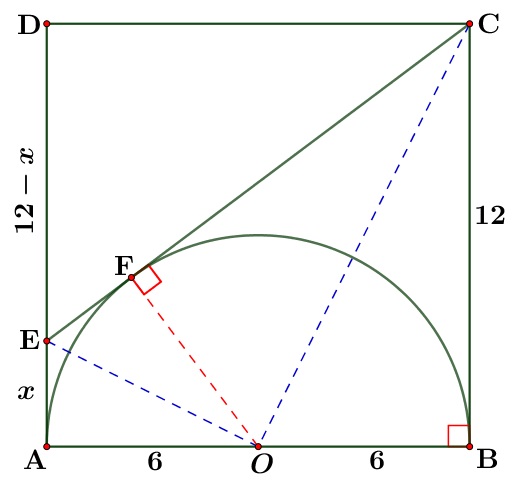
Dari gambar di atas kita peroleh bahwa $\bigtriangleup OBC$ kongruen dengan $\bigtriangleup OCF$ sehingga dengan $BC=12$ kita peroleh $CF=12$.
Begitu juga dengan $\bigtriangleup AOE$ kongruen dengan $\bigtriangleup OEF$ sehingga sehingga dengan $AE=x$ kita peroleh $EF=x$
Dari segitiga siku-siku $ECD$ kita peroleh:
$\begin{align}
EC^{2} & = ED^{2}+CD^{2} \\
\left( EF+FC \right)^{2} & = ED^{2}+CD^{2} \\
\left( x+12 \right)^{2} & = \left( 12-x \right)^{2}+12^{2} \\
x^{2}+24x+144 & = x^{2}-24x+144+144 \\
24x & = -24x+144 \\
24x+24x & = 144 \\
48x & = 144\ \\
x & = \dfrac{144}{48}=3
\end{align}$
Untuk $x=3$ kita peroleh $EC=x+12=3+12=15$.
$\therefore$ Pilihan yang sesuai adalah $(C)\ 15$
44. Contoh Soal TKA Matematika SMA🔗
Diketahui persamaan lingkaran $x^{2}+y^{2}-6x-2y-26=0$.
Di antara lima pernyataan berikut, tentukan pernyataan yang benar!.
- Lingkaran tersebut berpusat di $(1, 3)$.
- Panjang jari-jari lingkaran tersebut $6$ satuan panjang.
- Jarak pusat lingkaran dengan sumbu-$x$ adalah $3$.
- Jarak pusat lingkaran dengan sumbu-y adalah $1$.
- Garis $y=0$ memotong lingkaran di dua titik.
Alternatif Pembahasan:
Dari informasi persamaan lingkaran $x^{2}+y^{2}-6x-2y-26=0$ pada soal, kita coba tentukan kebenaran pernyataan yang diberikan.
- Lingkaran tersebut berpusat di $(1, 3)$. (Salah)
$\begin{align}
\text{Pusat}\ &= \left (-\dfrac{1}{2}A,-\dfrac{1}{2}B \right ) \\ &= \left(-\dfrac{1}{2}(-6),-\dfrac{1}{2}(-2) \right ) \\ &= \left( 3, 1 \right)
\end{align}$
atau $\begin{align}
x^{2}+y^{2}-6x-2y-26 &= 0 \\ x^{2}-6x+y^{2}-2y &= 26 \\ \left( x-3 \right)^{2}-9 + \left( y-1 \right)^{2}-1 &= 26 \\ \left( x-3 \right)^{2} + \left( y-1 \right)^{2} &= 26+10 \\ \left( x-3 \right)^{2} + \left( y-1 \right)^{2} &= 6^{2} \end{align}$ - Panjang jari-jari lingkaran tersebut $6$ satuan panjang. (Benar)
- Jarak pusat lingkaran dengan sumbu-$x$ adalah $3$. (Salah)
karena jarak pusat lingkaran ke sumbu-$x$ adalah $1$. - Jarak pusat lingkaran dengan sumbu-y adalah $1$. (Salah)
karena jarak pusat lingkaran ke sumbu-$y$ adalah $3$. - Garis $y=0$ memotong lingkaran di dua titik. (Benar)
$\begin{align}
x^{2}+y^{2}-6x-2y-26 &= 0 \\ x^{2}+0^{2}-6x-2(0)-26 &= 0 \\ x^{2}-6x-26 &= 0 \\ \hline D &= b^{2}-4ac \\ D &= 6^{2}-4(1)(26) \\ D &= 36-4(1)(-26) \\ D &= 36+104=140 \end{align}$
$D \gt 0$ memotong di dua titik yang berbeda
$\therefore$ Pilihan yang sesuai adalah $(D)$ Pernyataan $2$ dan $5$
44. Contoh Soal TKA Matematika SMA🔗
Persamaan lingkaran yang berpusat di $A\ (-2,1)$ dan menyinggung garis $4x+3y-20=0$ di titik $B\ (2,4)$ adalah....
Alternatif Pembahasan:
Lingkaran yang berpusat di $A\ (-2,1)$ dan meyinggung garis garis $4x+3y-20=0$, maka jari-jari lingkaran dapat kita tentukan dengan menghitung jarak titik pusat $A\ (-2,1)$ ke di titik $B\ (2,4)$.
$\begin{align} d &= \sqrt{ \left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2}} \\ r &= \sqrt{ \left(2+2 \right)^{2}+\left(4-1 \right)^{2}} \\ &= \sqrt{ 16+9} = 5 \end{align}$
Lingkaran pusatnya $A\ (-2,1)$ dan $r=5$, maka persamaanya adalah:
$\begin{align}
\left( x-a \right)^{2}+\left( y-b \right)^{2} &= r^{2} \\
\left( x+2 \right)^{2}+\left( y-1 \right)^{2} &= 25 \\
x^{2}+4x+4+y^{2}-2y+1 &= 25 \\
x^{2}+y^{2}+4x-2y-20 &= 0
\end{align}$
Jika kita gambarkan Lingkaran yang menyinggung garis, seperti berikut ini:

$ \therefore $ Pilihan yang sesuai adalah $(D)\ x^{2}+y^{2}+4x-2y-20=0$
Beberapa pembahasan soal Matematika Dasar Lingkaran di atas adalah coretan kreatif siswa pada:
- lembar jawaban penilaian harian matematika,
- lembar jawaban penilaian akhir semester matematika,
- presentasi hasil diskusi matematika atau
- pembahasan quiz matematika di kelas.
Catatan Soal dan Pembahasan Matematika Dasar SMA Lingkaran di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.
Ayo Share (Berbagi) Satu Hal Baik.
Jangan jadikan sekolah hanya untuk mencari nilai, tetapi bagaimana sekolah itu menjadikanmu bernilai.

com.png)


![Soal dan Pembahasan SBMPTN 2017 Matematika [Kode106] Soal dan Pembahasan SBMPTN 2017 Matematika [Kode106]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiMCfuIczlZYIbz2sEzz1wBuOcoWC_Cfc7-9lLA0Tb1JUXnWwaHRGAa_aqJfNQFb_qmLzwLWS863RHPSkFtifoLOQGFX41wji0FLCTEBH11ZtjfGs1PteNhprvSCfPuE23UFpfvnKgFAXko/s600/Lingkaran+Soal+SBMPTN.png)
