30+ Soal dan Pembahasan Matematika SMA Eksponen (Bilangan Berpangkat)

Calon guru belajar matematika dasar SMP lewat soal dan pembahasan Pola Bilangan, Barisan dan Deret pada matematika SMP. Apa yang diharapkan setelah mempelajari materi ini, yaitu dapat menyelesaikan masalah yang berkaitan dengan pola pada barisan bilangan dan barisan konfigurasi objek.

Soal matematika dasar Pola Bilangan, Barisan dan Deret untuk SMP ini kita pilih dari soal-soal yang sudah pernah diujikan pada soal Ujian Sekolah matematika SMP, soal Ujian Nasional matematika SMP, atau soal ujian seleksi akademik masuk SMA Unggulan atau SMA Favorit.

---

BILANGAN SEBAGAI BARISAN DAN DERET

Pola bilangan dapat dituliskan dalam dua bentuk, yaitu dalam barisan bilangan atau deret bilangan.

Jika $U_{n}$ adalah suku ke-$n$ dari suatu pola bilangan maka barisan bilangan $U_{n}$ dapat dituliskan dengan $U_{1},U_{2},U_{3},\cdots,U_{n}$.

Sedangkan deret bilangan dituliskan $U_{1}+U_{2}+U_{3}+\cdots+U_{n}$. Jika $S_{n}$ adalah jumlah $n$ suku pertama deret bilangan maka $S_{n}=U_{1}+U_{2}+U_{3}+\cdots+U_{n}$.

---

BARISAN DAN DERET BILANGAN

Berikut kita tuliskan beberapa barisan dan deret bilangan. Untuk nama barisan bilangan ini mungkin berbeda pada beberapa buku, tetapi pola barisan bilangan dan bentuk umum yang dimaksud adalah sama.

• Barisan Bilangan Asli: $1,2,3,4,\cdots$
  Pola: $1,2,3,4,\cdots$
  Suku ke-$n$: $U_{n}=n$
  Jumlah $n$ suku pertama: $S_{n}= \dfrac{1}{2} \left( n \right)\left( n+1 \right)$
• Barisan Bilangan Persegi: $1, 4, 9, 16, 25,\cdots$
  Pola: $1^{2},2^{2},3^{2},4^{2},\cdots$
  Suku ke-$n$: $U_{n}=n^{2}$
  Jumlah $n$ suku pertama: $S_{n}= \dfrac{1}{3} \left( n \right)\left( n+1 \right)\left( n+2 \right)$
• Barisan Bilangan Persegi panjang : $2, 6, 12, 20, 30,\cdots$
  Pola: $1 \times 2, 2\times 3,3 \times 4,4 \times 5,\cdots$
  Suku ke-$n$: $U_{n}=n \left( n+1 \right)$
  Jumlah $n$ suku pertama: $S_{n}= \dfrac{1}{3} \left( n \right)\left( n+1 \right)\left( n+2 \right)$
• Barisan Bilangan Segitiga: $1, 3, 6, 10, 15,\cdots$
  Pola: $1, 1 + 2, 1+2+3,1+2+3+4,\cdots$
  Suku ke-$n$: $U_{n}=\dfrac{1}{2} \left(n \right) \left( n+1 \right)$
  Jumlah $n$ suku pertama: $S_{n}= \dfrac{1}{6} \left( n \right)\left( n+1 \right) \left( n+2 \right)$
• Barisan Bilangan Kubik: $1, 8, 27, 64, 125,\cdots$
  Pola: $1^{3},2^{3},3^{3},4^{3},\cdots$
  Suku ke-$n$: $U_{n}=n^{3}$
  Jumlah $n$ suku pertama: $S_{n}= \left[\dfrac{1}{2} \left( n \right)\left( n+1 \right) \right]^{2}$
• Barisan Bilangan Balok: $6, 24, 60, 120 , 720,\cdots$
  Pola: $1 \times 2 \times 3, 2 \times 3 \times 4, 3 \times 4 \times 5, 4 \times 5 \times 6,\cdots$
  Suku ke-$n$: $U_{n}= \left(n \right) \left( n+1 \right) \left(n+2 \right)$
  Jumlah $n$ suku pertama: $S_{n}= \dfrac{1}{4} \left( n \right)\left( n+1 \right) \left( n+2 \right) \left( n+3 \right)$
• Barisan Bilangan Aritmetika: $3, 7, 11, 15, 19, 23, 27, 31, 35,\cdots$
  Pola: $a,\ a+b,\ a+2b,\ a+3b,\ \cdots$
  Suku ke-$n$: $U_{n}= a+\left( n-1 \right)$
  Jumlah $n$ suku pertama:
  $\begin{align} S_{n}\ &= \dfrac{n}{2} \left( 2a+(n-1)b \right) \\ &= \dfrac{n}{2} \left( a+a+(n-1)b \right) \\ S_{n}\ &= \dfrac{n}{2} \left( a+U_{n} \right) \end{align}$
• Barisan Bilangan Geometri: $3, 6, 12, 24, 48, 96, 192,\cdots$
  Pola: $a,\ a \cdot r^{1},\ a \cdot r^{2},\ a\cdot r^{3},\ \cdots$
  Suku ke-$n$: $U_{n}= a \cdot r^{n-1}$
  Jumlah $n$ suku pertama:
  $\begin{align} S_{n}\ &= \dfrac{n}{2} \left( 2a+(n-1)b \right) \\ &= \dfrac{n}{2} \left( a+a+(n-1)b \right) \\ S_{n}\ &= \dfrac{ a \left( r^{n} - 1 \right)}{\left(r-1 \right)},\ \text{dengan}\ r \neq 1 \end{align}$
• Barisan Bilangan Fibonacci: $1,1, 2, 3, 5, 8, 13,\cdots$
  Pola: Jumlah dua suku berurutan adalah suku berikutnya.

Ada banyak lagi jenis barisan atau deret bilangan yang belum kita tuliskan, untuk menambah pengetahuan kita terkait pola bilangan, barisan bilangan, atau deret bilangan mari kita lihat beberapa contoh soal berikut.

---

Pembahasan Soal Latihan Pola, Barisan, dan Deret Bilangan Matematika SMP

Soal latihan pola bilangan berikut ini, silahkan dikerjakan terlebih dahulu secara mandiri sebelum membuka buku atau sumber lain untuk melihat pembahasan soal. Setelah selesai silahkan Periksa Jawaban dan jika hasilnya belum memuaskan, pilih Ulangi Tes untuk tes ulang.

Ayo dicoba terlebih dahulu, Sebelum melihat pembahasan soal.
Tunjukkan Kemampuan Matematika Terbaikmu!

Nama Peserta :
Tanggal Tes :	Jumat, 4 April 2025
Jumlah Soal :	50 soal

Petunjuk Pengerjaan Soal:
Bentuk soal pilihan ganda, pilihlah jawaban yang benar di antara pilihan jawaban yang tersedia. Apabila Kamu merasa terdapat lebih dari satu jawaban yang benar, maka pilihlah yang paling benar.

1. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Rumus suku ke-$n$ suatu barisan adalah $U_{n}=3n+2$. Jumlah suku ke-$25$ dan suku ke-$27$ dari barisan tersebut adalah...

$(A)\ 154$

$(B)\ 160$

$(C)\ 164$

$(D)\ 166$

Alternatif Pembahasan:

Untuk barisan dengan suku ke-$n$ adalah $U_{n}=3n+2$, maka berlaku:
$\begin{align} U_{n} &= 3n+2 \\ U_{25} &= 3(25)+2=77 \\ U_{27} &= 3(27)+2=83 \\ \hline U_{25}+U_{27} &= 160 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 160$

2. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Peneliti $A$ dan $B$ mengembangbiakkan masing-masing $35$ amuba. Amuba Peneliti $A$ mampu membelah diri menjadi dua setiap $15$ menit sedangkan amuba Peneliti $B$ membelah diri menjadi dua setiap $25$ menit. Amuba peneliti $A$ saat ini menjadi $1.120$. Peneliti $B$ akan memiliki amuba saat ini sebanyak...

$(A)\ 135$

$(B)\ 192$

$(C)\ 256$

$(D)\ 280$

Alternatif Pembahasan:

Amuba peneliti $A$ saat ini sebanyak $1.120$ yang berawal dari $35$ amuba.
$35\underset{1\times}{\rightarrow}70\underset{2\times}{\rightarrow}140\underset{3\times}{\rightarrow}280\underset{4\times}{\rightarrow}560\underset{5\times}{\rightarrow}1120$
Dari skema di atas pembelahan amuba terjadi $5 \times$, dan waktu yang dibutuhkan adalah $5 \times 15 =75$ menit.

Untuk waktu selama $75$ menit amuba pada peneliti B yang membelah diri setiap $25$ menit akan membelah sebanyak $3 \times$,
$35\underset{1\times}{\rightarrow}70\underset{2\times}{\rightarrow}140\underset{3\times}{\rightarrow}280$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 280$

3. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap

Perhatikan pola yang dibentuk dari potongan lidi berikut ini!

Banyak potongan lidi pada pola ke-$55$ adalah...

$(A)\ 166$

$(B)\ 169$

$(C)\ 170$

$(D)\ 175$

Alternatif Pembahasan:

Dari gambar, dapat kita hitung banyak persegi dan lidi yang digunakan.
Pola (1)= ada 1 persegi dan 4 lidi,
Pola (2)= ada 2 persegi dan 7 lidi,
Pola (3)= ada 3 persegi dan 10 lidi,
Jika kita teruskan maka akan kita peroleh;
Pola (4)= ada 4 persegi dan 13 lidi,
Pola (5)= ada 5 segitiga dan 16 lidi,

Banyak lidi yang digunakan pada pola ke-$55$ adalah suku ke-$55$ dari barisan aritmatika berikut;
$4,\ 7,\ 10,\ 13,\ 16, \cdots$
$\begin{align} u_{n} & = a+(n-1)b \\ a & =4 \\ b & =7-4=3 \\ n & =55 \\ u_{55} & =4+(55-1)3 \\ & =4+162 \\ & =166 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 166$

4. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap

Jumlah bilangan kelipatan $3$ dan $4$ antara $200$ dan $300$ adalah...

$(A)\ 1.968$

$(B)\ 1.764$

$(C)\ 1.680$

$(D)\ 1.476$

Alternatif Pembahasan:

Kelipatan $3$ dan $4$ adalah bilangan kelipatan $12$.
Bilangan kelipatan $12$ antara $200$ dan $300$ adalah $204,\ 216,\ 228, \cdots ,288$
$204+216+228+ \cdots +288$
Suku ke-$n$ atau $u_{n}=288$, $a=204$ dan $b=12$
$\begin{align} u_{n} & = a+(n-1)b \\ 288 & = 204+(n-1)12 \\ 288 & = 204+12n-12 \\ 288-204+12 & = 12n \\ 96 & = 12n \\ n & = \frac{96}{12}=8 \end{align}$

Jumlah $16$ suku adalah $S_{8}$
$\begin{align} S_{n} & = \frac{n}{2} \left( a+u_{n} \right) \\ S_{8} & = \frac{8}{2} \left( 204+288 \right) \\ & = 4 \left( 492 \right) \\ & = 1.968 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 1.968$

5. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap

Tiga suku berikutnya dari barisan $4,\ 6,\ 10,\ 16,\ 24,\ \cdots$ adalah...

$(A)\ 32,\ 42,\ 54$

$(B)\ 34,\ 44,\ 56$

$(C)\ 34,\ 46,\ 60$

$(D)\ 32,\ 48,\ 80$

Alternatif Pembahasan:

Barisan bilangan $4,\ 6,\ 10,\ 16,\ \cdots$
dari $4$ ke $6$: $+2$
dari $6$ ke $10$: $+4$
dari $10$ ke $16$: $+6$
dari $16$ ke $24$: $+8$
jika kita teruskan pola pertambahan adalah $+10$, $+12$, $+14$ dan seterusnya.
bilangan setelah $24$ kita $+10$ hasilnya $34$;
bilangan setelah $34$ kita $+12$ hasilnya $36$;
bilangan setelah $36$ kita $+14$ hasilnya $60$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 34,\ 46,\ 60$

6. Soal UNBK Matematika SMP 2018 |*Soal Lengkap

Perhatikan pola yang dibentuk dari potongan lidi berikut ini!

Banyak potongan lidi pada pola ke (50) adalah...

$(A)\ 195$

$(B)\ 199$

$(C)\ 203$

$(D)\ 207$

Alternatif Pembahasan:

Dari gambar, dapat kita hitung banyak segitiga yang terbentuk dan lidi yang digunakan.
Pola (1)= ada 1 segitiga dan 3 lidi,
Pola (2)= ada 3 segitiga dan 7 lidi,
Pola (3)= ada 5 segitiga dan 11 lidi,
Jika kita teruskan maka akan kita peroleh;
Pola (4)= ada 7 segitiga dan 15 lidi,
Pola (5)= ada 9 segitiga dan 19 lidi,

Banyak lidi yang digunakan pada pola ke-$50$ adalah suku ke-$50$ dari barisan aritmatika berikut;
$3,\ 7,\ 11,\ 15,\ 19, \cdots$
$\begin{align} u_{n} & = a+(n-1)b \\ a & =3 \\ b & =7-3=4 \\ n & =50 \\ u_{50} & =3+(50-1)4 \\ & =3+(49)4 \\ & =3+196 \\ & =199 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 199$

7. Soal UNBK Matematika SMP 2018 |*Soal Lengkap

Jumlah bilangan kelipatan $2$ dan $3$ antara $200$ dan $400$ adalah...

$(A)\ 9.900$

$(B)\ 13.200$

$(C)\ 19.600$

$(D)\ 19.800$

Alternatif Pembahasan:

Kelipatan $2$ dan $3$ adalah bilangan kelipatan $6$.
Bilangan kelipatan $6$ antara $200$ dan $400$ adalah $204,\ 210,\ 216, \cdots ,396$
$204+210+216+ \cdots +396$
Suku ke-n atau $u_{n}=396$, $a=204$ dan $b=6$
$\begin{align} u_{n} & = a+(n-1)b \\ 396 & = 204+(n-1)6 \\ 396 & = 204+6n-6 \\ 396 & = 198+6n \\ 396-198 & = 6n \\ 198 & = 6n \\ n & = \frac{198}{6}=33 \end{align}$

Jumlah $33$ suku adalah $S_{33}$
$\begin{align} S_{n} & = \frac{n}{2} \left( a+u_{n} \right) \\ S_{33} & = \frac{33}{2} \left( 204+396 \right) \\ & = \frac{33}{2} \left( 600 \right) \\ & = 33 \times 300 \\ & = 9.900 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 9.900$

8. Soal UNBK Matematika SMP 2018 |*Soal Lengkap

Tiga suku berikutnya dari barisan $25,\ 27,\ 30,\ 34,\ \cdots$ adalah...

$(A)\ 39,\ 42,\ 46$

$(B)\ 38,\ 43,\ 49$

$(C)\ 39,\ 44,\ 49$

$(D)\ 39,\ 45,\ 52$

Alternatif Pembahasan:

Barisan bilangan $25,\ 27,\ 30,\ 34,\ \cdots$
dari $25$ ke $27$: $+2$
dari $27$ ke $30$: $+3$
dari $30$ ke $34$: $+4$
jika kita teruskan:
dari $34$ ke $39$: $+5$
dari $39$ ke $45$: $+6$
dari $45$ ke $52$: $+7$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 39,\ 45,\ 52$

9. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap

Perhatikan gambar berikut!

Gambar berpola di atas terbentuk dari beberapa persegi. banyak persegi pada gambar ke-7 adalah...

$(A)\ 21$

$(B)\ 25$

$(C)\ 29$

$(D)\ 46$

Alternatif Pembahasan:

Dengan memperhatikan gambar;

• gambar $(1)$ banyak persegi adalah 1.
• gambar $(2)$ banyak persegi adalah 5.
• gambar $(3)$ banyak persegi adalah 9.
$\vdots$
• gambar $(7)$ banyak persegi adalah $\cdots$

Banyak persegi untuk setiap gambar mempunyai pola dan aturan pola ini sepertinya sama dengan aturan pada Barisan aritmetika, dengan suku pertama $a=1$ dan $b=4$.

Gambar ke-n sama dengan suku yang ke-n;
$u_{n}=a+(n-1)b$

Gambar ke-7 sama dengan suku yang ke-7;
$u_{7}=1+(7-1)4$
$u_{7}=1+(6)4$
$u_{7}=25$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 25$

10. Soal UN Matematika SMP 2018 |*Soal Lengkap

Tiga suku berikutnya dari barisan $1,\ 5,\ 11,\ 19,\ \cdots$ adalah...

$(A)\ 29,\ 42,\ 56$

$(B)\ 29,\ 41,\ 55$

$(C)\ 29,\ 40,\ 49$

$(D)\ 29,\ 39,\ 49$

Alternatif Pembahasan:

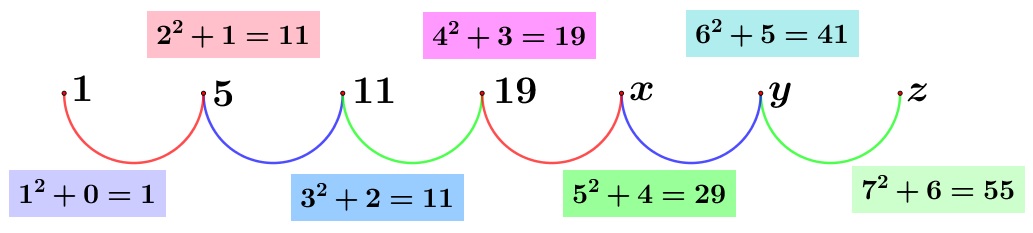
Barisan bilangan $1,\ 5,\ 11,\ 19,\ \cdots$ diperoleh dari:

• $1^{2}+0=1$
• $2^{2}+1=5$
• $3^{2}+2=11$
• $4^{2}+3=19$
• $5^{2}+4=29$
• $6^{2}+5=41$
• $7^{2}+6=55$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 29,\ 41,\ 55$

11. Soal UN Matematika SMP 2017 |*Soal Lengkap

Perhatikan barisan bilangan berikut: $12,\ 20,\ 30,\ 42,\ 56,\ \cdots$. Suku ke-12 dari barisan tersebut adalah...

$(A)\ 132$

$(B)\ 156$

$(C)\ 182$

$(D)\ 210$

Alternatif Pembahasan:

Barisan bilangan $12,\ 20,\ 30,\ 42,\ 56,\ \cdots$ diperoleh dari:

• $12= 4 \times 3$
• $20= 5 \times 4$
• $30= 6 \times 5$
• $42= 7 \times 6$
• $56= 8 \times 7$
• Suku ke-12 adalah: $\begin{align} (12+3) \times (12+2) &=15 \times 14 \\ &=210 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 210$

12. Soal Masuk Asrama YASOP - SMAN 2 Balige 2018 |*Soal Lengkap

Gambar berikut adalah segitiga yang disusun dari batang korek api. Banyak batang korek api yang dibutuhkan untuk membuat pola ke-6 adalah...

$(A)\ 36$

$(B)\ 48$

$(C)\ 63$

$(D)\ 84$

Alternatif Pembahasan:

Dari gambar diatas banyak korek api yang diperlukan pada setiap pola adalah:

• (1): $3=1 \times 3$
• (2): $9=(1+2) \times 3$
• (3): $18=(1+2+3) \times 3$
• (4): $30=(1+2+3+4) \times 3$
• (5): $(1+2+3+4+5) \times 3$
• (6): $(1+2+3+4+5+6) \times 3=63$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 63$

13. Soal Masuk Asrama YASOP - SMAN 2 Balige 2018 |*Soal Lengkap

Jumlah semua bilangan asli antara $20$ dan $140$ yang habis dibagi $3$ tetapi tidak habis dibagi $2$ adalah...

$(A)\ 1530$

$(B)\ 1540$

$(C)\ 1550$

$(D)\ 1560$

Alternatif Pembahasan:

Bilangan di antara $20$ dan $140$ yang habis dibagi $3$ adalah $21, 24, 27, \cdots , 135, 138$ ini adalah barisan aritmatika dengan $a=21$ dan $b=3$, maka jumlahnya adalah
$\begin{align} U_{n} & = a+(n-1)b \\ 138 & = 21+(n-1)3 \\ 138 & = 21+3n-3 \\ 138-18 & =3n \\ \dfrac{120}{3} & =n \\ 40 & =n \\ S_{n} & = \dfrac{}{} \left( a+U_{n}\right) \\ S_{40} & = \dfrac{40}{2} \left( 21+138 \right) \\ & = 20 \left( 159 \right) \\ & = 3180 \end{align}$

Bilangan di antara $20$ dan $140$ yang habis dibagi $3$ dan $2$ adalah $24, 30, \cdots , 132, 138$ ini adalah barisan aritmatika dengan $a=24$ dan $b=6$, maka jumlahnya adalah
$\begin{align} U_{n} & = a+(n-1)b \\ 138 & = 24+(n-1)6 \\ 138 & = 24+6n-6 \\ 138-18 & =6n \\ \dfrac{120}{6} & =n \\ 20 & =n \\ S_{n} & = \dfrac{n}{2} \left( a+U_{n}\right) \\ S_{20} & = \dfrac{20}{2} \left( 24+138 \right) \\ & = 10 \left( 162 \right) \\ & = 1620 \end{align}$
Jumlah bilangan yang habis dibagi $3$ tetapi tidak habis dibagi $2$ adalah $3180-1620=1560$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 1560$

14. Soal Masuk Asrama YASOP - SMAN 2 Balige 2009 |*Soal Lengkap

Lengkapi barisan berikut $3,\ 3,\ 9,\ 45,\ 315,\ \cdots$

$(A)\ 2538$

$(B)\ 2853$

$(C)\ 2385$

$(D)\ 2835$

Alternatif Pembahasan:

Barisan $3,\ 3,\ 9,\ 45,\ 315,\ \cdots$ memiliki pola yang tersembunyi dan harus ditemukan sendiri. Pola bilangan yang umum dipelajari adalah barisan aritmatika, sedangkan barisan ini tidak termasuk barisan aritmatika.

Untuk menemukan pola bilangan sangat dipengaruhi kecepatan dalam menghitung dan manipulasi alajabar dalam berhitung;

$\therefore$ Pilihan yang sesuai adalah $(D)\ 2835$

15. Soal Masuk Asrama YASOP - SMAN 2 Balige 2009 |*Soal Lengkap

Diberikan barisan $81,\ 2,\ 27,\ 6,\ 9,\ 18,\ a,\ b$. Nilai $b$ dan $a$ adalah...

$(A)\ 54\ \text{dan}\ 3$

$(B)\ 3\ \text{dan}\ 54$

$(C)\ 3\ \text{dan}\ 45$

$(D)\ 45\ \text{dan}\ 3$

Alternatif Pembahasan:

Barisan $81,\ 2,\ 27,\ 6,\ 9,\ 18,\ a,\ b$ memiliki pola yang tersembunyi dan harus ditemukan sendiri. Pola bilangan yang umum dipelajari adalah barisan aritmatika, sedangkan barisan ini tidak termasuk barisan aritmatika.

Untuk menemukan pola bilangan sangat dipengaruhi kecepatan dalam menghitung dan manipulasi alajabar dalam berhitung;

$\therefore$ Pilihan yang sesuai adalah $(A)\ 54\ \text{dan}\ 3$

16. Soal Masuk Asrama YASOP - SMAN 2 Balige 2008 |*Soal Lengkap

Lengkapi barisan berikut $3,\ 6,\ 12,\ 15,\ 30,\ 33,\ \cdots$

$(A)\ 36$

$(B)\ 66$

$(C)\ 99$

$(D)\ 38$

Alternatif Pembahasan:

Barisan $3,\ 6,\ 12,\ 15,\ 30,\ 33,\ \cdots$ memiliki pola yang tersembunyi dan harus ditemukan sendiri. Pola bilangan yang umum dipelajari adalah barisan aritmatika, sedangkan barisan ini tidak termasuk barisan aritmatika.

Untuk menemukan pola bilangan sangat dipengaruhi kecepatan dalam menghitung dan manipulasi alajabar dalam berhitung;

$\therefore$ Pilihan yang sesuai adalah $(B)\ 66$

17. Soal Masuk Asrama YASOP - SMAN 2 Balige 2008 |*Soal Lengkap

Lengkapi barisan berikut $3,\ 3,\ 6,\ 18,\ 72,\ 360,\ \cdots$

$(A)\ 2520$

$(B)\ 720$

$(C)\ 2160$

$(D)\ 1440$

Alternatif Pembahasan:

Barisan $3,\ 3,\ 6,\ 18,\ 72,\ 360,\ \cdots$ memiliki pola yang tersembunyi dan harus ditemukan sendiri. Pola bilangan yang umum dipelajari adalah barisan aritmatika, sedangkan barisan ini tidak termasuk barisan aritmatika.

Untuk menemukan pola bilangan sangat dipengaruhi kecepatan dalam menghitung dan manipulasi alajabar dalam berhitung;

$\therefore$ Pilihan yang sesuai adalah $(C)\ 2160$

18. Soal Masuk Asrama YASOP - SMAN 2 Balige 2008 |*Soal Lengkap

Berapakah nilai $a$ dan $b$ pada barisan berikut ini $2,\ 3,\ 4,\ 6,\ 8,\ 9,\ 16,\ a,\ b,$

$(A)\ 18\ \text{dan}\ 19$

$(B)\ 27\ \text{dan}\ 32$

$(C)\ 12\ \text{dan}\ 32$

$(D)\ 32\ \text{dan}\ 33$

Alternatif Pembahasan:

Barisan $2,\ 3,\ 4,\ 6,\ 8,\ 9,\ 16,\ a,\ b,$ memiliki pola yang tersembunyi dan harus ditemukan sendiri. Pola bilangan yang umum dipelajari adalah barisan aritmatika, sedangkan barisan ini tidak termasuk barisan aritmatika.

Untuk menemukan pola bilangan sangat dipengaruhi kecepatan dalam menghitung dan manipulasi alajabar dalam berhitung;

$\therefore$ Pilihan yang sesuai adalah $(C)\ 12\ \text{dan}\ 32$

19. Soal Masuk Asrama YASOP - SMAN 2 Balige 2009 |*Soal Lengkap

Suku ke-$n$ dari barisan $1,\ 3,\ 6,\ 10,\ 15,\ 21,\ \cdots$ adalah...

$(A)\ n(n+1)$

$(B)\ \dfrac{n(n+1)}{2}$

$(C)\ n(n+2)$

$(D)\ \dfrac{n(n+2)}{2}$

Alternatif Pembahasan:

Barisan $1,\ 3,\ 6,\ 10,\ 15,\ 21,\ \cdots$ barisan aritmatika tingkat dua;
jika kita manipulasi bentuknya menjadi
$u_{1}=\dfrac{1 \times 2}{2}=1$
$u_{2}=\dfrac{2 \times 3}{2}=3$
$u_{3}=\dfrac{3 \times 4}{2}=6$
$u_{4}=\dfrac{4 \times 5}{2}=10$
$\vdots$
$u_{2}=\dfrac{20 \times 21}{2}=210$
$u_{n}=\dfrac{n \times (n+1)}{2}=3$

$\therefore$ Pilihan yang sesuai adalah $(B)\ \dfrac{n(n+1)}{2}$

20. Soal Masuk Asrama YASOP - SMAN 2 Balige 2007 |*Soal Lengkap

Dari suatu barisan aritmatika diketahui $U_{3}=5$, $U_{7}=13$ dan $b=2$. Rumus suku ke-$n$ barisan bilangan tersebut adalah...

$(A)\ U_{n}=2n+1$

$(B)\ U_{n}=2n-1$

$(C)\ U_{n}=3n-1$

$(D)\ U_{n}=n^{2}-1$

Alternatif Pembahasan:

Pada soal disampaikan bahwa barisan aritmatika dimana $U_{3}=5$ maka $a+2b=5$ dan $U_{7}=13$ maka $a+6b=13$
Untuk $b=2$ dan $a+2b=5$ kita peroleh $a+2(2)=5$ atau $a=1$.

Suku ke-$n$ adalah...
$\begin{align} U_{n}& = a+(n-1)b \\ & = 1+(n-1)2 \\ & = 1+2n-2 \\ & = 2n-1 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ U_{n}=2n-1$

21. Soal Masuk Asrama YASOP - SMAN 2 Balige 2007 |*Soal Lengkap

Suku ke-$n$ dari barisan $1,\ 3,\ 6,\ 10,\ 15,\ 21,\ \cdots$ adalah...

$(A)\ n(n+1)$

$(B)\ \dfrac{n(n+1)}{2}$

$(C)\ n(n+2)$

$(D)\ \dfrac{n(n+2)}{2}$

Alternatif Pembahasan:

Barisan $1,\ 3,\ 6,\ 10,\ 15,\ 21,\ \cdots$ barisan aritmatika tingkat dua;
jika kita manipulasi bentuknya menjadi
$u_{1}=\dfrac{1 \times 2}{2}=1$
$u_{2}=\dfrac{2 \times 3}{2}=3$
$u_{3}=\dfrac{3 \times 4}{2}=6$
$u_{4}=\dfrac{4 \times 5}{2}=10$
$\vdots$
$u_{2}=\dfrac{20 \times 21}{2}=210$
$u_{n}=\dfrac{n \times (n+1)}{2}=3$

$\therefore$ Pilihan yang sesuai adalah $(B)\ \dfrac{n(n+1)}{2}$

22. Soal Masuk Asrama YASOP - SMAN 2 Balige 2007 |*Soal Lengkap

Rumus suku ke-$n$ dari barisan bilangan $0,\ 4,\ 10,\ 18,\ \cdots$ adalah...

$(A)\ \dfrac{1}{2}n(n+1)$

$(B)\ 2n(n+1)$

$(C)\ (n-1)(n+2)$

$(D)\ (n+1)(n+2)$

Alternatif Pembahasan:

Barisan $0,\ 4,\ 10,\ 18,\ \cdots$ barisan aritmatika tingkat dua;
jika kita manipulasi bentuknya menjadi
$u_{1}= 0 \times 1=0$
$u_{2}= 1 \times 4=4$
$u_{3}= 2 \times 5=10$
$u_{4}= 3 \times 6=18$
$u_{5}= 4 \times 7=28$
$\vdots$
$u_{20}=19 \times 22$
$u_{n}=(n-1) \times (n+2)$

$\therefore$ Pilihan yang sesuai adalah $(C)\ (n-1) (n+2)$

23. Soal Masuk Asrama YASOP - SMAN 2 Balige 2006 |*Soal Lengkap

Suatu barisan bilangan $2,\ 6,\ 12,\ 20,\ \cdots$ suku yang ke-20 adalah...

$(A)\ 420$

$(B)\ 480$

$(C)\ 500$

$(D)\ 602$

Alternatif Pembahasan:

Barisan $2,\ 6,\ 12,\ 20,\ \cdots$ barisan aritmatika tingkat dua;
jika kita manipulasi bentuknya menjadi
$u_{1}=1 \times 2$
$u_{2}=2 \times 3$
$u_{3}=3 \times 4$
$u_{4}=4 \times 5$
$\vdots$
$u_{20}=20 \times 21=420$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 420$

24. Soal Masuk Asrama YASOP - SMAN 2 Balige 2005 |*Soal Lengkap

Bilangan-bilangan disusun dan dikelompokkan menurut pola:
$(2,6),\ (3,7), (4,8), (5,9), \cdots$ dan seterusnya.
Bilangan pada kelompok ke-62 adalah...

$(A)\ (61,65)$

$(B)\ (62,66)$

$(C)\ (63,67)$

$(D)\ (64,68)$

Alternatif Pembahasan:

Dari pola bilangan yang diketahui $(2,6),\ (3,7),\ (4,8)\, (5,9), \cdots$ kita peroleh
$k_{1}=(2,6)$
$k_{2}=(3,7)$
$k_{3}=(4,8)$
$k_{4}=(5,9)$
$\vdots$
$k_{n}=(n+1,5+n)$
$k_{62}=(63,67)$

$\therefore$ Pilihan yang sesuai adalah $(C)\ (63,67)$

25. Soal Masuk SMA Unggul Del 2018 |*Soal Lengkap

Perhatikan pola berikut:

Banyak lingkaran pada pola ke-50 adalah...

$(A)\ 1275$

$(B)\ 1326$

$(C)\ 1452$

$(D)\ 1546$

Alternatif Pembahasan:

Dari gambar dapat kita ambil beberapa informasi, yaitu:

• banyak lingkaran pada pola $[1]=3=1+2$; ekuivalen dengan $S_{2}$ pada deret aritmatika dimana $a=1$; $b=1$; $n=2$
• banyak lingkaran pada pola $[2]=6=1+2+3$; ekuivalen dengan $S_{3}$ pada deret aritmatika dimana $a=1$; $b=1$; $n=3$
• banyak lingkaran pada pola $[3]=10=1+2+3+4$; ekuivalen dengan $S_{4}$ pada deret aritmatika dimana $a=1$; $b=1$; $n=4$
• banyak lingkaran pada pola $[4]=15=1+2+3+4+5$; ekuivalen dengan $S_{5}$ pada deret aritmatika dimana $a=1$; $b=1$; $n=5$

Dengan melihat pola banyak lingkaran diatas, pola ini disebut dengan pola bilangan segitiga, dimana pola bilangan juga mengikuti aturan barisan dan deret aritmatika.

Banyak lingkaran pola ke-50 sama dengan $S_{51}$ pada deret aritmatika dimana $a=1$; $b=1$; $n=51$;
$\begin{align} S_{n} &= \dfrac{n}{2} \left( 2a +(n-1)b \right) \\ S_{51} &= \dfrac{51}{2} \left( 2(1) +(51-1)1 \right) \\ &= \dfrac{51}{2} \left( 2 +(50) \right) \\ &= \dfrac{51}{2} (52) \\ &= 1326 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 1326$

26. Soal UN Matematika SMP 2018 |*Soal Lengkap

Jika pola di atas dilanjutkan, banyak bulatan pada pola ke-61 adalah...

$(A)\ 249$

$(B)\ 241$

$(C)\ 66$

$(D)\ 64$

Alternatif Pembahasan:

Dari gambar, dapat kita hitung banyak bulatan yang terbetuk adalah:
Pola (1)= ada 1 bulatan,
Pola (2)= ada 5 bulatan,
Pola (3)= ada 9 bulatan,
Jika kita teruskan maka akan kita peroleh;
Pola (4)= ada 13 bulatan,
Pola (5)= ada 17 bulatan,

Dari pola di atas, banyak bulatan membentuk pola barisan aritmetika karena bulatan selalu bertambah $4$, Banyak bulatan pola ke-61 adalah:
$1,\ 5,\ 9,\ 13,\ \cdots$
$\begin{align} u_{n} & = a+(n-1)b \\ a & =1 \\ b & =5-1=4 \\ n & =61 \\ u_{61} & =1+(61-1)4 \\ & =1+(60)4 \\ & =1+240 \\ & =241 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 241$

27. Soal UN Matematika SMP 2018 |*Soal Lengkap

Jumlah semua bilangan kelipatan $3$ dan $4$ antara $200$ dan $450$ adalah...

$(A)\ 8.700$

$(B)\ 6.804$

$(C)\ 6.360$

$(D)\ 6.300$

Alternatif Pembahasan:

Kelipatan $3$ dan $4$ adalah bilangan kelipatan $12$.
Bilangan kelipatan $12$ antara $200$ dan $450$ adalah $204,\ 216,\ 228, \cdots ,444$
$204+216+228+ \cdots +444$
Suku ke-n atau $u_{n}=444$, $a=204$ dan $b=12$
$\begin{align} u_{n} & = a+(n-1)b \\ 444 & = 204+(n-1)12 \\ 444 & = 204+12n-12 \\ 444-204+12 & = 12n \\ 252 & = 12n \\ n & = \frac{252}{12}=21 \end{align}$

Jumlah $21$ suku adalah $S_{21}$
$\begin{align} S_{n} & = \frac{n}{2} \left( a+u_{n} \right) \\ S_{21} & = \frac{21}{2} \left( 204+444 \right) \\ & = \frac{21}{2} \left( 648 \right) \\ & = 21 \times 324 = 6.804 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 6.804$

28. Soal UN Matematika SMP 2016 |*Soal Lengkap

Gambar berikut adalah segitiga yang disusun dari batang korek api.

Banyak batang korek api yang diperlukan untuk membuat pola ke-7 adalah...

$(A)\ 45$

$(B)\ 63$

$(C)\ 84$

$(D)\ 108$

Alternatif Pembahasan:

Dari gambar diatas banyak korek api yang diperlukan pada setiap pola adalah:

• (1): $3=1 \times 3$
• (2): $9=(1+2) \times 3$
• (3): $18=(1+2+3) \times 3$
• (4): $30=(1+2+3+4) \times 3$
• (5): $(1+2+3+4+5) \times 3$
  $\vdots$
• (7): $(1+2+3+4+5+6+7) \times 3$
  $\dfrac{7}{2} \left(1+7 \right) \times 3 =84$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 84$

29. Soal UN Matematika SMP 2016 |*Soal Lengkap

Suku pertama dan kelima suatu barisan geometri berturut-turut $5$ dan $80$. Suku ke-9 barisan tersebut adalah...

$(A)\ 90$

$(B)\ 405$

$(C)\ 940$

$(D)\ 1.280$

Alternatif Pembahasan:

Barisan Bilangan Geometri $a,\ a \cdot r^{1},\ a \cdot r^{2},\ a\cdot r^{3},\ \cdots$
Suku ke-$n$: $U_{n}= a \cdot r^{n-1}$
$\begin{align} U_{n} &= a \cdot r^{n-1} \\ U_{5} &= 5 \cdot r^{5-1} \\ 80 &= 5 \cdot r^{4} \\ 16 &= r^{4} \longrightarrow r=2 \\ \hline U_{n} &= a \cdot r^{n-1} \\ U_{9} &= 5 \cdot 2^{9-1} \\ &= 5 \cdot 2^{8} \\ &= 5 \cdot 256 = 1.028 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 1.028$

30. Soal UN Matematika SMP 2016 |*Soal Lengkap

Seutas tali dipotong menjadi $5$ bagian sehingga ukurannya membentuk deret geometri. Jika panjang potongan tali terpendek $4\ cm$ dan potongan tali terpanjang $324\ cm$, maka panjang tali semula adalah...

$(A)\ 328\ cm$

$(B)\ 484\ cm$

$(C)\ 648\ cm$

$(D)\ 820\ cm$

Alternatif Pembahasan:

Barisan Bilangan Geometri $a,\ a \cdot r^{1},\ a \cdot r^{2},\ a\cdot r^{3},\ \cdots$
Suku ke-$n$: $U_{n}= a \cdot r^{n-1}$
Jumlah $n$ suku pertama $S_{n} = \dfrac{ a \left( r^{n} - 1 \right)}{\left(r-1 \right)},\ \text{dengan}\ r \neq 1$

dari informasi pada soal kita peroleh banyak potongan $n=5$ sehingga yang terpendek $a=4$ dan yang terpanjang $U_{5} = 324$.

$\begin{align} U_{n} &= a \cdot r^{n-1} \\ U_{5} &= 4 \cdot r^{5-1} \\ 324 &= 4 \cdot r^{4} \\ 81 &= r^{4} \longrightarrow r= 3 \\ \hline S_{n} &= \dfrac{ a \left( r^{n} - 1 \right)}{\left(r-1 \right)} \\ S_{5} &= \dfrac{ 4 \left( 3^{5} - 1 \right)}{\left(3-1 \right)} \\ &= \dfrac{ 4 \left( 243 - 1 \right)}{2} \\ &= 2 \left( 242 \right) = 484 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 484$

31. Soal UN Matematika SMP 2015 |*Soal Lengkap

Seutas tali dipotong menjadi $5$ bagian dengan panjang masing-masing bagian membentuk barisan geometri. Jika potongan tali yang terpendek $5\ cm$ dan potongan tali terpanjang $80\ cm$, maka panjang tali semula adalah...

$(A)\ 170\ m$

$(B)\ 165\ m$

$(C)\ 160\ m$

$(D)\ 155\ m$

Alternatif Pembahasan:

Barisan Bilangan Geometri $a,\ a \cdot r^{1},\ a \cdot r^{2},\ a\cdot r^{3},\ \cdots$
Suku ke-$n$: $U_{n}= a \cdot r^{n-1}$
Jumlah $n$ suku pertama $S_{n} = \dfrac{ a \left( r^{n} - 1 \right)}{\left(r-1 \right)},\ \text{dengan}\ r \neq 1$

dari informasi pada soal kita peroleh banyak potongan $n=5$ sehingga yang terpendek $a=5$ dan yang terpanjang $U_{5} = 80$.

$\begin{align} U_{n} &= a \cdot r^{n-1} \\ U_{5} &= 5 \cdot r^{5-1} \\ 80 &= 5 \cdot r^{4} \\ 16 &= r^{4} \longrightarrow r= 2 \\ \hline S_{n} &= \dfrac{ a \left( r^{n} - 1 \right)}{\left(r-1 \right)} \\ S_{5} &= \dfrac{ 5 \left( 2^{5} - 1 \right)}{\left(2-1 \right)} \\ &= \dfrac{ 5 \left( 32 - 1 \right)}{1} \\ &= 5 \left( 31 \right) = 155 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 155$

32. Soal UN Matematika SMP 2015 |*Soal Lengkap

Jumlah bilangan kelipatan $3$ antara $200$ dan $400$ adalah...

$(A)\ 19.500$

$(B)\ 20.100$

$(C)\ 30.360$

$(D)\ 40.200$

Alternatif Pembahasan:

Bilangan kelipatan $3$ antara $200$ dan $400$ adalah $201,\ 204,\ 207, \cdots ,399$
$201+204+207+ \cdots +399$
Suku ke-n atau $u_{n}=399$, $a=201$ dan $b=3$
$\begin{align} u_{n} & = a+(n-1)b \\ 399 & = 201+(n-1)3 \\ 399 & = 201+3n-3 \\ 399-201+3 & = 3n \\ 201 & = 3n \\ n & = \dfrac{201}{3}=67 \end{align}$

Jumlah $67$ suku adalah $S_{67}$
$\begin{align} S_{n} & = \frac{n}{2} \left( a+u_{n} \right) \\ S_{67} & = \frac{67}{2} \left( 201+399 \right) \\ & = \frac{67}{2} \left( 600 \right) \\ & = 67 \times 300 = 20.100 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 20.100$

33. Soal UN Matematika SMP 2015 |*Soal Lengkap

Diketahui barisan bilangan $3,\ 8,\ 13,\ 18,\ 23, \cdots$
Suku ke-32 adalah...

$(A)\ 465$

$(B)\ 168$

$(C)\ 158$

$(D)\ 153$

Alternatif Pembahasan:

Barisan bilangan $3,\ 8,\ 13,\ 18,\ 23, \cdots$ membentuk barisan aritmatika karena bilangan naik dengan bertambah $5$.

$\begin{align} u_{n} & = a+(n-1)b \\ u_{32} & = 3+(32-1)5 \\ & = 3+(33)(5) \\ & = 3+ 165 \\ & = 168 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 168$

34. Soal UN Matematika SMP 2014 |*Soal Lengkap

Suku ketiga dan suku kelima barisan aritmetika adalah $17$ dan $31$. Suku ke-$20$ dari barisan tersebut adalah...

$(A)\ 136$

$(B)\ 168$

$(C)\ 158$

$(D)\ 153$

Alternatif Pembahasan:

Untuk barisan bilangan barisan aritmetika berlaku suku ke-$n$ $U_{n}= a+\left( n-1 \right)$ dan jumlah $n$ suku pertama $S_{n} = \dfrac{n}{2} \left( 2a+(n-1)b \right)$.

$\begin{align} u_{n} & = a+(n-1)b \\ u_{3} & = a+(3-1)b \\ 17 & = a+2b \\ \hline u_{5} & = a+(5-1)b \\ 31 & = a+4b \\ 31 & = a+2b+2b \\ 31 & = 17+2b \\ 14 & = 2b \longrightarrow b=\dfrac{14}{2}=7 \\ \hline 17 & = a+2b \\ 17 & = a+2(7) \\ 17 & = a+14 \longrightarrow a=3 \\ \hline u_{n} & = a+(n-1)b \\ u_{20} & = 3+(20-1)7 \\ & = 3+(19)7 \\ & = 3+133=136 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 136$

35. Soal UN Matematika SMP 2014 |*Soal Lengkap

Dari barisan aritmetika diketahui $u_{3}=18$ dan $u_{7}=38$. Jumlah $24$ suku pertama adalah...

$(A)\ 786$

$(B)\ 1.248$

$(C)\ 1.572$

$(D)\ 3.144$

Alternatif Pembahasan:

Untuk barisan bilangan barisan aritmetika berlaku suku ke-$n$ $U_{n}= a+\left( n-1 \right)$ dan jumlah $n$ suku pertama $S_{n} = \dfrac{n}{2} \left( 2a+(n-1)b \right)$.

$\begin{align} u_{n} & = a+(n-1)b \\ u_{3} & = a+(3-1)b \\ 18 & = a+2b \\ \hline u_{7} & = a+(7-1)b \\ 38 & = a+6b \\ 38 & = a+2b+4b \\ 38 & = 18+4b \\ 20 & = 4b \longrightarrow b=\dfrac{20}{4}=5 \\ \hline 18 & = a+2b \\ 18 & = a+2(5) \\ 18 & = a+10 \longrightarrow a=8 \\ \hline S_{n} & = \dfrac{n}{2} \left(2a+(n-1)b \right) \\ S_{24} & = \dfrac{24}{2} \left(2(8)+(24-1)(5) \right) \\ & = 12 \left(16+(23)(5) \right) \\ & = 12 \left( 16+115 \right) \\ & = 12 \left( 131 \right) =1.572 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 1.572$

36. Soal UN Matematika SMP 2014 |*Soal Lengkap

Banyak kursi pada baris pertama sebuah gedung pertunjukan adalah $20$ kursi, baris kedua $23$ kursi, dan seterusnya sehingga banyak kursi baris berikutnya selalu bertambah $3$ kursi. Jika dalam gedung tersebut terdapat $20$ baris kursi, maka jumlah kursi pada gedung tersebut adalah...

$(A)\ 270\ \text{kursi}$

$(B)\ 970\ \text{kursi}$

$(C)\ 1.000\ \text{kursi}$

$(D)\ 1.003\ \text{kursi}$

Alternatif Pembahasan:

Barisan kursi dalam gedung membentuk barisan bilangan barisan aritmetika karena beda setiap baris kursi tetap yaitu $3$. Sehingga banyak kursi keseluruhan dapat kita gunakan $S_{n}$ dari barisan aritmetika.

$\begin{align} S_{n} & = \dfrac{n}{2} \left(2a+(n-1)b \right) \\ S_{20} & = \dfrac{20}{2} \left(2(20)+(20-1)(3) \right) \\ & = 10 \left(40+(19)(3) \right) \\ & = 10 \left(40+57 \right) \\ & = 10 \left( 97 \right) =970 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 970$

37. Soal UN Matematika SMP 2013 |*Soal Lengkap

Suku ke-$48$ dari barisan bilangan $3,\ 10,\ 17,\ 24,\ 31,\ \cdots$ adalah...

$(A)\ 147$

$(B)\ 151$

$(C)\ 332$

$(D)\ 336$

Alternatif Pembahasan:

Barisan bilangan $3,\ 10,\ 17,\ 24,\ 31,\ \cdots$ membentuk barisan aritmatika karena bilangan naik dengan bertambah $7$.

$\begin{align} u_{n} & = a+(n-1)b \\ u_{48} & = 3+(48-1)7 \\ & = 3+(47)(7) \\ & = 3+ 329 \\ & = 332 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 332$

38. Soal UN Matematika SMP 2013 |*Soal Lengkap

Rumus suku ke-$n$ dari barisan bilangan $\dfrac{1}{2},\ 1,\ 2,\ 4,\ 8,\ \cdots$ adalah...

$(A)\ 2^{n+1}$

$(B)\ 2^{n}$

$(C)\ 2^{n-1}$

$(D)\ 2^{n-2}$

Alternatif Pembahasan:

Barisan bilangan $\dfrac{1}{2},\ 1,\ 2,\ 4,\ 8,\ \cdots$ membentuk barisan barisan aritmatika karena rasio bilangan selalu sama yaitu $\dfrac{u_{2}}{u_{1}}=\dfrac{u_{3}}{u_{2}}=2$.

Suku ke-$n$ adalah...
$\begin{align} U_{n} &= a \cdot r^{n-1} \\ U_{n} &= \dfrac{1}{2} \cdot 2^{n-1} \\ &= \dfrac{1}{2} \cdot 2^{n-1} \\ &= 2^{-1} \cdot 2^{n-1} \\ &= 2^{n-1-1} \\ &= 2^{n-2} \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(E)\ 2^{n-2}$

39. Soal UN Matematika SMP 2013 |*Soal Lengkap

Suatu barisan aritmetika suku ke-$2$ dan suku ke-$5$ masing-masing $19$ dan $31$. Jumlah $30$ suku pertama adalah...

$(A)\ 2.280$

$(B)\ 2.190$

$(C)\ 1.815$

$(D)\ 364$

Alternatif Pembahasan:

Untuk barisan bilangan barisan aritmetika berlaku suku ke-$n$ $U_{n}= a+\left( n-1 \right)$ dan jumlah $n$ suku pertama $S_{n} = \dfrac{n}{2} \left( 2a+(n-1)b \right)$.

$\begin{align} u_{n} & = a+(n-1)b \\ u_{2} & = a+(2-1)b \\ 19 & = a+ b \\ \hline u_{5} & = a+(5-1)b \\ 31 & = a+4b \\ 31 & = a+b+3b \\ 31 & = 19+3b \\ 12 & = 3b \longrightarrow b=\dfrac{12}{3}=4 \\ \hline 19 & = a+ b \\ 19 & = a+ 4 \longrightarrow a=15 \\ \hline S_{n} & = \dfrac{n}{2} \left(2a+(n-1)b \right) \\ S_{30} & = \dfrac{30}{2} \left(2(15)+(30-1)(4) \right) \\ & = 15 \left(30+(29)(4) \right) \\ & = 15 \left(30+ 116 \right) \\ & = 15 \left( 146 \right) =2.190 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 2.190$

40. Soal UN Matematika SMP 2012 |*Soal Lengkap

Dua suku berikutnya dari barisan $3,\ 4,\ 6,\ 9,\ \cdots$ adalah...

$(A)\ 13,\ 18$

$(B)\ 13,\ 17$

$(C)\ 12,\ 26$

$(D)\ 12,\ 15$

Alternatif Pembahasan:

Barisan $3,\ 4,\ 6,\ 9,\ \cdots$ barisan aritmatika tingkat dua. Untuk mendapatkan dua suku berikutnya dapat kita gunakan pola yang berlaku.

$\therefore$ Pilihan yang sesuai adalah $(A)\ 13,\ 18$

41. Soal UN Matematika SMP 2012 |*Soal Lengkap

Dari barisan aritmetika diketahui suku ke-$7$ adalah $22$ dan suku ke-$11$ adalah $34$. Jumlah $18$ suku pertama adalah...

$(A)\ 531$

$(B)\ 666$

$(C)\ 1062$

$(D)\ 1332$

Alternatif Pembahasan:

Untuk barisan bilangan barisan aritmetika berlaku suku ke-$n$ $U_{n}= a+\left( n-1 \right)$ dan jumlah $n$ suku pertama $S_{n} = \dfrac{n}{2} \left( 2a+(n-1)b \right)$.

$\begin{align} u_{n} & = a+(n-1)b \\ u_{7} & = a+(7-1)b \\ 22 & = a+ 6b \\ \hline u_{11} & = a+(11-1)b \\ 34 & = a+10b \\ 34 & = a+6b+4b \\ 34 & = 22+4b \\ 12 & = 4b \longrightarrow b=\dfrac{12}{4}=3 \\ \hline 22 & = a+ 6b \\ 22 & = a+ 6(3) \\ 22 & = a+ 18 \longrightarrow a=4 \\ \hline S_{n} & = \dfrac{n}{2} \left(2a+(n-1)b \right) \\ S_{18} & = \dfrac{18}{2} \left(2(4)+(18-1)(3) \right) \\ & = 9 \left(8+(17)(3) \right) \\ & = 9 \left(8+ 51 \right) \\ & = 9 \left( 59 \right) =531 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(A)\ 531$

42. Soal UN Matematika SMP 2012 |*Soal Lengkap

Bakteri akan membelah diri menjadi dua setiap $30$ menit. Jika mula-mula ada $25$ bakteri, maka banyaknya bakteri selama $4$ jam adalah...

$(A)\ 3.000$

$(B)\ 3.200$

$(C)\ 6.000$

$(D)\ 6.400$

Alternatif Pembahasan:

Bakteri akan membelah jadi dua setiap $30$ menit yang mula-mula $25$ bakteri.

Jika menggunakan aturan pada barisan geometri dapat kita gunakan suku pertama $a=25$, rasio $r=2$ dan banyak suku adalah $u_{1}$ ditambah $\dfrac{4 \text{jam}}{30 \text{menit}}=8$ sehingga total suku adalah $9$.

$\begin{align} U_{n} &= a \cdot r^{n-1} \\ U_{9} &= 25 \cdot 2^{9-1} \\ &= 25 \cdot 2^{8} \\ &= 25 \cdot 256 \\ &= 6.400 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 6.400$

43. Soal UN Matematika SMP 2011 |*Soal Lengkap

Diketahui $U_{n}=2n^{2}-5$. Nilai dari $U_{4}+U_{5}$ adalah...

$(A)\ 154$

$(B)\ 82$

$(C)\ 72$

$(D)\ 26$

Alternatif Pembahasan:

Untuk barisan dengan suku ke-$n$ adalah $U_{n}=2n^{2}-5$, maka berlaku:
$\begin{align} U_{n} &= 2n^{2}-5 \\ U_{4} &= 2(4)^{2}-5=27 \\ U_{5} &= 2(5)^{2}-5=45 \\ \hline U_{4}+U_{5} &= 72 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 72$

44. Soal UN Matematika SMP 2011 |*Soal Lengkap

Dua suku berikutnya dari barisan $1,\ 3,\ 7,\ 13,\ \cdots$ adalah...

$(A)\ 21\ \text{dan}\ 31$

$(B)\ 19\ \text{dan}\ 27$

$(C)\ 19\ \text{dan}\ 25$

$(D)\ 17\ \text{dan}\ 23$

Alternatif Pembahasan:

Barisan $1,\ 3,\ 7,\ 13,\ \cdots$ barisan aritmatika tingkat dua. Untuk mendapatkan dua suku berikutnya dapat kita gunakan pola yang berlaku.

$\therefore$ Pilihan yang sesuai adalah $(A)\ 21\ \text{dan}\ 31$

45. Soal TUK Masuk SMA Unggul DEL 2022 |*Soal Lengkap

Satu pasukan parade drum band yang berjumlah $49$ orang membentuk formasi barisan. Paling depan $1$ orang, kemudian dibelakangnya bertambah $2$, dan berikutnya bertambah $2$ lagi dan seterusnya. Maka banyaknya orang pada barisan terakhir adalah...

$(A)\ 11$

$(B)\ 13$

$(C)\ 15$

$(D)\ 17$

Alternatif Pembahasan:

Berdasarkan informasi pada soal pertambahan orang pada baris berikutnya selelu tetap, sehingga pertambahan orang setiap baris pasukan parade drum band ini sama dengan konsep arimetika. Dimana suku pertama $a=1$ dan $b=2$.

Jumlah seluruh siswa adalah $S_{n}=49$
$\begin{align} S_{n} & = \dfrac{n}{2} \left( 2a+ \left(n-1 \right)b \right) \\ 49 & = \dfrac{n}{2} \left( 2(1)+ \left(n-1 \right)(2) \right) \\ 49 & = \dfrac{n}{2} \left( 2+ 2n-2 \right) \\ 49 & = \dfrac{n}{2} \left( 2n \right) \\ 49 & = n^{2}\ \longrightarrow n=7 \end{align}$

Banyak suku atau banyak barisan adalah $7$, sehingga kita peroleh:
$\begin{align} u_{n} & = a+(n-1)b \\ u_{7} & = 1+(7-1)(2) \\ & = 1+ (6)(2) \\ & = 13 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 13$

46. Soal US-UM Matematika SMP |*Soal Lengkap

Diketahui deret arimetika dengan nilai suku ke-6 adalah $35$ dan suku ke-9 adalah $26$. Jumlah $25$ suku pertama deret arimetika tersebut adalah...

$(A)\ 275$

$(B)\ 312$

$(C)\ 350$

$(D)\ 396$

Alternatif Pembahasan:

Pada soal disampaikan bahwa barisan aritmatika dimana $U_{6}=35$ maka $a+5b=35$ dan $U_{9}=26$ maka $a+8b=26$
Dari kedua persamaan di atas dapat kita peroleh:
$\begin{align} a+5b & = 35 \\ a+8b & = 26\ \ (-) \\ \hline -3b & = 9 \\ b & = -3 \\ a+5(-3) & = 35\ \longrightarrow a=50 \end{align}$

Jumlah $25$ suku pertama deret aritmetika tersebut adalah:
$\begin{align} S_{n} & = \dfrac{n}{2} \left( 2a+ (n-1)b \right) \\ S_{25} & = \dfrac{25}{2} \left( 2(50)+ (25-1)(-3) \right) \\ S_{25} & = \dfrac{25}{2} \left( 100+ (24)(-3) \right) \\ S_{25} & = \dfrac{25}{2} \left( 100-72 \right) \\ S_{25} & = \dfrac{25}{2} \left( 28 \right) \\ S_{25} & = (25) \left( 14 \right) = 350 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 350$

47. Soal US-UM Matematika SMP |*Soal Lengkap

Suku ke-$4$ dan suku ke-$9$ suatu barisan aritmetika berturut-turut adalah $110$ dan $150$. Suku ke-$30$ barisan tersebut adalah...

$(A)\ 308$

$(B)\ 318$

$(C)\ 326$

$(D)\ 344$

Alternatif Pembahasan:

Untuk barisan bilangan barisan aritmetika berlaku suku ke-$n$ $U_{n}= a+\left( n-1 \right)$ dan jumlah $n$ suku pertama $S_{n} = \dfrac{n}{2} \left( 2a+(n-1)b \right)$.

$\begin{align} u_{n} & = a+(n-1)b \\ u_{4} & = a+(4-1)b \\ 110 & = a+3b \\ \hline u_{9} & = a+(9-1)b \\ 150 & = a+8b \\ 150 & = a+3b+5b \\ 150 & = 110+5b \\ 40 & = 5b \longrightarrow b=\dfrac{40}{5}=8 \\ \hline 110 & = a+3b \\ 110 & = a+3(8) \\ 110 & = a+24 \longrightarrow a=86 \\ \hline u_{n} & = a+(n-1)b \\ u_{30} & = 86+(30-1)8 \\ & = 86+(29)8 \\ & = 86+232=318 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 318$

48. Soal US-UM Matematika SMP |*Soal Lengkap

Dari barisan geomteri diketahui bahwa $u_{3}=4$ dan $u_{3}=256$, maka $u_{12}$ adalah...

$(A)\ 2049$

$(B)\ 2048$

$(C)\ 2047$

$(D)\ 2046$

Alternatif Pembahasan:

Untuk barisan bilangan barisan geometri berlaku suku ke-$n$ $u_{n}= ar^{n-1}$ dimana $a$ adalah suku pertama dan $r$ adalah rasio.

$\begin{align} u_{n} & = ar^{n-1} \\ u_{3} & = ar^{3-1} \\ 4 & = ar^{2} \\ \hline u_{9} & = ar^{9-1} \\ 256 & = ar^{8} \\ 256 & = ar^{2} \cdot r^{6} 256 & = 4 \cdot r^{6} \\ \dfrac{256}{4} & = r^{6} \\ 64 & = r^{6} \longrightarrow r=2 \\ \hline ar^{2} & = 4 \\ a \cdot 4 & = 4 \longrightarrow a=1 \\ \hline u_{n} & = ar^{n-1} \\ u_{12} & = ar^{12-1} \\ & = 1 \cdot 2^{11} \\ & = 2048 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 2048$

49. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Rumus suku ke-$n$ suatu barisan adalah $U_{n}=3n+2$. Jumlah suku ke-$25$ dan suku ke-$27$ dari barisan tersebut adalah...

$(A)\ 154$

$(B)\ 160$

$(C)\ 164$

$(D)\ 166$

Alternatif Pembahasan:

Untuk barisan dengan suku ke-$n$ adalah $U_{n}=3n+2$, maka berlaku:
$\begin{align} U_{n} &= 3n+2 \\ U_{25} &= 3(25)+2=77 \\ U_{27} &= 3(27)+2=83 \\ \hline U_{25}+U_{27} &= 160 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 160$

50. Soal UNBK Matematika SMP 2019 |*Soal Lengkap

Peneliti $A$ dan $B$ mengembangbiakkan masing-masing $35$ amuba. Amuba Peneliti $A$ mampu membelah diri menjadi dua setiap $15$ menit sedangkan amuba Peneliti $B$ membelah diri menjadi dua setiap $25$ menit. Amuba peneliti $A$ saat ini menjadi $1.120$. Peneliti $B$ akan memiliki amuba saat ini sebanyak...

$(A)\ 135$

$(B)\ 192$

$(C)\ 256$

$(D)\ 280$

Alternatif Pembahasan:

Amuba peneliti $A$ saat ini sebanyak $1.120$ yang berawal dari $35$ amuba.
$35\underset{1\times}{\rightarrow}70\underset{2\times}{\rightarrow}140\underset{3\times}{\rightarrow}280\underset{4\times}{\rightarrow}560\underset{5\times}{\rightarrow}1120$
Dari skema di atas pembelahan amuba terjadi $5 \times$, dan waktu yang dibutuhkan adalah $5 \times 15 =75$ menit.

Untuk waktu selama $75$ menit amuba pada peneliti B yang membelah diri setiap $25$ menit akan membelah sebanyak $3 \times$,
$35\underset{1\times}{\rightarrow}70\underset{2\times}{\rightarrow}140\underset{3\times}{\rightarrow}280$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 280$

Catatan Pembahasan Soal Pola, Barisan, dan Deret Bilangan Matematika SMP di atas sifatnya "dokumen hidup" yang senantiasa diperbaiki atau diperbaharui sesuai dengan dinamika kebutuhan dan perubahan zaman. Catatan tambahan dari Anda untuk admin diharapkan dapat meningkatkan kualitas catatan ini 🙏 CMIIW.

JADIKAN HARI INI LUAR BIASA!
Ayo Share (Berbagi) Satu Hal Baik.

Jangan jadikan sekolah hanya untuk mencari nilai, tetapi bagaimana sekolah itu menjadikanmu bernilai.

Pythagoras